1. 引言
本文研究如下静电磁Schrödinger-Maxwell系统
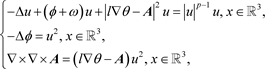 (1)
(1)
涡旋基态解的存在性,其中
和
。
在1998年,Benci和Fortunato在 [6] 中介绍了如下系统
(2)
在 [1] [2] 和 [3] 中,选取
系统(2)退化为如下Schrödinger-Poisson系统
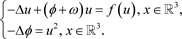 (3)
(3)
在过去的几十年里,许多学者对系统(3)或其更一般形式的基态、束缚态、变号解的存在性和多重性进行了大量的研究,在这里我们就不再一一列举。感兴趣的读者可以参考文献 [4] - [10] 及它们的参考文献。
在2009年,Benci和Fortunato在 [7] 中研究如下的Klein-Gordon-Maxwell系统
(4)
系统(4)可能有三种类型解:静电解:
;静磁解:
和静电磁解:
。选取
其中
(5)
易得,
,
。
于是系统(4)退化为如下系统
 (6)
(6)
在 [11] 中Benci和Fortunato利用山路引理证明了系统(6)解的存在性。
在2017年,Avenia等人在 [12] 中考虑了如下的静电磁Klein-Gordon-Maxwell-Proca系统
 (7)
(7)
且利用Nehari流形方法证明了系统(7)圆柱对称基态解的存在性。
就目前现有的文献来看,众多学者都是在静电情况下(
)研究的Schrödinger-Maxwell系统,也就是我们常说的Schrödinger-Poisson系统,关于Schrödinger-Maxwell系统的静电磁解的研究未见任何研究结果。
所以受文献 [11] 、 [13] 和 [14] 的启发,本文的主要目的是研究系统(2)涡旋静电磁解的存在性,也就是形如
的解,其中
并且
如(5)中所定义,那么系统(2)退化为如下系统
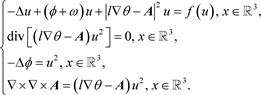 (8)
(8)
注意到,
,且选取
,则系统(8)就变成了系统(1)。
问题(1)所对应的能量泛函
定义为
. (9)
由于系统(1)中的旋度算子具有无限维的核空间,所以问题(1)的主要困难在于能量泛函I是强不定的。为了解决这个困难,我们在第二节中引入空间
,使得对于任意的
,有
.
本文主要结果陈述如下:
定理1.1 假设
并且
,那么系统(1)存在涡旋基态解
,其满足:1)
和
;
2)
。
本文结构如下。在第2节中,我们给出了一些引理并通过约化方法将(9)化为单变量泛函。在第3节中,我们利用Nehari流形方法来证明系统(1)基态解的存在性。
2. 准备工作
在本节中,我们将使用以下符号:
表示正数;
表示勒贝格空间
的范数。
2.1. 工作空间
定义Sobolev空间
,
其对应范数为
.
空间
是
的完备,其对应范数为
.
空间
是
的完备,其对应范数为
,
其中
。事实上,
,并且
在
中稠密。
2.2. 准备性引理
引理2.1 ( [2] 命题3.1)固定
,
存在唯一解
。
引理2.2 映射
是
的并且对于任意的
,有
(10)
证明:类似于文献 [15] 中命题2.1的证明,定义映射
满足
。经计算,易知
对于所有的
,
是可逆的且
。又由隐函数定理可知,对任意的
,存在唯一解
,使得
,
,
.
引理2.3 假设
,则
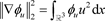 , (11)
, (11)
, (12)
并且存在
使得
. (13)
此外,
满足
, (14)
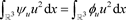 , (15)
, (15)
. (16)
证明:类似于 [12] 中引理2.1和 [16] 的引理2.2的证明,可证得引理2.3。
根据引理2.1和引理2.3,我们可考虑约化泛函
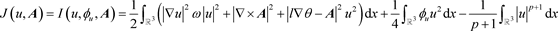 ,(17)
,(17)
其在
是
的,并且若
是J的临界点,那么
是I的临界点。
定义
,
其中
,
的范数与
的范数等价。类似地,定义空间
。
注意到,若
,则
。令
并且定义
是
的完备,其范数为
的范数,显然
。
引理2.4 ( [13] 引理15)对任意的
,有
和
。
因此,系统(1)中的最后一个方程可退化为
. (18)
定义
.
引理2.5 假设
,若对任意的
有
,则
。若对任意的
有
,则
。
证明:类似于 [11] 中定理16的证明,若对任意的
有
,我们令
.
选取任意的
,
,其中
和
,则
.
因为
和
是圆柱对称的,由稠密理论可知
,故
。
同理,假设对任意的
有
,且令
.
选取任意的
,
,其中
和
,则
.
由 [11] 中引理12知
,故
。
引理2.6 若
,那么方程(18)存在唯一解
。
证明:固定
,考虑在
上的双线性映射:
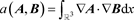 .
.
显然有
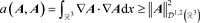 .
.
根据Hölder不等式,有
 .
.
此外,根据Sobolev嵌入定理,可得
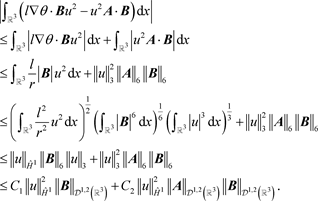
因此,线性映射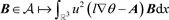 是连续的。再因Lax-Milgram定理可知,存在唯一的
,满足
是连续的。再因Lax-Milgram定理可知,存在唯一的
,满足
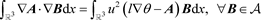 .
.
引理2.7 假设
,则
满足
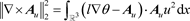 , (19)
, (19)
 , (20)
, (20)
 . (21)
. (21)
证明:若
,在系统(1)的最后一个方程左右同时乘
并在
上积分,我们很容易得到(19)。接下来,通过直接计算,可得
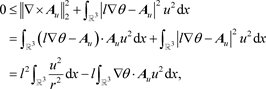
这蕴含了(20)和(21)成立。
引理2.8映射
是
的且对于任意的
,有
.
此外,
满足
, (22)
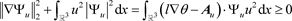 , (23)
, (23)
 . (24)
. (24)
证明:定义映射
,
满足
。经计算,有
易知对于所有的
,
是可逆的并且
。又由隐函数定理可知,对任意的
,存在唯一的
满足
,
,
.
因此,
,即
满足式(22)。
此外,由于
和(22),可得
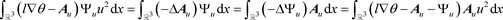 ,
,
故(24)成立。
根据引理2.2和引理2.8,我们可考虑如下的约化泛函
(25)
其在
上是
的并且若
是I的临界点当且仅当
是J的临界点,
当且仅当
是
的临界点,
和
。因此,我们只需寻找泛函
的临界点。
3. 定理1.1的证明
定义Nehari流形
.
引理3.1
是非空的。
证明:对于任意的
,固定
,定义
显然,
。对于充分小的
,有
且
。因此,根据连续函数的介值性定理可知,存在
,使得
,即
。
引理3.2 对任意的
,有
。
证明:假设
,通过计算,可得
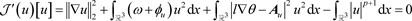 ,
,
这蕴含着
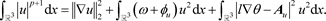 (26)
(26)
由(12)可推出 。因此,
。因此,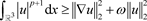 。
。
又由Sobolev嵌入定理易知,
。
引理3.3
是自然约束。
证明:假设
是
的临界点,由拉格朗日乘子定理知,存在
,使得
。
下证
。因为
,故只需证明
。
结合(16),(23)和(26),有

由于
和
,故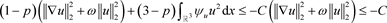 , 因此
。
, 因此
。
引理3.4 泛函
有正下界。
证明:假设
,结合(16),(21)和(26),有
故存在常数
,使得对于任意的
有
。
引理3.5 假设
是极小化序列,那么
在
上有界。
证明:假设
是极小化序列,即
.
由定理3.4可知
,
这蕴含了
在
上有界。经计算,有
(27)
故可推出
在
上有界。由基本不等式和Hölder不等式可得
(28)
结合(27)和(28),有
因此,
,故
在
上有界。
引理3.6 任意的有界序列
是非消失的。
证明:假设序列
消失,即
.
由Lions的消失引理(可见 [17] 的引理1.1)可知,当
时,
在
,这与引理3.2矛盾,证毕。
引理3.7 若
在
,那么通过选取子列,则
在
和
在
。因此,
。
证明:根据引理3.5,通过选取子列仍记为
,那么存在
,使得
在
中, (29)
在
中,其中
, (30)
在
中,其中
. (31)
由(13)可得
在
中有界,则存在
,使得
在
中, (32)
在
中, (33)
在
中,其中
. (34)
又因为
在
中有界,则存在
,使得
在
中, (35)
在
中, (36)
在
中,其中
. (37)
下证
和
。由于系统(1)后两个方程解的唯一性,故只需证明
, (38)
. (39)
记
,因为
,对
,由(31)和(32),有
因此,(38)成立。
令
和
,记
,因为
,只需证明
, (40)
, (41)
, (42)
由(35),(40)显然成立。注意到,
,并结合(30),于是(41)成立。
根据Hölder不等式,有
那么由(31),(37)及
的有界性,(42)成立。
若
且令
,则有
根据(31),(34)和
的有界性,可推出
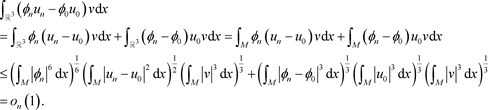
由(31),(37)和
的有界性可得
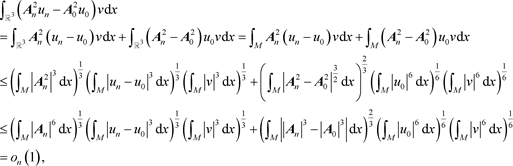
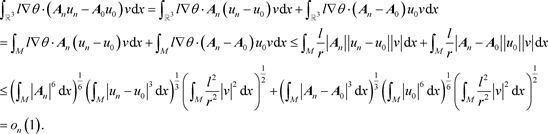
故当
时,
。
因为
是自然约束,由 [18] 中定理8.5知,可假设
是
的PS序列,即
以及对于任意的
,
。
定理1.1的证明 根据引理3.6,可知存在
,序列
,使得
.
断言:
有界。由于
具有柱对称性,则
,
其中
和
。注意到,若
,则有
,
这与
的
范数有界矛盾。故断言成立。定义
,则有
,
.
令
,那么
. (43)
根据(43)可知存在
,使得
。此外,
满足
和
.
由引理3.7可知
,故
。即u是
的临界点。结合(17)和(25)可得
.
因此,
是系统(1)的非平凡解且
。
最后我们证明u是基态解。
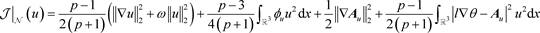 ,
,
根据Fatou引理和范数函数的弱下半连续性可知
.
4. 结论
本文研究了一类静电磁Schrödinger-Maxwell系统涡旋基态解的存在性。通过柱对称处理旋度算子,把强不定问题约化为定的问题,最后利用Nehari流形方法证明基态解的存在性。
基金项目
山西省自然科学基金面上项目( 202303021211056)。
NOTES
*通讯作者。