1. 引言
图的交叉数是图论中一个重要的部分。近百年来,国内外很多学者都对图的交叉数这一问题进行研究。图的交叉数问题的研究,起源于20世纪40年代砖厂遇到的难题。第二次世界大战时期,Turan [1] 发现运砖车沿铁轨向仓库运砖时,车很容易在铁轨交点的位置脱节。他因此想到通过减少铁轨交叉个数来降低损失的方法,交叉数的概念由此而来。研究图的交叉数是一项富有意义但充满挑战性的工作。其实,在1983年,Garey和Johnson [2] 已经证明了确定一个图的交叉数是NP-完全问题。由于证明难度较大,国内外关于图的交叉数领域的研究进展缓慢。下面主要介绍广义Petersen图的研究成果。
广义Petersen图
最早研究广义Petersen图在1981年,Exoo C,Harary和Kabel [3] 对图的交叉数进行研究,得出:
1986年Fiorini [4] 给出广义Petersen图
的交叉数的证明,但是,Richter和Salazar [5] 随后指出其证明存在错误,他们证明广义Petersen图
的交叉数为:
2004年,林晓惠 [6] 得出了
等部分广义Petersen图的交叉数的上界;2005年,马登举等人证明了
的交叉数 [7] ;2009年,杨元生等人利用算法给出了
时
的交叉数的精确值 [8] ;Fiorinil和黄元秋等人分别用不同方法证明了
的交叉数 [9] ;2013年,郑百功证明了
的交叉数 [10] 。2019年,Gauci和Xuereb [11] 证明了当
时有:
2020年,历莹 [12] 通过研究
的子图的性质,证明得出
的交叉数的下界至少是6,进而提出猜想:当
时,
。2023年,卢妮 [13] 证明了Chimani的猜想:当
时,有
。2023年,白贺 [14] 在其硕士论文中证明了双广义Petersen图的交叉数
。
2. 玫瑰花窗图
的定义
为方便书写,下文将玫瑰花窗图
记作
,其中
。设
的顶点集为
,边集为
,其中下标取模3k。
设G是一个简单图。G的一个分解是G的边不相交子图的列表,使得G的每条边都出现在列表中的一个子图中。如果对于每对整数i和j,
,G存在一个自同构
,使得
当且仅当
,则称图G的一个分解
是可传递的,其中下标取t的模。如果存在图G的一个传递分解,则称图G是广义周期图。
设
,且
为三角形
。设
为领结图
,
。设
的顶点集为
,边集为
,
。显然
是
的一个可传递分解,其中
。因此
是一个广义周期图。设
且
,
。
对于图G,设H是G的子图且
是H到所有非负实数集合的映射:
.
Jordan曲线定理 任意一条简单(自身不相交)闭曲线J把平面分成两个区域,在不同区域的两点若要相连,则连结的弧必与J相交。
根据Jordan曲线定理,我们有以下引理:
引理2.1 在图G中,设C和C'为两个顶点不相交的圈,
为k阶路径且
。假设D是G的一个好画法,则
为偶数;当
和
在
的同一区域时,
为偶数,否则为奇数。
引理2.2 设c是一个正整数,对于
,若存在一个正整数
满足
,则令
为
的最小值使
;若不存在这样的正整数
,则令
。
3. 玫瑰花窗图
的交叉数
3.1. 玫瑰花窗图
的交叉数的上界
引理3.1
。
引理3.2 对于
,
。
证明:如图1所示,给出了
的一个只有2k个交叉数的好画法。因此,当
时,
。
3.2. 玫瑰花窗图
的交叉数的下界
引理3.3 (领结引理) 设
,D是
的一个好画法且
。则
和
被
分离或
和
被
分离。
证明:假设
和
在
划分平面的同一区域。若
,由引理2.1,
,这与
矛盾。因此
。由
知
。又由于D是好的画法,所以
。因此,
和
被
分离。
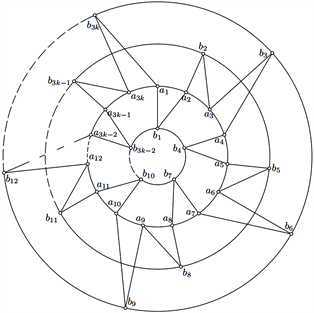
Figure 1. A good drawing of with 2k crossings
图1. 有2k个交叉点的好的画法
引理3.4 设D是
的一个好画法且
,
。若
,那么
;
,
;
,
。
证明:由
,有
,
,
。反证法。假设
,
。由引理2.1可知
,与
相矛盾。因此
,
。
假设
。由
,有
。根据引理3.3,
和
被
分离或
和
被
分离。由引理2.1,若
和
被
分离,路径
与
相交;若
和
被
分离,路径
与
相交。两种情形均有
,矛盾。因此
。
假设
。由
,有
。根据引理3.3,
和
被
分离或
和
被
分离。由引理2.1,若
和
被
分离,路径
和
与
相交;若
和
被
分离,路径
和
与
相交。两种情形均有
,矛盾。因此
。
假设
,则有
或
。假设
。由
,有
。根据
知
. 由引理2.1,
和
被
分离且路径
交
,则
,矛盾。因此
. 假设
。由
及
,有
。根据引理2.1,
和
被
分离,且由
有
和
被
分离。由引理2.1,路径
和
与
相交,与
矛盾。因此
。即
。由于
,因此
。
引理3.5 (画法引理) 设D是
的一个好画法使得
,且
,
。若路径
上有m个交叉点,则路径
上至少有
个交叉点;若路径
上有m个交叉点,则路径
上至少有
个交叉点。其中
,
。
引理3.6 设D是
的一个好画法使得
,且
,
。若
,则
同构于图3。
子情形一:
在区域
。
证明:通过
,得到
,
,
,
。由引理3.4知,
,
,
,即有
。再根据好的画法的定义,有
。当
时,
同构于图2(a)或图2(b)。
由于
,根据引理2.1,
。若
同构于图2(a),由引理2.1,路径
和
与
相交,则
,矛盾。若
同构于图2(b),由
可知,
。若
,由画法引理(引理3.5)可知,
和
都不干净。因此,
,矛盾。故
,即
。因此
同构于图2(c)。由引理2.1,路径
和
与
相交,则
,矛盾。因此,
。即
且
同构于图3。
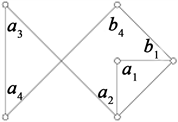
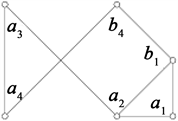
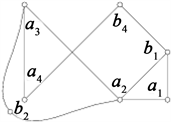 (a) (b) (c)
(a) (b) (c)
Figure 2.
and
图2.
且
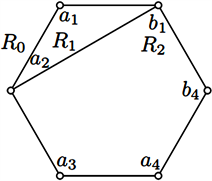
Figure 3.
and
图3.
且
引理3.7 设D是
的一个好画法且
,
。若
同构于图3,
在区域
且
,则
同构于图5。
证明:通过
,得到
,
,
,
。由引理2.1,路径
和
交圈
。若
,则由引理2.1可知
。因此,
,矛盾。故
即
。根据引理3.4,
且
。因此
同构于图4(a)。
由
可知,
。若
,根据引理3.3,
和
被
分离或
和
被
分离。若
和
被
分离,又由于
且
,则
和
位于
划分平面的不同区域。由引理2.1,路径
与
相交。由
可知,
。因此
和
位于
划分平面的不同区域。同理由引理2.1,路径
与
相交。因此,
,矛盾。若
和
被
分离,根据引理2.1,路径
与
相交。又由于
,同理由引理2.1,路径
与
相交。因此,
,矛盾。故
。若
。根据好的画法有
且
位于区域
或
。由引理2.1,路径
和
交圈
。根据
,有
。不失一般性,假设
。根据引理3.4,
且
。因此
和
位于
划分平面的同一区域。同理,由
和
可知,
和
位于
划分平面的同一区域。根据引理2.1,若
,则
。当
在区域
时,由
可知,
,因此
位于区域
或
。这两种情形,由引理2.1均有路径
与
相交。因此,
,矛盾。当
在区域
时,
同构于图4(b)。根据引理2.1可知,路径
和
交圈
。同理于上述情形,
,且
,
。因此,
,矛盾。故
。
同构于图5。
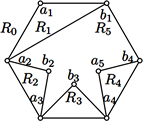
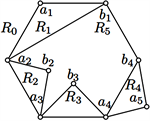
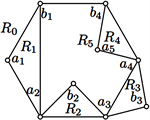
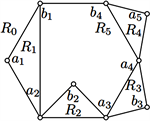 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 5.
and
are in area
图5.
且
在区域
引理3.8 设D是
的一个好画法使得
,且
,
。 若
同构于图5,则
。
情形1,
同构于图5(a);
情形2,
同构于图5(b)或图5(c);
情形3,
同构于图5(d)。
子情形二:
在区域
。
通过上述证明,当
时,总有
成立。
4. 结论
本文利用反证法和数学归纳法证明玫瑰花窗图
的交叉数。根据好的画法的定义,给出了玫瑰花窗图
的交叉数为2k的一个好画法,从而得到玫瑰花窗图
的交叉数上界;由于玫瑰花窗图
是广义周期图的一种,因此利用广义周期图的性质对图
的边集进行分类,结合计数公式,利用所得的限制条件,探究每组边上的交叉计数,最终证得玫瑰花窗图
的交叉数下界。由此得到
,
。