基于Fiducial推断的Kriging模型选择

Model Selection of Kriging Model Based on Fiducial Inference

摘要: 计算机试验异军突起，并因其经济性而越来越普遍地取代物理实验。Kriging模型作为计算机试验的元模型之一，因其使用简单、灵活被广泛地应用于各大领域。本文给出了基于Fiducial推断的Kriging模型选择方法，并与Lasso和Elastic Net惩罚下的选择方法相比较。数值模拟和实例分析表明Elastic Net惩罚下的选择方法优于Lasso，基于Fiducial推断的模型选择方法相较于Lasso和Elastic Net具有更高的拟合准确性和预测精度。

Abstract: Computer experiments are becoming increasingly popular and surrogate for physical experiments because of their economy. Kriging model, as one of the meta models of computer experiments, is widely used in various fields because of its simplicity and flexibility. This paper studies a model se-lection method based on Fiducial inference for Kriging model, and compares with the selection methods under Lasso and Elastic Net penalties. Numerical simulation and case analysis show that the selection method based on Elastic Net penalty is superior to Lasso, and the model selection method based on Fiducial inference has higher fitting accuracy and prediction accuracy compared to Lasso and Elastic Net.

1. 引言

随着科学技术的不断发展进步，计算机试验异军突起，并因其经济性而越来越普遍地取代物理实验。计算机试验的主要目标是建立一个相对简单的元模型，使其可以很好地近似原始的复杂模型，从而可以节约时间成本和试验费用。1989年Sacks等 [1] 首次提出的Kriging模型可以作为计算机试验中的元模型使用，因为它具有方便、灵活和广泛的通用性。

Kriging模型主要包括两个部分：均值函数和一个平稳的高斯过程。当均值函数是一个常数时，称为ordinary Kriging (OK)模型，若在均值函数中假设一些预先指定的变量，则称为Universal Kriging (UK)模型，也称为一般Kriging模型，目前在研究领域被广泛使用。计算机试验通常会包含大量的输入变量，因此，能够准确地识别出哪些变量对输出结果是有重要作用的变量是非常关键的。Welch等 [2] 在1992年提出了计算机试验变量选择的概念。他们在均值函数是常数的情形下，选择出对高斯过程影响比较大的一些变量。在Welch等人思想的鼓舞下，Li和Sudjianto [3] 提出了惩罚似然的方法，Linkletter等 [4] 使用贝叶斯方法选择出对高斯过程影响较大的变量。

目前的Kriging模型的变量选择问题从对高斯过程的讨论转移到了均值函数上，均值函数不再是单一的常数值，而是包含了一些预先指定变量的函数，此时我们关注的重点放在了如何从均值函数中准确地选择出主要变量。之所以会发生这样的转变，是因为OK模型的恒定均值不足以捕捉总体趋势，采用UK模型对于建立较为精确的Kriging模型是合理的。Zhang [5] 提出了一种均值函数的新的惩罚方法，并从贝叶斯观点出发证明了该方法的有效性。Hung [6] 采用惩罚似然方法对均值函数进行变量选择，李涵等 [11] 在Lasso和Adaptive Lasso惩罚似然的基础上，提出Elastic Net惩罚，并证明了基于Elastic Net惩罚的选择方法在拟合和预测上都优于其他两种。然而基于贝叶斯思想的选择方法在很大程度上依赖于先验的选择，不合适的先验可能会导致一个较差的结果；基于惩罚似然的选择方法往往会导致过拟合现象，更倾向于选择一个较大模型作为最优模型。

近些年，Fiducial推断理论重新兴起，基于Fiducial推断的模型选择方法开始迅速发展。不同于贝叶斯方法，Fiducial推断不依赖于先验信息，避免了先验信息选取不当带来的影响，它还可以给出每个候选模型是最优模型的概率保证。赵勇超等 [12] 基于Fiducial推断研究了高维线性模型的变量选择问题，结果表明所提出方法具有一定的优越性。本文主要基于Fiducial推断对Kriging模型均值函数进行变量选择，并与李涵等 [11] 提出的基于Lasso和Elastic Net惩罚的选择方法比较拟合和预测效果。文章主要结构如下：第二部分介绍Kriging模型的基础理论知识；第三部分介绍基于Fiducial推断的模型选择方法；第四部分通过数据模拟给出变量选择的结果和预测效果；第五部分进行实例分析；最后给出结论。

2. 一般Kriging模型

假设 $x_i,i=1,\cdots ,n$ 是d维试验区域上的设计点， $y_i=y\left(x_i\right)$ 是 $x_i$ 对应的输出值，则一般Kriging模型定义为：

$y_i={\beta }_0+{\displaystyle \underset{j-1}{\overset{p-1}{\sum }}{f}_j\left(x_i\right){\beta }_j}+z\left(x_i\right),i=1,\cdots ,n$ , (1)

其中 $\left\{1,f_1\left(x\right),\cdots ,f_{p-1}\left(x\right)\right\}$ 是基向量， $f_j\left(x\right),j=1,\cdots ,p-1$ 是基函数， ${\beta }_j$ 是回归系数， $z\left(x\right)$ 是一个高斯随机过程，其均值为0，协方差函数为

$\mathrm{cov}\left(z\left(x_i\right),z\left(x_j\right)\right)={\sigma }^{2}r\left(x_i,x_j;\varphi \right)$ ,

$r\left(x_i,x_j;\varphi \right)$ 是 $z\left(x\right)$ 的相关函数，与空间相关参数 $\varphi$ 有关。协方差函数种类多样，这里我们只考虑平方指数协方差函数，即

$\mathrm{cov}\left(z\left(x_i\right),z\left(x_j\right)\right)={\sigma }^2\exp \left(-{\displaystyle \underset{k=1}{\overset{d}{\sum }}\frac{{\left|x_{ik}-x_{jk}\right|}^2}{{\phi }_k^2}}\right)$ .

为了方便表示，我们给出上述Kriging模型的矩阵记号

$y=F\beta +\sigma R^{\frac{1}{2}}U,U~N\left(0,I_n\right)$ ,(2)

其中 $y={\left(y_1,\cdots ,y_n\right)}^{\prime }$ ， $\beta ={\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_{p-1}\right)}^{\prime }$ ， $\varphi ={\left({\phi }_1,{\phi }_2,\cdots ,{\phi }_d\right)}^{\prime }$ ， $\theta =\left(\beta ,{\sigma }^2,\varphi \right)$ 是 $p+d+1$ 维参数向量。 $R\left(\varphi \right)$ 是基于平方指数协方差函数得到的相关系数阵，它的 $\left(i,j\right)$ 位置的元素为 $r\left(x_i,x_j;\varphi \right)$ ，设计矩阵F具有以下形式

$\left(\begin{array}{cccc}1& f_1\left(x_1\right)& \cdots & f_{p-1}\left(x_1\right)\\ 1& f_1\left(x_2\right)& \cdots & f_{p-1}\left(x_2\right)\\ ⋮& ⋮& \ddots & ⋮\\ 1& f_1\left(x_n\right)& \cdots & f_{p-1}\left(x_n\right)\end{array}\right)$ .

Santner等 [7] 表明最大似然估计优于交叉验证估计，所以本文使用最大似然估计来估计参数，Kriging模型的对数似然函数为：

$l\left(\theta |y\right)=-\frac{n}{2}\log \left(2\pi \right)-\frac{1}{2}\log \left({\sigma }^2\right)-\frac{1}{2}\log \left|R\left(\varphi \right)\right|-\frac{1}{2{\sigma }^2}{\left(y-F\beta \right)}^{\prime }{R}^{-1}\left(\varphi \right)\left(y-F\beta \right)$ ,(3)

当参数 $\varphi$ 已知时，可得到 $\left(\beta ,{\sigma }^2\right)$ 的极大似然估计为：

$\hat{\beta }={\left(F^{\prime }{R}^{-1}\left(\varphi \right)F\right)}^{-1}{F}^{\prime }{R}^{-1}\left(\varphi \right)y$ , (4)

${\hat{\sigma }}^2=\frac{{\left(y-F\hat{\beta }\right)}^{\prime }{R}^{-1}\left(\varphi \right)\left(y-F\hat{\beta }\right)}{n}$ , (5)

参数 $\varphi$ 未知时，由于似然函数对 $\varphi$ 的偏导很难计算，其极大似然估计没有解析形式。因此只能通过数值计算的方法给出其近似解：

$\hat{\varphi }=\underset{\varphi }{\text{argmin}}\left\{\log \left|R\left(\varphi \right)\right|+n\log \left({\hat{\sigma }}^2\right)\right\}$ . (6)

当求得参数 $\theta$ 的估计值 $\hat{\theta }=\left(\hat{\beta },{\hat{\sigma }}^2,\hat{\varphi }\right)$ 后，对于新的数据点 $x^{*}$ ，其对应的预测值为：

$\hat{y}\left(x^{*}\right)=f{\left(x^{*}\right)}^{\prime }\hat{\beta }+r\left(x^{*},X\right)R^{-1}\left(\hat{\varphi }\right)\left(y-F\hat{\beta }\right)$ ,(7)

其中 $f\left(x^{*}\right)={\left(1,f_1\left(x^{*}\right),\cdots ,f_{p-1}\left(x^{*}\right)\right)}^{\prime }$ ， $r\left(x^{*},X\right)$ 是一个 $1\times n$ 的行向量，表示 $z\left(x^{*}\right)$ 与 $z\left(X\right)$ 之间的相关性。

3. Fiducial模型选择方法

3.1. 广义Fiducial推断

Fiducial推断的思想最早起源于Fisher [8] ，但在当时并没有引起大家的重视，直到21世纪初，一些学者重新开始研究Fiducial，并且对其进行了各种变形使用，用于解决各种推断问题。目前使用最广泛的当属广义Fiducial推断(GFI)，不需要参数的先验信息也可以对参数估计进行统计推断。

假定描述数据y和参数 $\theta$ 关系的表达式为：

$y=G\left(U,\theta \right)$ , (8)

其中 $G\left(\cdot ,\cdot \right)$ 是一个确定的函数，称为数据生成方程，U是分布已知的随机向量，并且与参数 $\theta$ 是独立的。给定y的情况下，如果对于任意的 $\theta$ ， $G^{-1}$ 均存在，则

.

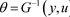已知U的分布，多次重复抽样U，通过结构方程的逆可以得到一组关于 $\theta$ 的随机样本，我们称之为 $\theta$ 的Fiducial样本，与之相对应的密度称为 $\theta$ 的Fiducial密度，记为 $r\left(\theta |y\right)$ 。

Hannig等人 [9] 在2016年提出了Fiducial密度的一种易于计算的版本，在对似然函数施加一定的光滑性假设下，参数 $\theta$ 的Fiducial密度可以写成：

$r\left(\theta |y\right)=\frac{f\left(y,\theta \right)J\left(y,\theta \right)}{{\displaystyle {\int }_{\Theta }f\left(y,\theta \right)J\left(y,\theta \right)\text{d}\theta }}$ , (9)

其中：

$J\left(y,\theta \right)=D\left({\frac{\text{d}}{\text{d}\theta }G\left(u,\theta \right)|}_{u=G^{-1}\left(y,\theta \right)}\right)$ , (10)

且 $D\left(A\right)={\left(\det A^{\prime }A\right)}^{\frac{1}{2}}$ ， $G^{-1}\left(y,\theta \right)$ 是结构方程关于u的逆。

3.2. Fiducial模型选择方法

对于一般Kriging模型，假设候选模型集为 $\mathcal{M}=\left\{M_1,M_2,\cdots ,M_K\right\}$ ，则模型M可以表示为：

$y=G\left(M,{\theta }_M,U\right)=F_M{\beta }_M+{\sigma }_M{R}^{\frac{1}{2}}\left({\varphi }_M\right)U$ , (11)

其中 $M\in \mathcal{M}$ 是候选模型之一， ${\theta }_M\in {\Theta }_M$ 是模型M中包含的未知参数， ${\beta }_M\in R^p$ ， ${\sigma }_M,{\varphi }_M>0$ ，U是与参数独立且分布已知的随机向量。

为了计算方便，我们对其作了简单的转换：

$\tilde{y}=\tilde{G}\left(M,{\theta }_M,U\right)={\tilde{F}}_M{\beta }_M+{\sigma }_{M}U$ ,

其中 $\tilde{y}=R^{-\frac{1}{2}}\left({\varphi }_M\right)y$ ， ${\tilde{F}}_M=R^{-\frac{1}{2}}\left({\varphi }_M\right)F_M$ ，根据公式(10)可以计算出：

$J\left(\tilde{y},{\theta }_M\right)={\sigma }_M^{-1}{\left|{{\tilde{F}}^{\prime }}_M{\tilde{F}}_M\right|}^{\frac{1}{2}}RS{S}_M^{\frac{1}{2}}$ ,

其中 $RS{S}_M={\left(\tilde{y}-{\tilde{F}}_M{\hat{\beta }}_M\right)}^{\prime }\left(\tilde{y}-{\tilde{F}}_M{\hat{\beta }}_M\right)$ ， ${\hat{\beta }}_M={\left({{\tilde{F}}^{\prime }}_M{\tilde{F}}_M\right)}^{-1}{{\tilde{F}}^{\prime }}_M\tilde{y}$ 。

广义Fiducial推断倾向于变量选择较多的模型，为了防止过拟合，Hannig和Lee [10] 在GFI的框架下引入了惩罚，即对每个候选模型加上一个惩罚约束

$0=P_k,k=1,\cdots ,\min \left(\left|M\right|,n\right)$ ,

其中 $\left|M\right|$ 是模型M中变量的个数， $P_k$ 是独立同分布的连续随机变量，且满足 $f_P\left(0\right)=q$ ，其中q是一个确定的惩罚常数。基于最小描述长度的思想，使用 $q=n^{-1/2}$ 作为默认惩罚值，并给出了候选模型M的Fiducial概率：

$r\left(M|y\right)=\frac{q^{\left|M\right|}{\displaystyle {\int }_{{\Theta }_M}{f}_M\left(y,{\theta }_M\right)J_M\left(y,{\theta }_M\right)\text{d}{\theta }_M}}{{\displaystyle {\sum }_{M^{\prime }\in \mathcal{M}}{q}^{\left|M^{\prime }\right|}{\displaystyle {\int }_{{\Theta }_{M^{\prime }}}{f}_{M^{\prime }}\left(y,{\theta }_{M^{\prime }}\right)J_{M^{\prime }}\left(y,{\theta }_{M^{\prime }}\right)\text{d}{\theta }_{M^{\prime }}}}}$ .

当参数 $\varphi$ 已知时，对于任意候选模型 $M\in \mathcal{M}$ ，我们可以给出模型M的Fiducial概率：

$r\left(M|\tilde{y}\right)\propto R\left(M\right)=n^{-\frac{\left|M\right|}{2}}\Gamma \left(\frac{n-\left|M\right|}{2}\right){\left(\pi RS{S}_M\right)}^{-\frac{n-\left|M\right|-1}{2}}$ . (12)

当参数 $\varphi$ 未知时，根据(4)~(6)式，可以给出候选模型M下的参数估计 $\left({\hat{\beta }}_M,{\hat{\sigma }}_M^2,{\hat{\varphi }}_M\right)$ ，再按照参数 $\varphi$ 已知时的情况代入公式(12)，可求得模型M的Fiducial概率 $\hat{r}\left(M\right)$ 。然后找出候选模型集 $\mathcal{M}$ 中模型Fiducial概率最大的作为最优模型，即

$\hat{M}=\underset{M\in \mathcal{M}}{\arg \max }\hat{r}\left(M\right)$ . (13)

算法1给出了一般Kriging模型下Fiducial推断变量选择的具体实现步骤。

Algorithm 1. Variables selection method of Fiducial inference under the universal Kriging model

算法1. 一般Kriging模型下Fiducial推断变量选择方法

4. 数值模拟

李涵等 [11] 提出了Elastic Net惩罚下的变量选择方法，并验证了基于Elastic Net惩罚的选择方法在拟合和预测上都优于其他方法。本节对提出的Fiducial模型选择方法(FUK)进行数值模拟，并将其模拟结果与Lasso惩罚(LUK)、Elastic Net惩罚(ENUK) [11] 的方法进行比较。比较的指标主要包括两方面：一方面是变量识别的准确性，主要有积极变量识别率的平均(AEIR)；消极变量识别率的平均(IEIR)；积极变量个数的平均(MEAN)。另一方面是预测精度，主要有均方根预测误差的平均值(MRMSPE)和标准差(sd(RMSPE))。AEIR越大，说明所选模型中包含的积极变量越多，故AEIR越大越好；IEIR，RMAPE，sd(RMSPE)越小越好，MEAN越接近真模型越好。

4.1. 模拟1：线性函数

已知函数模型：

, (14)

输入维数 $d=12$ ，X均匀分布在 ${\left[0,1\right]}^{12}$ ， $x_1,\cdots ,x_6$ 的系数越来越小， $x_7,\cdots ,x_{12}$ 的系数均为零。 $\epsilon \left(x\right)~N\left(0,{\sigma }^{2}R\right)$ ， $\sigma =0.05$ ，R是相关系数矩阵，参数 ${\varphi }_k=1,k=1,\cdots ,d$ 。本模拟通过拉丁超立方抽样产生 $d=12$ ，样本量分别为 $N=50,80,100$ 的样本D。测试集T由随机生成的1000个样本点组成。基于500次重复实验，模拟结果在表1中给出。

通过表1的结果可以得到，从积极变量识别率AEIR来看，LUK和ENUK差别不大，N = 50时，FUK不如LUK、ENUK高，但随着样本量的增加，FUK的AEIR开始高于LUK、ENUK。无论样本量大小，FUK的消极变量识别率IEIR一直为0，说明Fiducial选择的最优模型中没有包含消极变量，而LUK、ENUK一直都包含消极变量，随着样本量的增加IEIR逐渐减小，ENUK的IEIR要略小于LUK。从根均方预测误差RMSPE来看，ENUK的预测误差要小于LUK，且误差标准差也小于LUK，FUK的预测误差小于LUK、ENUK，具有良好的预测效果。综上来看，FUK在积极变量识别率只有在样本量较大时能够展现出优势，但在消极变量识别率上有优势，而且在预测方面也优于LUK和ENUK，这说明Fiducial模型选择方法的准确性和稳定性更优。

Table 1. Data simulation results of linear function model (14)

表1. 线性函数模型(14)的数值模拟结果

4.2. 模拟2：非线性钻孔函数

钻孔函数 [13] 模型：

$y\left(x\right)=2\pi x_3\left(x_4-x_6\right){\left\{\log \left(\frac{x_2}{x_1}\right)\left(1+2\frac{x_3{x}_7}{\log \left(x_2/x_1\right)x_1^2{x}_8}+\frac{x_3}{x_5}\right)\right\}}^{-1}$ , (15)

输入维数 $d=8$ ，输入空间为[0.05, 0.15] × [100, 5000] × [63070, 115600] × [990, 1110] × [63.1, 116] × [700, 820] × [1120, 1680] × [9855, 12045]，拟合模型使用一般Kriging模型 $y\left(x\right)=m\left(x\right)+z\left(x\right)$ ，设定均值函数形式为 $m\left(x\right)={\beta }_0+{\beta }_1{x}_1+\cdots +{\beta }_8{x}_8$ 。通过拉丁超立方抽样生成 $d=8$ ，样本量 $N=100$ 的样本D，测试集T由计算机随机生成的1000个样本点组成。基于500次重复试验，模拟结果在表2给出。

Table 2. Data simulation results of nonlinear borehole function model (15)

表2. 非线性钻孔函数模型(15)的数值模拟结果

从表2可以看出，FUK的AEIR高于LUK、ENUK，最优模型中包含积极变量的个数是最多的，且积极变量的个数也最接近真实模型。从预测效果看，FUK的平均根均方预测误差MRMSPE最小，预测效果最好。可见FUK不仅在线性模型中选择变量和预测效果好，在拟合非线性模型上，也具有很好的优良性质。

5. 实例分析

活塞拍击的声音是一种由活塞二次运动引起的发动机噪音。为了降低活塞拍击的噪音，选取了6种对噪音影响较大的因素进行分析，希望通过改变这6种因素达到减少噪音的目的。6种因素分别为活塞和气缸套之间的设定间隙x₁，峰值压力位置x₂，裙部长度x₃，裙部轮廓形状x₄，裙部椭圆度x₅，活塞销偏置x₆。数据集来源于Huang等 [14] ，共包含100个观测样本，每个样本有6个输入变量，模型中可能包含所有的线性主效应、二次主效应以及正交多项式编码下的所有双因素相互作用，因此共有72个基变量。我们从100个样本中取80个作为训练集，剩下的20个做测试集，模拟结果在表3中给出。

Table 3. Data simulation results of a piston slap noise example

表3. 活塞拍击噪声实例的数据模拟结果

从表3可以得出，从平均模型长度看，FUK比LUK要长一点，但和ENUK相差不大。从平均根均方预测误差MRMSPE来看，FUK比LUK、ENUK小，预测效果更好，且结果比较稳定。总体来看，FUK 方法能够在有效简化模型同时具有较好的预测效果。

6. 结论

本文给出了一般Kriging模型的Fiducial模型选择方法FUK，并将其与Lasso和Elastic Net惩罚下的模型选择方法(LUK、ENUK)相比较，通过两个模拟和一个实例我们得到：三种方法中最好的是FUK，其次是ENUK，最后是LUK。ENUK在拟合和预测方面均优于LUK好，FUK不但在消极变量识别率上有着显著的优势，而且预测误差小于LUK、ENUK，这说明FUK预测效果好且比较稳定。