自适应模糊ARDL时间序列半参数模型

An Adaptive Fuzzy Autoregressive Distributed Lag Time Series Based on Semi-Parametric Model

摘要: 传统的模糊最小二乘时间序列模型在包含异常值的模糊数据集中表现出较差的性能。通过引入异常值检测策略，提出了一种降低异常值对未来预测影响的方法。为此，本文介绍了一种基于半参数技术的自适应模糊自回归分布滞后(ARDL)时间序列模型，该模型将半参数技术与加权最小二乘结合，根据加权平方距离误差，提出了在存在异常值时确定精确系数的估计程序，然后利用迭代算法对模糊时间序列模型的参数进行了估计。本文还扩展了传统时间序列模型中常用的几种拟合优度准则，以比较所提出的模糊时间序列方法与现有方法的性能。通过实际例子，验证了本文方法的有效性。结果清楚地表明，在模糊数据存在潜在异常值的情况下，本文提出的模型对模糊时间序列数据的预测具有可行性和有效性，优于其他模糊时间序列模型。

Abstract: The traditional fuzzy least squares time series model shows poor performance in fuzzy data sets containing outliers. By introducing the outlier detection strategy, a method is proposed to reduce the influence of outlier on future prediction. For this purpose, this paper introduces an adaptive fuzzy autoregressive distributed lagdistributed (ARDL) time series model based on semi-parametric techniques. The model combines the semi-parametric techniques with the weighted least squares and proposes an estimation procedure to determine the exact coefficient when there are outliers according to the weighted square distance error. Then, the parameters of the fuzzy time series model are estimated by an iterative algorithm. Several goodness-of-fit criteria commonly used in traditional time series models are extended to compare the performance of the proposed fuzzy time series method with existing methods. A practical example is given to verify the effectiveness of this method. The results clearly show that the proposed model has reliability and effectiveness for the prediction of fuzzy time series data when there are potential outliers in fuzzy data, which is better than other fuzzy prediction models.

1. 引言

时间序列预测方法在商业、金融、计算机科学、工程、医学、物理、化学等许多跨学科领域都有广泛的应用。经典的统计时间序列方法侧重于各种精确的数据集。然而，在现实世界中，许多概念不能用精确的值来表示。对于这种情况，模糊时间序列模型在过去几十年中由于其在统计学和工程学中的广泛应用而获得了相当大的关注，例如招生 [1] ，股票指数价格 [2] ，温度 [3] ，财务预测 [4] 和农产品 [5] 等。

Song and Chissom [6] 首先提出了模糊时间序列的概念，并针对精确数据给出了模糊时间序列模型求解方法。模糊时间序列预测模型主要分为三个步骤。首先第一步划分论域，通过在模糊分区中将“话语范围”从精确时间序列中划分出来，对精确数据进行模糊化，其次，第二步通过识别模糊逻辑关系对预测值进行转换。最后，使用去模糊化方法将模糊量转换为精确值 [7] 。第二步对所提模型的预测性能起着重要作用。此后，第二步中的模糊逻辑关系识别技术引起了许多研究者的兴趣，并得到了广泛的研究。模糊逻辑关系识别技术主要包括模糊逻辑关系群和模糊逻辑关系矩阵 [8] 、软计算技术 [9] 以及采用模糊逻辑的统计技术等 [10] 。

对于非模糊时间序列数据，这些方法首先提供一些模糊时间序列预测值，然后将其去模糊化为精确预测值作为最终目标。其他方法依赖于模糊时间序列数据和模糊预测。在这些方法中，假设可用的时间序列数据可以用模糊数据而不是精确值来报告，其目标是用模糊量来预测未来。在这方面，Tseng和Tzeng [11] 提出了模糊季节性ARIMA模型，该模型提出了未来预测的模糊置信区间。Hesamian和Akbari [12] 提出了一种基于模糊数据的统计时间序列模型。他们提出了一个具有模糊数据、非模糊系数和模糊平滑函数的半参数时间序列模型。Zarei et al. [13] 对Hesamian和Akbari [12] 模型进行了拓展，对模糊数据采用了不同的距离度量。Hesamia et al. [14] 提出了基于模糊数据的模糊非参数时间序列模型，将非参数和核平滑方法进行了有效结合。受非参数回归模型和核平滑方法的启发，Hesamian et al. [15] 将非参数回归模型和核平滑方法结合，提出了一种基于三阶段非参数核函数法的估计程序，用于未知非线性模糊平滑函数的中心以及左右展形。

值得注意的是，在Hesamian和Akbari [12] 的方法中，提出了一种带有模糊数据的半参数时间序列模型。该方法依赖于线性回归分析中常用的最小二乘误差技术。然而，在存在异常值的情况下，最小二乘法可能提供较差的预测。在这种情况下，与最小二乘技术相比，稳健方法可以提供更高程度的准确性，因为它们使用加权机制来加权异常值。为此，本文提出了一个简单的加权最小二乘目标，以减少异常值对预测的影响，而且将数据的变化序列分成三个分量，同时还考虑了不确定性大小和模糊程度之间可能存在的关系。然后用一些常见的拟合优度准则来检验改进方法的性能，并且通过一个实际例子来验证了所提模型的效果，数值结果清楚地表明，与其他方法相比，该方法提供了足够精确的结果，特别是在数据集中存在异常值时。

本文的其余部分组织如下：第2节回顾了模糊数和模糊时间序列、模糊自回归分布滞后模型、模糊半参数时间序列模型的一些必要概念。在第3节中，提出了一种基于半参数技术的自适应模糊自回归分布滞后(ARDL)时间序列模型。第4节利用一个实际生活中的例子进行了一些比较研究，同时以一些常见的性能度量来评估所提出方法的性能。最后，第5节将对本文的主要贡献进行总结。

2. 预备知识

本节将介绍模糊数和模糊时间序列、模糊自回归分布滞后模型和模糊半参数时间序列模型的基本概念。

2.1. 模糊数和模糊时间序列

给定论域 $ℝ$ ，模糊集 $\tilde{A}$ 由其隶属函数 ${\mu }_{\tilde{A}}\left(x\right):ℝ\to \left[0,1\right]$ 定义，对于 $\alpha \in \left[0,1\right]$ ， $\left\{x\in ℝ|\tilde{A}\left(x\right)\ge \alpha \right\}$ 称为模糊集 $\tilde{A}$ 的 $\alpha$ –水平集，并记作 $\text{A}\left[\alpha \right]$ ，如果对于 $\forall \alpha \in \left[0,1\right]$ ， $\text{A}\left[\alpha \right]$ 是有限闭区间，则实数域 $ℝ$ 上的模糊集 $\tilde{A}$ 称为 $ℝ$ 上的一个模糊数。LR–型模糊数是比较常用的模糊变量，一个LR–型模糊数 $\tilde{A}$ 由其隶属函数定义得到 [16] ：

${\mu }_{\tilde{A}}\left(x\right)=\{\begin{array}{ll}L\left(\frac{a-x}{l_a}\right),\hfill & x\le a,\hfill \\ R\left(\frac{x-a}{u_a}\right),\hfill & x>a.\hfill \end{array}$ (1)

其中，中心值 $a\in ℝ$ ，左展形 $l_a>0$ 和右展形 $u_a>0$ ， $L,R:{ℝ}^{+}\to \left[0,1\right]$ ， $L,R$ 是严格递减的形状函数，且满足 $L\left(0\right)=R\left(0\right)=1$ 。一个LR–型模糊数可以记为 $\tilde{A}={\left(a;l_a,u_a\right)}_{LR}$ 。当 $l_a=u_a=0$ 时，LR型模糊数退化为清晰值a。

当 $L=R$ 且 $l_a=u_a=s$ 时，LR–型模糊数为对称模糊数，记为 $\tilde{A}={\left(a;s\right)}_L$ 。当形状函数 $L\left(x\right)=R\left(x\right)=\max \left\{0,1-x\right\}$ 时，LR–型模糊数为三角模糊数，记作 $\tilde{A}={\left(a;l_a,u_a\right)}_T$ ，若 $l_a=u_a=s$ ，LR–型模糊数为对称三角模糊数，记作 $\tilde{A}={\left(a;s\right)}_T$ 。

设 $ℝ$ 的子集 $X\left(t\right)\left(t=\cdots ,0,1,2,\cdots \right)$ 是定义在模糊集 $f_j\left(t\right)\left(j=1,2,\cdots \right)$ 的论域， $F\left(t\right)$ 是 $f_j\left(t\right)\left(j=1,2,\cdots \right)$ 的集合，则 $F\left(t\right)$ 称为 $X\left(t\right)\left(t=\cdots ,0,1,2,\cdots \right)$ 上的模糊时间序列 [1] 。

根据Coppi et al. [17] ，本文给出了基于LR–型模糊数之间偏差平方的距离的定义，假设 $\tilde{A}={\left(a;l_a,u_a\right)}_{LR}$ 和 $\tilde{B}={\left(b;l_b,u_b\right)}_{LR}$ ，则 $\tilde{A}$ 与 $\tilde{B}$ 之间偏差平方距离定义如下：

$d^2\left(\tilde{A},\tilde{B}\right)={\left(a-b\right)}^2+{\left\{\left(a-L{l}_a\right)-\left(b-L{l}_b\right)\right\}}^2+{\left\{\left(a+R{u}_a\right)-\left(b+R{u}_b\right)\right\}}^2,$ (2)

其中， $L={\displaystyle {\int }_0^1{L}^{-1}\left(w\right)\text{d}w},R={\displaystyle {\int }_0^1{R}^{-1}\left(w\right)\text{d}w}$ 。

当 $\tilde{A}$ 和 $\tilde{B}$ 是对称模糊数时，即 $\tilde{A}={\left(a;s_a\right)}_L$ 和 $\tilde{A}={\left(b;s_b\right)}_L$ 距离定义为：

$d^2\left(\tilde{A},\tilde{B}\right)=3{\left(a-b\right)}^2+2L^2{\left(s_a-s_b\right)}^2,$ (3)

特别地，当 $\tilde{A}$ 和 $\tilde{B}$ 是对称三角模糊数时，距离定义为：

$d^2\left(\tilde{A},\tilde{B}\right)=3{\left(a-b\right)}^2+\frac{1}{2}{\left(s_a-s_b\right)}^2.$ (4)

2.2. 模糊自回归分布滞后模型

考虑 ${\tilde{Y}}_t\left(t=1,2,\cdots \right)$ 是模糊时间序列，是响应变量， $X_k\left(k=1,2,\cdots \right)$ 是解释变量，Eren [18] 提出了模糊自回归分布滞后模型，该模型是一种包含因变量和解释变量以模糊线性函数形式的滞后的标准最小二乘回归模型，模糊自回归分布滞后模型(ARDL)具体如下 [18] ：

${\tilde{Y}}_t={\tilde{A}}_0+{\tilde{A}}_{1}t+{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\tilde{\theta }}_i{Y}_{t-i}}+{\displaystyle \underset{j=1}{\overset{k}{\sum }}{\displaystyle \underset{I_j=0}{\overset{q_j}{\sum }}}}{\tilde{\beta }}_{j,I_j}{X}_{j,t-I_j}+{\tilde{\epsilon }}_t=\tilde{A}{Y}_t^{*}+{\tilde{\epsilon }}_t.$ (5)

其中， $Y_t^{*}={\left[1t{Y}_{t-i}{X}_{j,t-I_j}\right]}^{\prime }$ 是自变量向量， $\tilde{A}={\left[{\tilde{A}}_0{\tilde{A}}_1{\tilde{\theta }}_i{\tilde{\beta }}_{j,I_j}\right]}^{\prime }$ 是模糊系数向量，表示为对称三角模糊数，记作 $\tilde{A}={\left(\alpha ,c\right)}_T$ ，其中 $\alpha$ 为中心值，c为展形， ${\tilde{\epsilon }}_t$ 是随机模糊误差项。Eren [18] 通过线性规划问题来确定模糊线性回归中的未知参数，具体如下：

$\begin{array}{l}\underset{\alpha ,c}{\min }{c}^{\prime }{Y}_t^{*}\\ \text{s}\text{.t}\{\begin{array}{l}{Y}_t\le \left|L^{-1}\left(h\right)\right|c{Y}_t^{*}+\alpha Y_t^{*},\hfill \\ -Y_t\le \left|L^{-1}\left(h\right)\right|c{Y}_t^{*}-\alpha Y_t^{*},\hfill \\ c\ge 0,t=1,\cdots ,T.\hfill \end{array}\end{array}$ (6)

在上述表达式中， $L\left(x\right)=\max \left\{0,1-x\right\},x\in {ℝ}^{+}$ ，h是控制展形宽度的阈值，且 $0\le h\le 1$ 。

2.3. 模糊半参数时间序列模型

我们考虑 ${\tilde{Y}}_t\left(t=1,2,\cdots \right)$ 是模糊时间序列，可以建立模糊半参数时间序列模型：

${\tilde{Y}}_t={\displaystyle \underset{i=1}{\overset{p}{\sum }}{\theta }_i}{\tilde{Y}}_{t-i}+\tilde{f}\left({\tau }_t\right)+{\tilde{\epsilon }}_t,t=p+1,p+2,\cdots ,T.$ (7)

其中， ${\theta }_i\left(i=1,2,\cdots ,p\right)$ 是待估计的未知实值系数， $\tilde{f}\left({\tau }_t\right)={\left(f\left({\tau }_t\right);l_{f\left({\tau }_t\right)},r_{f\left({\tau }_t\right)}\right)}_{LR}$ 是未知的模糊光滑函数，且 $l_{f\left({\tau }_t\right)},r_{f\left({\tau }_t\right)}\ge 0$ ， ${\tau }_t=\frac{t}{T}$ 是协变量， ${\tilde{\epsilon }}_t={\left({\epsilon }_t;l_{{\epsilon }_t},r_{{\epsilon }_t}\right)}_{LR}$ 是随机模糊误差。为了估计系数和模糊光滑函数， Hesamian and Akbari [12] 提出了一种基于核拟合方法和平方误差距离的两步法。第一步首先选择核函数，其次利用交叉验证法求解最优带宽，第二步利用平方误差距离求解未知系数。

3. 建立模型

在本节中，我们考虑了一种基于半参技术的自适应模糊ARDL时间序列模型，并考虑了加权最小二乘法去估计未知参数，给出了一些经典评价指标去评估模型效果。

3.1. 基于半参数技术的自适应模糊ARDL时间序列模型

假设我们有一组模糊时间序列数据 ${\tilde{r}}_t\left(t=1,2,\cdots ,T\right)$ ，其中 ${\tilde{r}}_t={\left(c_t;l_t,u_t\right)}_{LR}$ 。在实际应用中，与参数和非参数统计推断相比，半参数统计推断通常会产生更稳健和灵活的结果。为此，我们考虑以下基于半参数技术的自适应模糊ARDL时间序列模型：

$\{\begin{array}{l}{c}_t={\alpha }_1{c}_{t-1}+{\alpha }_2{c}_{t-2}+\cdots +{\alpha }_p{c}_{t-p}+f\left({\tau }_t\right)+{\epsilon }_{c,t},\hfill \\ l_t={\beta }_0+{\beta }_1{l}_{t-1}+{\beta }_2{l}_{t-2}+\cdots +{\beta }_q{l}_{t-q}+{\gamma }_1{\hat{c}}_t+{\epsilon }_{l,t},\hfill \\ u_t={\phi }_0+{\phi }_1{u}_{t-1}+{\phi }_2{u}_{t-2}+\cdots +{\phi }_m{u}_{t-m}+{\gamma }_2{\hat{c}}_t+{\epsilon }_{u,t},t=k+1,\cdots ,T\hfill \end{array}$ (8)

其中， $k=\max \left(p,q,m\right)$ ， ${\alpha }_1,\cdots ,{\alpha }_p,{\beta }_0,{\beta }_1,\cdots ,{\beta }_q,{\gamma }_1,{\phi }_0,{\phi }_1,\cdots ,{\phi }_m,{\gamma }_2$ 为需要估计的未知实值系数， ${\epsilon }_{c,t},{\epsilon }_{l,t},{\epsilon }_{u,t}$ 分别是中心，左展形，右展形的误差项， ${\hat{c}}_t$ 是 $c_t$ 的估计值， $f\left({\tau }_t\right)$ 是未知的光滑函数， ${\tau }_t=\frac{t}{T}$ 是协变量。

为了准确估计系数和光滑函数，我们引入了一个两阶段的方法，首先根据Wang et al. [19] ，未知光滑函数的估计值 $\hat{f}\left({\tau }_t\right)$ 为：

$\hat{f}\left({\tau }_t\right)={\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)\left(c_j-{\displaystyle \underset{l=1}{\overset{p}{\sum }}{\alpha }_l}{c}_{j-p}\right),$ (9)

其中， $w_j\left({\tau }_t\right)=\frac{\frac{1}{Th}K\left(\frac{{\tau }_j-{\tau }_t}{h}\right)}{\frac{1}{Th}{\displaystyle \underset{j=k+1}{\overset{T}{\sum }}K}\left(\frac{{\tau }_j-{\tau }_t}{h}\right)}$ ，且 $h>0$ 为核函数 $K(\cdot )$ 的带宽。

将(8)式代入(7)式中的第一个表达式中，可以得到 ${\tilde{r}}_t={\left(c_t;l_t,u_t\right)}_{LR}$ 的估计值 ${\widehat{\stackrel{˜}{r}}}_t={\left({\hat{c}}_t;{\hat{l}}_t,{\hat{u}}_t\right)}_{LR}$ ，具体如下：

$\{\begin{array}{l}{\hat{c}}_t={\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)c_j+{\displaystyle \underset{l=1}{\overset{p}{\sum }}{\alpha }_l}\left(c_{t-l}-{\displaystyle \underset{j=k+1}{\overset{T}{\sum }}{w}_j}\left({\tau }_t\right)c_{j-l}\right),\\ {\hat{l}}_t={\beta }_0+{\beta }_1{l}_{t-1}+{\beta }_2{l}_{t-2}+\cdots +{\beta }_q{l}_{t-q}+{\gamma }_1{\hat{c}}_t,\\ {\hat{u}}_t={\phi }_0+{\phi }_1{u}_{t-1}+{\phi }_2{u}_{t-2}+\cdots +{\phi }_m{u}_{t-m}+{\gamma }_2{\hat{c}}_t,t=k+1,\cdots ,T\end{array}$ (10)

第二阶段中，为了减少异常值的影响，本文采用加权最小二乘法估计未知系数 $\alpha =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_p\right)$ ， $\beta =\left({\beta }_0,{\beta }_1,{\beta }_2,\cdots ,{\beta }_q\right)$ ， $\phi =\left({\phi }_0,{\phi }_1,{\phi }_2,\cdots ,{\phi }_m\right)$ ， $\gamma =\left({\gamma }_1,{\gamma }_2\right)$ ，具体如下：

$\left(\hat{\alpha },\hat{\beta },\hat{\phi },\hat{\gamma }\right)=\underset{\alpha \in {ℝ}^p,\beta \in {ℝ}^q,\phi \in {ℝ}^m,\gamma \in {ℝ}^2}{\arg \min }{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{w}_t}{e}_t$ (11)

其中， $e_t=d^2\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t\right)$ 是 ${\widehat{\stackrel{˜}{r}}}_t$ 和 ${\tilde{r}}_t$ 之间的平方误差距离， $w_t=\frac{1}{1+d^2\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t\right)}$ 是第t个残差对应的权重，由该式可以看出，残差 $e_t$ 越大的时间序列数据得到越低的权重，这样可以减弱异常值对模型的影响。

3.2. 估计模型未知参数的算法

由于提出的模型(7)中，要想估计未知系数和未知光滑函数，就必须确定中心，左展形和右展形的最优滞后阶数 $p_{opt}$ ， $q_{opt}$ 和 $m_{opt}$ 以及最优带宽 $h_{opt}$ ，为此，本文提出了以下迭代算法来确定最优滞后阶数以及最优带宽，进而得到时间序列模型中的未知参数：

步骤1：选择一个核函数，选择一个滞后阶数 $p\in \left\{1,2,\cdots ,P\right\},P\in \mathbb{N}$ ， $q\in \left\{1,2,\cdots ,Q\right\},Q\in \mathbb{N}$ ， $m\in \left\{1,2,\cdots ,M\right\},M\in \mathbb{N}$ ，其中，中心，左展形和右展形的滞后阶数的上限由样本自相关系数决定；

步骤2：假定初始带宽 $h_{\left(0\right)}=0.01$ ；

步骤3：利用初始带宽 $h_{\left(0\right)}$ 和式(10)计算此时未知系数 ${\alpha }_{h_{\left(0\right)}},{\beta }_{h_{\left(0\right)}},{\phi }_{h_{\left(0\right)}},{\gamma }_{h_{\left(0\right)}}$ ；

步骤4：计算CV值，当CV值达到下确界时，此时 $h_{\left(0\right)}$ 即为最优带宽 $h_{opt}$ ，否则，令 $h_{\left(1\right)}=h_{\left(0\right)}+0.01$ ，回到步骤3，重复以上步骤。

$CV\left(h_{\left(0\right)}\right)=\frac{1}{T-k}{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{d}^2}\left({\tilde{r}}_t,{\widehat{\stackrel{˜}{r}}}_t^{h_{\left(0\right)}}\right),$ (12)

其中， ${\widehat{\stackrel{˜}{r}}}_t{}^{h_{\left(0\right)}}$ 是中心，左展形和右展形滞后阶数分别为 $p,q,m$ ，且带宽为 $h_{\left(0\right)}$ 时 ${\tilde{r}}_t$ 的估计值。

步骤5：选择另一组滞后阶数 $p,q,m$ ，其中， $p\in \left\{1,2,\cdots ,P\right\},P\in \mathbb{N}$ ， $q\in \left\{1,2,\cdots ,Q\right\},Q\in \mathbb{N}$ ， $m\in \left\{1,2,\cdots ,M\right\},M\in \mathbb{N}$ ，回到步骤2，并重复以上步骤，模型的拟合优度达到最大时就得了最优的系数估计值。

3.3. 时间序列模型的评价指标

为了评价所提出的基于半参数技术的自适应模糊ARDL时间序列模型的拟合优度，本文使用了一些指标来评价模糊回归模型的性能 [20] [21] ：

$G_1=\frac{{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}\frac{1}{1+E_1\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)}}}{T-k}$ (13)

$MD=\frac{{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}{E}_2}\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)}{T-k}$ (14)

其中，

$E_1\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)={\displaystyle \int \frac{\left|{\widehat{\stackrel{˜}{r}}}_t\left(x\right)-{\tilde{r}}_t\left(x\right)\right|}{{\displaystyle \int {\tilde{r}}_t}\left(x\right)\text{d}x}\text{d}x},$ (15)

$E_2\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)=\frac{1}{2z}{\displaystyle \underset{j=1}{\overset{z}{\sum }}\left(\left|{\widehat{\stackrel{˜}{r}}}_t^L\left[{\alpha }_j\right]-{\tilde{r}}_t^L\left[{\alpha }_j\right]\right|+\left|{\widehat{\stackrel{˜}{r}}}_t^U\left[{\alpha }_j\right]-{\tilde{r}}_t^U\left[{\alpha }_j\right]\right|\right)}.$ (16)

在上述表达式中， ${\alpha }_1<\cdots <{\alpha }_z$ 是[0，1]的任意分区， ${\widehat{\stackrel{˜}{r}}}_t^L\left[{\alpha }_j\right]$ 和 ${\widehat{\stackrel{˜}{r}}}_t^U\left[{\alpha }_j\right]$ 是 ${\widehat{\stackrel{˜}{r}}}_t$ 的 $\alpha$ –水平截集的左端点和右端点。 $G_1$ 越大，说明模糊时间序列模型的观测值与估计值越接近，MD越大，则说明模糊时间序列模型的观测值与估计值的拟合效果越差。

此外，贴近度指标具体形式如下：

$S\left({\widehat{\stackrel{˜}{r}}}_t,{\tilde{r}}_t\right)=\frac{1}{T-k}{\displaystyle \underset{t=k+1}{\overset{T}{\sum }}\frac{Card\left({\widehat{\stackrel{˜}{r}}}_t\cap {\tilde{r}}_t\right)}{Card\left({\widehat{\stackrel{˜}{r}}}_t\cup {\tilde{r}}_t\right)}}$ (17)

其中， $\cap$ 和 $\cup$ 分别表示模糊数空间中的交集算子和并算子， $Card\left(\tilde{A}\right)$ 表示 $\tilde{A}$ 的基数。当贴近度S较大时，说明模糊时间序列模型的观测值与估计值更接近，因此，S越大，说明模型拟合效果越好。

4. 算例分析

本节中，我们考虑1900年至2022年全球陆地–海洋温度指数数据集(见https://data.giss.nasa.gov/gistemp)，来验证所提出模型的可行性和有效性。该数据集包含123个观测时间序列数据。本文使用He et al. [22] 描述的模糊化方法，将全球陆海温度指数转换为三角模糊数，得到模糊时间序列数据。假设存在实数 $c_t$ ，我们可以得到三角模糊数 ${\left(c_t;l_t,u_t\right)}_T$ ， $l_t,u_t$ 可由以下表达式确定：

$P\left\{c_t-l_t<c<c_t\right\}=P\left\{c_t<c<c_t+u_t\right\}=0.05,t=1,2,\cdots ,123,$ (18)

其中，c服从均值为 $\mu$ ，方差为 ${\sigma }^2$ 的正态分布， $\mu =\frac{{\displaystyle \underset{t=1}{\overset{123}{\sum }}{c}_t}}{123}$ ， ${\sigma }^2=\frac{{\displaystyle \underset{t=1}{\overset{123}{\sum }}{\left(c_t-\mu \right)}^2}}{123}$ 。

利用本文提出的半参技术和加权最小二乘法对这些数据进行处理，各残差的权重估计值见表1，由表1可知，该数据集包含3个异常点，分别为第115，第116和第120个数据。

Table 1. Estimated weights in example analysis

表1. 算例分析中的权重估计值

同时，本文与D’Urso [23] ，Li et al. [24] ，Hesamianand Akbari [12] ，Zarei et al. [13] 和Hesamian et al. [18] 提出的模型进行了比较，比较结果见图1。从图1可以看出，在异常值存在的情况下，本文提出的方法获得很好的拟合效果，具有可行性和明显的拟合优势。

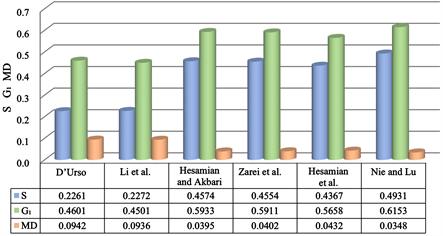
Figure 1. Fitting performances from the models in in example analysis

图1. 算例分析中各模型的拟合指标

5. 总结与展望

在模糊环境中提出的许多统计预测模型依赖于误差平方技术。然而，这种方法在异常数据的存在下可能表现不佳。然而，统计加权可以解决这些缺点。本文提出一种基于半参数技术的自适应模糊ARDL时间序列模型。该模型将数据的变化序列分成中心、左展形和右展形三个部分，以及不确定性大小和模糊程度之间可能存在的关系。本文利用半参数技术建立了自适应回归模型中各元素之间的模糊关系。此外，提出了一种简单有效的加权最小二乘目标来控制异常值，以提高模糊时间序列模型的预测精度。通过与现有模型的比较以及一些常见的拟合优度标准，验证了在异常值存在情况下，所提出模型仍具备可行性和有效性。

在未来的工作中，研究将侧重于改进模糊时间序列的不同稳健算法，如最小中位数平方法、最小截平方和以及切尾绝对偏差等，以优化每个序列的关系分解。在现有模糊关系的基础上，提出了一种新的模糊关系，可以适应各种类型的序列。为了进一步提高预测系统对异常值的稳健性，可以考虑多个异常值的组合。最后，提出的模型也将应用于不同领域的具体问题。

致谢

在此，我要感谢陆老师为改进这篇论文提出的宝贵意见。

NOTES

^*通讯作者。