基于鞅论的时延QoS分析

QoS Signal Delay Analysis Based on Martingale Theory

摘要: 随着网络通信行业的迅速发展，出现了各种各样的数字移动终端，用户对服务质量的要求也不断提高，QoS (Quality of Service)应运而生。时延是QoS的指标之一，通过研究时延可以进一步分析网络的性能。基于排队论，主要研究单一业务到达时的系统性能，建立单一服务器服务的排队系统，在建模中，主要考虑突发性业务，使用突发性到达MMOO过程作为系统的输入，将服务过程建立为ALOHA。利用新的理论方法——鞅论，指数上鞅能够准确描述突发性到达对网络性能的影响，在鞅域中构建服务鞅和到达鞅的结构，通过鞅的停时定理，推导系统的时延违反概率不等式建模出在鞅结构下的时延违反概率界，利用MATLAB统计比较不同的负载率对应的时延违反概率界，发现在突发型的业务到达时，时延界随着负载率的减小更加紧致更加趋于真实值。

Abstract: With the rapid development of network communication industry, various digital mobile terminals have emerged, and users’ requirements for service quality are also constantly improving, QoS (Quality of Service) comes into being. Delay is one of the QoS metrics and the performance of the network can be further analyzed by studying delay. Based on the queuing theory, the system per-formance when a single service arrives is mainly investigated, and establishes the queuing system of a single server service. In the modelling, the bursty service is mainly considered, and the bursty arrival MMOO process is used as the input of the system, and the service process is established as ALOHA. Using a new theoretical approach, the martingale theory, the exponential upper martingale is able to accurately describe the impact of bursty arrivals on network performance, construct the structure of the service martingale and the arrival martingale in the martingale theory, and through the stopping time theorem of the martingale, derive the system’s delay violation probability inequality to model the delay violation probability bounds under the martingale structure. Using MATLAB to statistically compare the delay violation probability bounds corresponding to different load rates, it is found that when bursty traffic arrives, the delay bound becomes tighter and tends to be closer to the true value as the load rate decreases.

1. 引言

随着网络技术的飞速发展，网络从单一的数据网络向集成数据、语音、视频等的多业务网络转变，用户对网络质量的要求也随之增加。时延作为QoS的重要指标，可评价网络性能。文献 [1] 指出传统的分析方法主要基于排队论，当网络规模较大时，存在分析过程复杂、不准确等缺点。由文献 [2] 得由于网络情况比较复杂，排队论需要与其他数学理论结合使用。

上世纪七十年代起，网络队列模型的研究分析中开始引用鞅理论。将排队系统模型中的组成元素利用鞅理论进行建模，然后利用鞅理论的性质分析网络性能。NG Duffield等使用指数鞅建模系统队长并分析系统性质，为日后使用鞅理论分析排队系统性能打下基础，见文献 [3] [4] 。鞅理论是一种重要的随机过程，在现代概率论中经常使用，可以用来描述一类统计期望关于时间变化的随机变量。针对使用鞅理论分析时延的研究，可见文献 [5] - [11] ，Ciucu F, Poloczek F团队创造性的提出了关于鞅的一系建模研究成果以及首次提出鞅包络、到达鞅和服务鞅的概念。其中文献 [8] 中，Ciucu F等利用鞅包络的方法，把业务累计到达过程转化成指数上鞅结构。文献 [10] 中，由于随机网络演算的排队方法并不利于研究，为了避免这种情况，Ciucu F等使用鞅排队来代替，并设置合理的鞅参数和定义队列溢出停时事件。服务鞅理论为不同类型终端到达过程转化成鞅过程提出了全新的方法，具体可见文献 [11] 。文献 [12] 对无线资源进行有效的切片管理。通过构建每个切片上到达过程的超鞅，证明基于鞅理论为业务提供的统计型QoS保障可以使得排队系统性能概率界更加紧致。由于现实中的业务流量具有复杂性和突发性，可将业务的流量建模为马尔可夫调制过程，文献 [13] 证明在鞅理论的SFC逐跳带宽方案下，得到的时延违反概率界优于基于EB/EC理论所得。综上，到达鞅和服务鞅等鞅理论为时延可靠性分析框架提供了全新思路。

本文基于统计型QoS保障，在排队论的基础上研究分析突发性情况下的系统特性，并与鞅论相结合，针对指定的到达与服务模型提供了精确的可靠性分析保障框架。到达选择马尔可夫，调制机制选择Aloha。利用鞅的停时定理推导时延违反概率，仿真不同负载率下的鞅论时延违反概率界。

2. 理论基础

2.1. 排队论和排队基础

排队论是一个独立的数学分支，是专门研究由于随机因素的影响而产生的拥挤现象(排队、等待)的科学，也称为随机服务系统理论或拥塞理论(Congestion Theory)。排队论是对通信网内的流量进行分析的数学工具。利用排队论中的ErlangB公式和ErlangC公式以及鞅论，就可以计算出网络的呼损和时延，用它们来评估通信网的性能。在通信时间内，对用户提供良好的服务，需要有足够的线路(信道)容量。线路容量不够，将导致拥塞现象，出现“排队问题”，本文利用排队系统来描述这一问题。本文中建立包级别的排队系统，即终端用户的数据以数据包的形式到达系统，等待服务，如图1所示。

Figure 1. Queueing system

图1. 排队系统

1) 到达：终端业务的到达过程是可以用各种不同分布来建模的随机过程。根据不同的业务数据包到达方式，有一般突发性低的周期性发包业务和紧急事件触发的突发性较强的业务，本文主要研究后者，建模为MMOO过程。

2) 排队：排队系统分为两种：拒绝系统和非拒绝系统。在拒绝系统中，根据系统允许的排队队长和窗口数的大小关系，又分为即时拒绝和延时拒绝。非拒绝系统，即系统允许的排队队长没有限制，当数据包到达且没有空余窗口时，数据包加入排队行列等待服务，也由此产生了时延。

3) 服务：本文采用先到先服务，服务过程为伯努利，作为拓展，加入了在ALOHA接入机制下网络的时延性能。

4) 离去：离去过程是一个随机过程，与到达过程和服务过程均有联系。

2.2. 队长

队长全称排队长度，是在某时刻系统内滞留的数据包数量和正在被服务的数据包数量。队长的定义如下：

$Q\left(n\right)=\underset{n\ge 0}{\sup }\left\{A_i\left(n\right)-S\left(n\right)\right\}$ (1)

其中 $Q\left(n\right)$ 是队长， $A_i\left(n\right)={\displaystyle {\sum }_{i=1}^{n}a\left(i\right)}$ ，为n时刻的累计到达， $S\left(n\right)={\displaystyle {\sum }_{i=1}^{n}s\left(i\right)}$ ，为n时刻的累计服务。

2.2.1. QoS简介

所谓网络QoS，即服务质量(Quality of Service)，是网络在其传输数据流时需要满足的一系列的服务请求，也是服务性能的反映，是一种综合性指标，主要取决于用户对服务性能的满意程度的总体表现。

时延是QoS的重要指标，是指将数据包从发送端传输到接收端的时间，本文主要使用虚时延理论。虚时延定义如下：

$W\left(n\right)=\min \left\{k\ge 0|A\left(n-k\right)\le D\left(n\right)\right\}$ (2)

其中，D(n)为系统离去过程，虚时延可以理解为进入缓存排队中的数据经历的系统服务，直到离去所需的最少时间

2.2.2. QoS保障

QoS服务可分为确定性QoS、统计型QoS以及“尽力而为”型QoS。其中“尽力而为”型QoS最简单，在该类型下的QoS不为网络系统中的信息传输提供任何QoS指标保证，通常使用在对时延等级要求不高的通信系统中。

本文主要使用统计型QoS。即对承诺的QoS服务在允许在一定范围内波动，但是不会造成不良后果。与确定型服务的“硬”保证不同，统计型服务提供QoS“软”保证，它允许对通信各方已协商好的各项QoS参数值有一定程度的违反。

基于大偏差理论，在稳态遍历到达和服务过程的排队系统中，队列长度 $Q\left(n\right)$ 收敛至 $Q\left(\infty \right)$ 。

2.3. 鞅理论

2.3.1.鞅理论的定义与基本性质

鞅理论其实是一种重要的随机过程，在现代概率论中经常使用。起初人们常用“公平赌博”来直观诠释“鞅”，假设赌局是公平的，也就是输赢概率各半。此时，下一步损失的期望值就等于赌徒当前的损失，所以。当一个人参加n轮赌博后，继续第n + 1轮时，若他在第n轮结束后所剩赌资 $X_n$ 与第n + 1轮赌资的均值相等，即第n + 1轮不输也不赢，则可以称这种赌博在统计学角度上是公平的。

由于鞅是一种特殊的随机过程，所以常用数学条件期望来描述。假设已知当前n时刻之前的全部信息，若随机过程n时刻的值等于n + 1时刻的条件期望，则可称此随机过程为鞅，用数学可表示为：

定义1 (离散时间鞅)：假设有随机过程 $\left\{X_n,n\ge 0\right\}$ ，若满足：

1) $E\left|X_n\right|<\infty$ ；

2) $E\left[X_{n+1}|X_0,\cdots ,X_n\right]=X_n$

则过程 $\left\{X_n,n\ge 0\right\}$ 称为鞅。有时 $X_n$ 不能直接观察，只能观察另一个过程 $\left\{Y_n,n\ge 0\right\}$ ，因此将鞅的定义进行推广。

定义2 (离散时间鞅)：设两个随机过程 $\left\{X_n,n\ge 0\right\}$ ， $\left\{Y_n,n\ge 0\right\}$ ，若满足：

1) $E\left|X_n\right|<\infty$ ；

2) $E\left[X_{n+1}|Y_0,\cdots ,Y_n\right]=X_n$

则称 $\left\{X_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是鞅，即已知n时刻以及之前的值 $X_0,X_1,\cdots ,X_n$ ，于是可以得出 $n+1$ 时刻的值 $X_{n+1}$ 对 $X_0,X_1,\cdots ,X_n$ 的条件期望与 $X_0,X_1,\cdots ,X_{n-1}$ 无关，只和 $X_n$ 有关且等于 $X_n$ 。针对这种特殊的随机过程——鞅，有以下几种性质：

1) 性质1： $E\left[X_n|Y_0,\cdots ,Y_n\right]=X_n$ ，再推广可以有 $E\left[X_{n-k}|Y_0,\cdots ,Y_n\right]=X_{n-k},k\ge 0$

2) 性质2： $E\left[X_{n+k}|Y_0,\cdots ,Y_n\right]=X_{n+k},k\ge 0$ ，则 $E{X}_{n+1}=E{X}_n=E{X}_0$ ，此性质在鞅的应用过程中最常见；

3) 性质3：若 $\left\{X_n,n\ge 0\right\},\left\{Z_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是鞅且相互独立，则随机过程 $\left\{X_n{Z}_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是鞅，此性质常用于随机过程的鞅构造。

2.3.2. 鞅的举例与构造方法

为了能进一步了解并运用鞅理论，现举例说明：

若 $Y_0=0$ ， $\left\{Y_n,n\ge 1\right\}$ 独立同分布， $E\left|Y_n\right|<\infty$ ， $E{Y}_n=0$ ，取 $X_0=0$ ， $X_n={\displaystyle {\sum }_{i=1}^n{Y}_i}$ ，则 $\left\{X_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是鞅。若 $\left\{Y_n\right\}$ 为Markov链，状态空间为 $\mathcal{S}$ ，转移矩阵为P，定义 $F=\left(f\left(0\right),\cdots ,f\left(i\right),\cdots \right)$ 为右特征向量， $E\left|f\left(Y_n\right)\right|<\infty$ 。令 $X_n={\lambda }^{-n}f\left(Y_n\right)$ ，则 $\left\{X_n\right\}$ 关于 $\left\{Y_n\right\}$ 是鞅。

证明： $E\left|X_n\right|={\lambda }^{-n}E\left|f\left(Y_n\right)\right|<\infty$ ，

$E\left[X_{n+1}|Y_0,\cdots ,Y_n\right]=E\left[{\lambda }^{-n-1}f\left(Y_{n+1}\right)|Y_n\right]={\lambda }^{-n-1}{\sum }_{j\in S}f\left(y_i\right)P\left(Y_{n+1}=y_j|Y_n\right)={\lambda }^{-n}f\left(Y_n\right)$ 。

2.3.3. 上鞅、下鞅的定义及基本性质

定义3：随机过程 $\left\{X_n,n\ge 0\right\},\left\{Y_n,n\ge 0\right\}$ 满足下列条件：

$E\left[X^{-}\right]>\infty ,x^{-}=\min \left(x,0\right)$

$E\left[X_{n+1}|Y_0,\cdots ,Y_n\right]\le X_n$ (3)

$X_n$ 是 $Y_0,\cdots ,Y_n$ 的函数

则称 $\left\{X_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是上鞅，且由上鞅的定义可知上鞅满足单调递减，同理(3)可定义下鞅。

下面是上(下)鞅的一些重要性质：

性质1：上鞅 $\left\{X_n,n\ge 0\right\}$ ，则 $E\left[X_{n+k}|Y_0,\cdots ,Y_n\right]\le X_n,\forall k\ge 0$ ；

性质2：上鞅 $\left\{X_n,n\ge 0\right\}$ ，则 $E{X}_n\le E{X}_k\le E{X}_0,n\le k\le n$ ，上鞅在0时刻的期望值取最大，所以在许多关于上鞅的不等式证明过程中都会使用到0时刻的期望值；

性质3：若随机过程 $\left\{X_n,n\ge 0\right\},\left\{Z_n,n\ge 0\right\}$ 都关于 $\left\{Y_n,n\ge 0\right\}$ 是上鞅，且随机过程 $\left\{X_n,n\ge 0\right\},\left\{Z_n,n\ge 0\right\}$ 相互独立，则 $\left\{X_n{Z}_n,n\ge 0\right\}$ 关于 $\left\{Y_n,n\ge 0\right\}$ 是上鞅，此性质可用于随机过程的上鞅构造。

2.4. 停时和停时理论

为了可以进一步了解鞅论，下面引进鞅的停时与停时定理。

鞅的停时：令 $F_n=\sigma \left(X_k,0\le k\le n\right)$ ， $F_n$ 表示随机变量 $X_0,X_1,\cdots ,X_n$ 可提供的全部信息，称为 $X_0,X_1,\cdots ,X_n$ 生成的 $\sigma$ 域。设有非负随机变量 $\tau$ 和随机序列 $\left\{X_n,n\ge 0\right\}$ ，若 $\forall n\ge 0,\left\{\tau =n\right\}\in F_n$ 则称 $\tau$ 是 $\left\{X_n,n\ge 0\right\}$ 的停时。其中，若 $\tau$ 是一个停时 $\forall n\ge 0,\left\{\tau =n\right\}\in F_n$ ，那就可以导出事件 $\left\{\tau \le n\right\},\left\{\tau >n\right\},\left\{\tau \ge n\right\},$ $\left\{\tau <n\right\}$，且这些事件均只由 $X_0,X_1,\cdots ,X_n$ 确定，即截止到n时刻，根据已有的信息可以完全确定停时所对应的事件是否已经发生。

停时定理1：令 $\left\{X_n,n\ge 0\right\}$ 是鞅， $\tau$ 是停时，当

$P\left(\tau <\infty \right)=1$

$E\left|X_{\tau }\right|<\infty$ (4)

$\underset{n\to \infty }{\lim }E\left|X_n{I}_{\left\{\tau >n\right\}}\right|=0$

成立时，则 $E{X}_{\tau }=E{X}_0$ ，由于公式(4) $E\left|X_{\tau }\right|<\infty$ 对停时点T的均值 $E\left|X_{\tau }\right|$ 的存在有限制作用，现推导出停时定理2。

停时定理2：令 $\left\{X_n,n\ge 0\right\}$ 是鞅， $\tau$ 是停时，当

$P\left(\tau <\infty \right)=1$

$E\left[\underset{n\ge 0}{\sup }\left|X_{t\wedge \tau }\right|\right]<\infty$ (5)

成立时， $E{X}_{\tau }=E{X}_{t\wedge \tau }=E{X}_0$ ，其中 $E\left[\underset{n\ge 0}{\sup }\left|X_{t\wedge \tau }\right|\right]<\infty$ 是停时定理1的增强型条件，该停时定理在证明过程中经常使用。

3. 基于鞅论的时延分析

本文研究的到达过程选用MMOO过程，服务过程选择ALOHA机制建模为伯努利。建立MMOO到达的排队系统模型，采用ALOHA机制，利用鞅论进行分析，得到对应的时延违反概率。其中，使用鞅理论对概率域上的随机过程转换时，得到其对应的在鞅域中的“服务鞅”和“到达鞅”。

3.1. 到达鞅和服务鞅

定义1 (到达鞅)在到达过程A中，对于任意 $\vartheta >0$ ，都对应的 $K_a\ge 0$ 和函数 $h_a:rng\left(a\right)\to R^{+}$ ，得到到达过程 $A\left(n\right)$ 在鞅域中对应的到达鞅：

$h_a\left(a\left(n\right)\right){\text{e}}^{\vartheta \left(A\left(n\right)-n{K}_a\right)},n\ge 0$ (6)

其中， $a\left(n\right)$ 表示瞬时到达， $rng(·)$ 表示瞬时到达， $A\left(n\right)$ 表示累积到达， $\vartheta$ 代表衰减指数，决定参数 $K_a$ 和 $h_a$ 。

定义2 (服务鞅)在服务过程S中，对于每一个 $\vartheta >0$ ，都对应 $K_s\ge 0$ 和 $h_s:rng\left(s\right)\to R^{+}$ ，得到服务过程 $S\left(n\right)$ 在鞅域中对应的服务鞅：

$h_s\left(s\left(n\right)\right){\text{e}}^{\vartheta \left(n{K}_s-S\left(n\right)\right)},n\ge 0$ (7)

其中， $s\left(n\right)$ 表示瞬时服务， $S\left(n\right)$ 表示累计服务， $\vartheta$ 决定参数 $K_s$ 和 $h_s$ 。

3.2. 随机过程的鞅变换

本文用MMOO过程来建模到达服务，MMOO到达的马尔可夫链如图2所示。

Figure 2. MMOO model

图2. MMOO模型

当系统为ON状态时到达速率为R，Off状态时无数据到达。pa表示Off到On的转变概率，qa表示On状态到Off状态的转变概率。此马尔科夫链状态空间 $S=\left\{0,1\right\}$ ，其对应的概率转移矩阵T与对角速率矩阵∆为：

$T=\left[\begin{array}{cc}1-pa& pa\\ qa& 1-qa\end{array}\right]$ ， $\Delta =\left[\begin{array}{cc}0& \\ & R\end{array}\right]$ (8)

根据到达鞅定义，可将MMOO过程的鞅构造为：

$M_a\left(n\right)=h_a\left(a\left(n\right)\right){\text{e}}^{\vartheta \left(A\left(n\right)-n{K}_{ai}\right)}$ (9)

其中 $h_a$ 表示对应的右特征向量， $sp\left(T^{\vartheta }\right)$ 表示谱半径。

当MMOO过程建模为到达鞅时，系统的累计到达 $A_i\left(n\right)={\displaystyle {\sum }_{k=0}^{n}f\left(x_k\right)}$ 。为了保证到达鞅满足指数上鞅的要求，需确保下式成立：

$E\left[h_{ai}\left(x_{n+1}\right){\text{e}}^{\vartheta \left(A_i\left(n+1\right)-\left(n+1\right)K_{ai}\right)}|x_1,\cdots ,x_n\right]=h_{ai}\left(x_n\right){\text{e}}^{\vartheta \left(A_i\left(n\right)-n{K}_{ai}\right)}$ (10)

指数列变换矩阵 $T^{\vartheta }$ 可表示为：

$T^{\vartheta }=\left[\begin{array}{cc}1-pa& pa{\text{e}}^{\vartheta R}\\ qa& \left(1-qa\right){\text{e}}^{\vartheta R}\end{array}\right]$ (11)

则MMOO的到达鞅参数 $K_{ai}$ 的定义为：

$K_{ai}=\frac{\log sp\left(T^{\vartheta }\right)}{\vartheta }$ (12)

若服务是MMOO过程，根据服务鞅定义为：

$M_s\left(n\right)=h_s\left(s\left(n\right)\right){\text{e}}^{\vartheta \left(n{K}_s-S\left(n\right)\right)}$ (13)

为保证服务鞅满足指数上鞅要求，服务鞅也需满足下式定义：

$E\left[h_s\left(x_{n+1}\right){\text{e}}^{\vartheta \left(\left(n+1\right)K_s-S\left(n+1\right)\right)}|x_1,\cdots ,x_n\right]=h_s\left(x_n\right){\text{e}}^{\vartheta \left(n{K}_s-n{K}_s\right)}$ (14)

与到达鞅同理，此时的指数列变换矩阵 $T^{\vartheta }$ 为：

$T^{\vartheta }=\left[\begin{array}{cc}1-pa& pa{\text{e}}^{-\vartheta R}\\ qa& \left(1-qa\right){\text{e}}^{-\vartheta R}\end{array}\right]$ (15)

则服务鞅参数 $K_s=\frac{\log sp\left(T^{\vartheta }\right)}{\vartheta }$

3.3. 基于鞅的时延违反概率

根据上鞅的性质，两个上鞅过程的乘积还是上鞅过程。因为服务鞅和到达鞅均是上鞅结构，已知队长为 $Q\left(n\right)=\underset{n\ge 0}{\sup }\left\{A_i\left(n\right)-S\left(n\right)\right\}$ ，所以构造出队列长度的鞅：

$M^L\left(n\right)=h_{ai}\left(a_i\left(n\right)\right)h_s\left(s\left(n\right)\right){\text{e}}^{{\vartheta }^{*}\left(A_i\left(n\right)-S\left(n\right)+n{K}_s-n{K}_{ai}\right)}$ (16)

其中

${\vartheta }^{*}=\sup \left\{\vartheta >0:K_{ai}\le K_s\right\}$ (17)

当 ${\vartheta }^{*}$ 取极值时有 $K_{ai}=K_s$ ，则队长 $M^L\left(n\right)$ 化简为：

$M^L\left(n\right)=h_{ai}\left(a_i\left(n\right)\right)h_s\left(s\left(n\right)\right){\text{e}}^{{\vartheta }^{*}\left(A_i\left(n\right)-S\left(n\right)\right)}$ (18)

根据鞅的停时理论：在鞅过程中，在停时时刻的期望小于或等于其初值的期望，由此可得时延违反概率界：

$P\left(Q>\sigma \right)\le \frac{E\left[h_{ai}\left(a_i\left(0\right)E\left[h_s\left(s\left(0\right)\right)\right]\right)\right]}{H}{\text{e}}^{-{\vartheta }^{*}\sigma }$ (19)

其中 $\sigma$ 为系统队长的阈值，H是阈值，由下式确定：

$H=\min \left[h_{ai}\left(x\right)h_s\left(y\right):x-y>0\right]$ (20)

当 $N=\infty$ 时，有 $P\left(N<\infty \right)=P\left(Q>\sigma \right)$ 。停止时间N第一次超过 $\sigma$ 表示为：

$N=\min \left[n:A_i\left(n\right)-S\left(n\right)\ge \sigma \right]$ (21)

根据停时理论和文献 [8] 得下式：

$\begin{array}{c}E\left[M^L\left(0\right)\right]=E\left[h_{ai}\left(a_i\left(0\right)\right)\right]E\left[h_s\left(s\left(0\right)\right)\right]=E\left[M^L\left(N\wedge n\right)\right]\ge E\left[M^L\left(N\wedge n\right)1_{\left\{N\wedge n\right\}}\right]\\ =E\left[h_{ai}\left(a_i\left(N\right)\right)h_s\left(s\left(N\right)\right){\text{e}}^{{\vartheta }^{*}\left(A_i\left(N\right)-S\left(N\right)\right)}{1}_{\left\{N\le n\right\}}\right]\ge H{\text{e}}^{{\vartheta }^{*}\sigma }P\left(N\le n\right)\end{array}$ (22)

4. 仿真结果与分析

1) 图3为Matlab仿真的系统到达是MMOO过程，服务为伯努利业务流，负载率 $\rho =0.55,0.7,0.9$ 时的时延违反概率仿真结果。

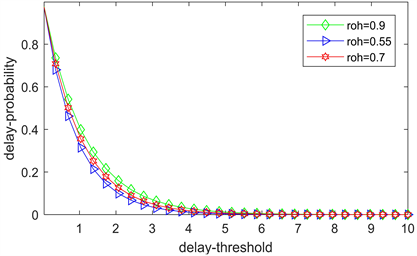
Figure 3. Probability of delay violation under different load rates

图3. 不同负载率下的时延违反概率

由图可知，负载率越大，时延违反概率也越大，对网络的影响也随之增加。

2) 图4为引入了ALOHA机制下仿真生成的MMOO流的时延违反概率，负载率 $\rho =0.55,0.7$ 。在ALOHA机制下时延违反概率界同样随着负载率的减小而紧致，且更加接近实测值。

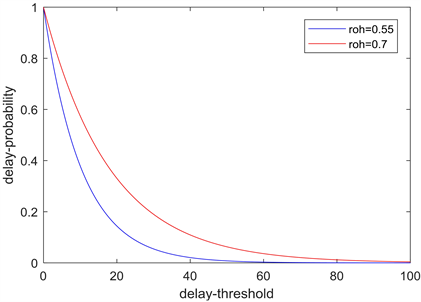
Figure 4. Delay violation under Aloha mechanism

图4. ALOHA机制下的时延违反

3) 为了进一步证实鞅理论有望成为网络性能评估与分析的新理论，图5是图4的延伸，ALOHA机制下仿真生成的MMOO流的时延违反概率，利用鞅理论和EB-EC两个理论，负载率仍选择 $\rho =0.55$ 。

Figure 5. Comparison of two theories

图5. 两种理论对比

由图可知，在同一负载率的情况下，鞅理论得出的时延违反概率明显优于EC-EC推导的时延违反概率，即利用鞅理论推导的时延界更加紧致

综上，在鞅域中，时延界随着负载的减小更加紧致，且在同一负载率下鞅理论推导的时延违反概率要比EB-EC理论推导的紧致，更加接近实测值。

参考文献

NOTES

^*通讯作者。