1. 引言
设
为给定的正整数,并且满足
,对于不定方程
的正整数解研究已经有了诸多进展。对于
的情形,Chon [1] 在1971年证明了当
时,上述不定方程仅有一组正整数解
;Ponnudurai [2] 在1975年证明了当
时,上述不定方程仅有两组正整数解
;宣体佐 [3] 在1982年证明了当
时,上述不定方程仅有一组正整数解
;Luo [4] 在2001年证明了当
时,上述不定方程仅有一组正整数解
。对于
的情形,曹珍富 [5] 在1982年证明了当
时,上述不定方程仅有一组正整数解
;罗明,朱德辉和马芙蓉 [6] 在2009年证明了当
时,上述不定方程仅有一组正整数解
。
实际上,近年来仍有许多学者关注上述不定方程的正整数解问题并给出了许多结论,特别关于
的情形。胡邦群和罗明 [7] 在2017年证明了当
时,上述不定方程仅有一组正整数解
,以及当
和
时,上述不定方程均无正整数解;李妮 [8] 在2017年当
时,上述不定方程无正整数解;杨晓柳和牟全武 [9] 在2018年证明了当
时,上述不定方程仅有一组正整数解
;林丽娟 [10] 在2021年证明了当
时,上述不定方程仅有一组正整数解
;王润青 [11] 在2021年证明了当
时,上述不定方程仅有一组正整数解
。
不定方程求解的困难性导致有相当一部分不定方程的正整数解是未知的,特别是当
时,上述方程的求正整数解问题仍未解决。本文将证明
时,即不定方程
(1)
无正整数解。本文的主要结果进一步完善了当
并且p和q互素时,不定方程求正整数解的相关结论。
2. 预备知识
首先,我们将方程(1)化简为:
,
此时令
,
,方程(1)就转化为
。
参照文 [12] 可知,方程
的全部整数解可由以下两个结合类(非歧类)给出
,
,
其中
是方程
的相应结合类的基本解,
是Pell方程
的基本解。
由于上述结合类
与
是共轭的,即
。因此,如果y是方程(1)的一个整数解,则应满足
,其中
,即
。 (2)
显然(2)式可以写成以下两个等式:
; (3)
。 (4)
下面我们将证明当且仅当
时(3)式成立,当且仅当
时(4)式成立。从而给出不定方程(1)的全部整数解,并证明该不定方程无正整数解。
根据上面所给出的结合类的关系式,不难推导出下列关系式成立:
; (5)
; (6)
; (7)
; (8)
; (9)
; (10)
; (11)
。 (12)
3.
本节将证明当且仅当
时(3)式成立,即当且仅当
时
为平方数。
引理1 若
为平方数,则必需
。
证明 根据(7)式,我们对递归序列
取模7,其剩余类序列周期为3,当
时,
,此时
。因为
(其中
表示a对p的Jacobi符号),因此当
时,
不可能是平方数,从而排除
。此时还剩下
的情况未讨论这等价于
。
在下面的证明过程中,我们会使用同样的方法去证明
在某些情况下不为平方数,为节省篇幅,叙述方式会稍微简略。
下证当
时,
不为平方数。首先,对
取模1801,其剩余类序列周期为15,当
时,
。其次,对
取模29,671,其剩余类序列周期为15,当
时,
。此时,还剩下
的情况未讨论,这等价于 。
。
下证当
时,
不为平方数。对
取模67,其剩余类序列周期为6,当
时,
,从而排除
,这等价于排除
。此时,还剩下
$$的情况未讨论,这等价于
。
下证当
时,
不为平方数。对
取模61,其剩余类序列周期为60,当
时,
。此时,还剩下
的情况未讨论。
下证当
时,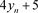 不为平方数,这等价于排除
。首先,对
取模887,其剩余类序列周期为8,当
时,
,从而排除
,这等价于排除
。其次,对
取模719,其剩余类序列周期为48,当
时,
,从而排除
,这等价于排除
。最后,对
取模544543,其剩余类序列周期为32,当
时,
,从而排除
,这等价于排除
。至此,可以排除
,还剩下
的情况未讨论,这等价于
不为平方数,这等价于排除
。首先,对
取模887,其剩余类序列周期为8,当
时,
,从而排除
,这等价于排除
。其次,对
取模719,其剩余类序列周期为48,当
时,
,从而排除
,这等价于排除
。最后,对
取模544543,其剩余类序列周期为32,当
时,
,从而排除
,这等价于排除
。至此,可以排除
,还剩下
的情况未讨论,这等价于
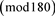 。
。
下证当
时,
不为平方数。首先,对
取模541,其剩余类序列周期为180,当
时,
。其次,对
取模2161,其剩余类序列周期为45,当
时,
,从而排除
,这等价于排除
。最后,对
取模19,其剩余类序列周期为18,当
时,
,从而排除
,这等价于排除
。
至此,仅剩下
的情况未讨论。证毕。
引理2 如果
,则有
。
证明 如果
,根据递归序列(5)可知
,即有
,
,从而立即有
,
,
并且结合递归序列(6)可知
,因此我们有
,
,
再由等式(8)可得
。
于是我们根据等式(8)有
证毕。
引理3 如果
,则仅当
时,
为平方数。
证明 当
时,
。
当
且
时,令
,其中
,
(即
)。如果m取
,
,
中之一,那么由(9)式和(12)式可得
,
再由引理2可得
。
根据递归序列(5)和(6),对
取模521,所得到的两个剩余类序列周期均为65,而对
取模65,其剩余类序列的周期为12。下面对n分成以下两种情况讨论。
情况1:当
时。此时若
,则令
;若
,则令
;若
,则令
。
根据(9)式,(12)式以及引理2可得
,
此时,我们有表1:

Table 1. When k ≡ 1 ( mod 4 ) , t, m, and 24 v m + 5 u m correspond to tables
表1.
时,t,m以及
对应表
对表1中的所有m均有
,故在情况1中
不为平方数。
情况2:当
时。此时若
,则令
;若
,则令
;若
,则令
。
根据(9)式,(12)式以及引理2可得
,
此时,我们有表2:

Table 2. When k ≡ − 1 ( mod 4 ) , t, m, and − 24 v m + 5 u m correspond to tables
表2.
时,t,m以及
对应表
对表2中的所有m均有
,故在情况2中
不为平方数。证毕。
引理4 如果
,则仅当
时,
为平方数。
证明 当
时,
。
当
且
时,令
,其中
,
。如果m取
以及
中之一,那么由(7)式和(12)式可得
,
又因为
,根据递归序列(5)可知
,即有
,
,
因此,我们有
。
根据递归序列(5),对
取模53,其剩余类序列周期均为52,而对
取模52,其剩余类序列的周期为12。此时若
,则令
;若
,则令
。此时,我们有表3:

Table 3. t, m, and um correspond to tables
表3. t,m以及um对应表
当
时,则有
,此时由(5)式可得,
。对此m和表3中的所有m均有
,从而
不为平方数。证毕。
4.
引理5
为平方数仅当
时成立。
证明 由递归序列(7)可知,当
时,
,此时
不可能是平方数;当
时,
。证毕。
5. 主要结论
根据前几节的讨论,可以得出本文的主要结论。
定理1 不定方程(1)的全部整数解为
其中无正整数解。
证明 在前几节的讨论中,我们将求不定方程(1)的全部整数解的问题转化成对
在n取何值时是平方数的讨论。
根据引理1,引理3以及引理4可知,(3)式成立当且仅当
,即
为平方数当且仅当
。当
时,
,此时给出不定方程(1)的一组整数解,即
,
。当
时,
,此时
,将其带入不定方程(1)的化简形式中,则有
,经计算方程
不存在整数解。
根据引理5可知,(4)式成立当且仅当
,即
为平方数当且仅当
。当
时,
,此时给出不定方程(1)的一组整数解,即
,
。
综上,我们给出了不定方程(1)的16组整数解,且无正整数解。证毕。
6. 结语
本文延续了文献 [6] 的证明思路,将不定方程(1)等价转化成Pell方程(2),并构建出方程(1)和方程(2)的整数解的等价关系,并通过运用递归序列、平方剩余等初等方法,得出方程(2)的全部整数解,继而得到方程(1)的全部整数解,从而证明不定方程(1)无正整数解。
事实上,不同类型的不定方程的递归序列具有不同的特点,我们在证明过程中需要结合本文所研究的不定方程的递归序列的特点转换研究思路,这其中包括选择
而不是
。本文的主要结果(即定理1),进一步完善了当
并且p和q互素时,关于这种类型的不定方程求正整数解的相关结论。但是对于上述类型的不定方程,还有问题值得进一步研究,即是否能给出求解公式,从而简化上述类型的不定方程的正整数解的求解过程。
参考文献