基于重构残差保持的深度矩阵分解的多视图聚类

Multi-View Clustering Based on Deep Matrix Factorization with Local Residual Preserving

摘要: 多视图聚类是机器学习中的一个基本问题，近年来，基于矩阵分解用于学习多视图数据获得广泛的关注，并且取得了不错的效果。然而，我们发现现有的多视图聚类方法大多主要关注多视图数据所蕴含的重要属性，即一致性和互补性，而忽略了属于单个视图的特定统计属性。为此，本文提出一个矩阵深度矩阵分解的局部残差保持的多视图聚类算法(LRPDMF)，我们通过图嵌入的方式，捕捉到每个视图的特定统计属性，保证每一层的数据重构，相似的数据点具有相似的重建残差。在融合阶段的，我们利用这些学习到的特征，由于不同的视图可能会有不同的权重，我们利用自适应的方式将他们逼近到一个相似低维空间。在不同的数据集上，我们的LRPDMF与现在最先进的方法比较，获得不错的实验效果。

Abstract: Multi-view clustering is a fundamental problem in machine learning, and in recent years, the use of matrix factorization-based for learning multi-view data has gained widespread attention and achieved good results. However, we find that most of the existing multi-view clustering methods mainly focus on the important attributes embedded in multi-view data, i.e., consistency and complementarity, while ignoring the specific statistical properties belonging to individual views. To this end, in this paper, we propose a local residual preserving multi-view clustering algorithm with deep matrix factorization (LRPDMF), where we capture the specific statistical properties of each view by means of graph embedding, which ensures that the data is reconstructed at each layer and similar data points have similar reconstructed residuals. In the fusion phase, we utilize these learned features, and since different views may have different weights, we approximate them to a similar low-dimensional space using an adaptive approach. On different datasets, our LRPDMF obtains good experimental results when compared with the state-of-the-art methods.

1. 引言

在海量的数据中，如何挖掘到准确有效的数据成为机器学习关注一个重点。而无监督聚类是数据挖掘中一种有效的方法，它的目标是将具有相似属性的数据点分到相同的簇中。但寻找数据之间的相似性仍然是一个具有挑战性的问题。传统的聚类只是从单一视图获得聚类结果，但是面对数据激增的情况下，单单从单一试图获得聚类结果已经缺乏一些广泛使用的场景。一些研究也表明，与从单一视图中提取信息相比，从多视图中提取信息可以获得精确的聚类结果 [1] 。在这个大数据集时代，如何学习到准确的多视图信息变得尤为重要。

多视图学习问题的解决方案包括协同训练、多核学习(MKL)、图学习和子空间学习 [2] 。最早解决多视图学习问题的方法是协同训练 [3] 。通过交替训练未标记数据上的两个视图，协同训练可以最大限度地提高两个视图之间的相互一致性。联合训练在半监督学习和聚类中取得了巨大成功。MKL用于多视图学习 [4] 。MKL中的每个内核自然对应一个视图，不同内核的组合可以是线性或非线性，这两种方式都能提高学习性能。基于图的多视图学习方法是为每个视图构建一个图，并通过图融合使用多个视图的信息进行学习 [5] [6] 。对于基于子空间学习的多视图学习问题，我们假定每个视图都由一个潜在子空间生成，然后我们需要找到不同视图共享的潜在空间的表示 [7] 。基于子空间的学习方法应用于多视图学习有一个优势。潜在子空间的维度通常低于任何输入的维度，因此可以在一定程度上消除“维度诅咒”问题。获得潜在子空间后，所有视图都会被投射到这个子空间中，从而共同完成所需的任务。

近年来，矩阵分解也是一种常见的降维方法，近年来，用于多视图聚类的矩阵方法也取得了很不错的效果。Liu等人 [1] 提出了联合的非负分解矩阵的多视图聚类算法，不同视图生成一个不同的编码矩阵，约束不同视图的编码矩阵趋向一致，生成一个共享的编码矩阵。Liang等人 [8] 通过对基础矩阵和编码矩阵施加正交约束，可以很好地学习每个视图的信息多样性。单层的矩阵分解已经不能很好地学习到准确的特征，Trigeorgis等人 [9] 首次提出了深度矩阵分解，相比于单层的矩阵分解，深度矩阵分解能够更好地挖掘数据的潜在信息。Zhao等人 [10] 将深度矩阵分解用到多视图聚类当中，在最后一层的分解中，还利用图结构学习更抽象的特征。Li等人 [11] 提出了图约束的深度矩阵分解的多视图聚类算法，并对每一层的分解都加上图约束，更好地学习到了每个视图的特征。

但我们发现这些方法忽略了属于单个视图的特定统计属性。所以，我们提出了一个基于局部残差保持的深度矩阵分解的算法。为了能够保持每个视图的特有属性，我们用到了图嵌入的方法，确保每一个相似点能够分配到相似的重构残差。换句话说，在分解的过程中局部残差的保持有利于学到每个视图的特有属性。在融合策略上，我们将最后一层分解的矩阵，用自适应的方式强制集中起来，寻找到一个更加准确的潜在空间。

本篇文章的主要贡献点为：(1) 提出了局部残差保持与深度矩阵分解，并应用在多视图聚类中。(2)提出了一种新的融合策略，能更好地学习不同视图的信息。(3) 本文提出的方法与现有最先进的方法进行比较，取得了不错的效果，证明我们的方法是有效的。

2. 相关工作和基础知识

2.1. 注释

本文中的矩阵用大写字母表示。对于矩阵A，第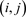个元素表示为 $A_{ij}$ 。我们将 $A\in {\Re }^{m\times n}$ 表示数据矩阵，其中m表示特征维度，n表示实例数。 ${\Vert A\Vert }_F$ 表示矩阵A的Frobenius范数， $A^{\text{T}}$ 表示矩阵A的转置， $tr\left(A\right)$ 表示矩阵A的迹。I表示单位矩阵。

2.2. 深度半非负矩阵分解

在许多情况下，我们需要分析的数据是会相当复杂化，而单层的矩阵分解已经不能很好地完成任务。Trigeorgis等人 [9] 首次提出了深度半非负矩阵(Deep Semi-NMF)的方法，与单层矩阵分解，深度半非负矩阵分解能够更好地表示这些复杂的数据。对于数据我们可以由以下分解：

$\begin{array}{l}{Q}_{l-1}\approx P_l{Q}_l\\ ⋮\\ Q_2\approx P_3\cdots P_l{Q}_l\\ Q_1\approx P_2\cdots P_l{Q}_l\end{array}$ (1)

其中l是层数。我们利用F范数Deep Semi-NMF构建损失函数，如下所示：

${{\rm O}}_{\text{DeepSemi-NMF}}={\Vert X-P_1{P}_2\cdots P_l{Q}_l\Vert }_F^2$ (2)

矩阵P的更新规则，当优化第i层的矩阵P_i时，我们固定其他的矩阵。我们设置 $\frac{\partial {{\rm O}}_{\text{DeepSemi-NMF}}}{P_i}=0$ ，能够得到：

$P_i={\varphi }^{†}X{Q}_i^{†}$ (3)

其中 $\varphi =P_1{P}_2.\cdots P_{i-1}$ ， $†$ 是Moore-Penrose伪逆。

更新Q_i的规则与论文提到的更新过程相似 [12] ，我们能够得到下面的式子：

$Q_i\leftarrow Q\odot \sqrt{\frac{{\left[{\phi }^{\text{T}}X\right]}^{+}+{\left[{\phi }^{\text{T}}\phi \right]}^{-}{Q}_i}{{\left[{\phi }^{\text{T}}X\right]}^{-}+{\left[{\phi }^{\text{T}}\phi \right]}^{+}{Q}_i}}$ (4)

其中 ${\left[A\right]}^{+}=\frac{\left|A\right|+A}{2}$ ， ${\left[A\right]}^{-}=\frac{\left|A\right|-A}{2}$ ， $\phi =P_1{P}_2\cdots P_i$ 。

3. 提出方法

在本节我们会具体介绍我们的方法。

数学模型

深度半非负矩阵分解相较于单层的矩阵分解，能够更好地学习数据的隐藏信息，进而获得更好的聚类结果。但是我们发现现有的基于深度矩阵分解的多视图聚类算法，每一层的分解跟传统的矩阵分解类似，都忽略了重构残差。即在数据重构的时候，相似的数据点可能会分配到不相似的重构残差，这不利于学习每个视图的独特的特征。我们利用图嵌入的方法，在每一层的数据重构过程中，令每一层学习到Q和重构残差与原始数据能够保持相似结构。确保相似的数据点能够分配到相似的重构残差，更好的学习每个视图都有的特征。在视图融合策略上，我们利用自适应的方式让不同视图学习到的潜在空间相加，这样对于视图的重要性我们可以做到一个区分，重要视图占的比重更大，而不是所以视图都是在同一重要性，这有利于学到更好的潜在表达，提升算法灵活性。我们希望这些矩阵能够寻找到一个准确的共享潜在空间，根据论文提到 [13] ，基于对矩阵的广义低阶逼近，我们选择了一个宽松的谱嵌入结果FR，并将其用于潜在特征表示。这样，我们就可以使跨视角约束更加灵活，并获得更广阔的低维空间。当我们给定一个 $X=\left\{X^1,X^2,\cdots ,X^H\right\}$ 具有H个视图的多视图数据， $X^{\left(v\right)}\in {\Re }^{m_v\times n}$ ，我们提出的局部残差保持的深度矩阵算法(LRPDMF)的目标函数为：

$\begin{array}{l}\underset{P_k^{\left(v\right)},Q_k^{\left(v\right)},F,R,{\alpha }^{\left(v\right)}}{\min }{\displaystyle \underset{v=1}{\overset{H}{\sum }}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*i}^{\left(v\right)}-P_1^{\left(v\right)}{P}_2^{\left(v\right)}\cdots P_l^{\left(v\right)}{\left(Q_l\right)}_{*j}^{\left(v\right)}\Vert }_2^2{W}_{ij}^{\left(v\right)}}}}+\Vert {\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(H_l^{\left(v\right)}\right)}^{\text{T}}{H}_l^{\left(v\right)}}-F{R}^{\text{T}}\Vert \\ \text{s}\text{.t}.Q_k^{\left(v\right)}\ge 0,F^{\text{T}}F=I,{\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}=1},{\alpha }^{\left(v\right)}\ge 0.\end{array}$ (5)

其中， $X_{*i}^{\left(v\right)}$ 表示 $X^{\left(v\right)}$ 的第i列， ${\left(Q_l\right)}_{*j}^{\left(v\right)}$ 表示 $Q_l^{\left(v\right)}$ 的第j列。我们构造了一个0-1加权图 $W^{\left(v\right)}$ 来表示最近邻关系：

$W_{ij}^{\left(v\right)}=\{\begin{array}{l}1,\text{if}{X}_{*i}^{\left(v\right)}\in {\varphi }_q\left(X_{*j}^{\left(v\right)}\right)\text{or}{X}_{*j}^{\left(v\right)}\in {\varphi }_q\left(X_{*i}^{\left(v\right)}\right)\\ 0,\text{otherwise}\end{array}$ (6)

其中，其中 ${\varphi }_q\left(X_{*i}^{\left(v\right)}\right)$ 表示示例 $X_{*i}^{\left(v\right)}$ 的最近邻居的集合。

4. 算法优化

为实现目标函数，我们使用迭代优化的策略更新参数。

4.1. 关于 $P_k^{\left(v\right)}$ 的子问题

当 $Q_k^{\left(v\right)}$ ，F，R， ${\alpha }^{\left(v\right)}$ 被固定时，每一个 $P_k^{\left(v\right)}$ 是相互独立的，且任意一个视图的 $P_k$ 也是相互独立的，因此我们以任意视图为例，关于 $P_k$ 的优化式子可以写成：

$C={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*j}-\varphi P_k{\left(Q_k\right)}_{*i}\Vert }_2^2{W}_{ij}}}$ (7)

其中 $\varphi =P_1,P_2,\cdots ,P_{k-1}$ 。

特别的，公式(7)可以进一步写成：

$\begin{array}{c}C={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*j}-\varphi P_k{\left(Q_k\right)}_{*i}\Vert }_2^2{W}_{ij}}}\\ =tr\left(XD{X}^{\text{T}}-2XW{Q}_k^{\text{T}}{P}_k^{\text{T}}{\varphi }^{\text{T}}+\varphi P_k{Q}_{k}D{Q}_k^{\text{T}}{P}_k^{\text{T}}{\varphi }^{\text{T}}\right)\end{array}$ (8)

其中W的行(或列)和是对角矩阵D的元素，即 $D_{ii}={\displaystyle \underset{j}{\sum }{W}_{ij}}$ 。

目标函数(8)对P_k求偏导数，有：

$\frac{\partial C}{\partial P_k}=-{\varphi }^{T}XW{\left(Q_k\right)}^T+{\varphi }^T\varphi P_k{Q}_{k}D{Q}_k^T$ (9)

我们设置 $\frac{\partial C}{\partial P_k}=0$ ，很容易得到：

$P_k={\left({\varphi }^{\text{T}}\varphi \right)}^{-1}{\varphi }^{\text{T}}XW{Q}_k^{\text{T}}{\left(Q_{k}D{Q}_k^{\text{T}}\right)}^{-1}$ (10)

4.2. 关于 $Q_k^{\left(v\right)}$ 的子问题

当 $P_k^{\left(v\right)}$ ，F，R，α^(v)被固定时，且 $k<l$ ， $Q_k^{\left(v\right)}$ 是相互独立的，且任意一个视图的Q_k也是相互独立的，因此我们以任意视图为例，关于Q_k的优化式子可以写成：

$C={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*i}-\phi Q_{*J}\Vert }_2^2{W}_{ij}}}$ (11)

其中 $\phi =P_1{P}_2\cdots P_k$ 。

特别地，公式(11)可以被进一步写成：

$\begin{array}{c}C={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*i}-\phi Q_{*J}\Vert }_2^2{W}_{ij}}}\\ =tr\left(XD{X}^{\text{T}}-2XW{Q}_k^{\text{T}}{\phi }^{\text{T}}+\phi Q_{k}D{Q}_k^{\text{T}}{\phi }^{\text{T}}\right)\end{array}$ (12)

根据论文，我们可以得到Q_k k < l的更新规则为：

$Q_k=Q_k\odot \sqrt{\frac{{\left[{\phi }^{T}X\right]}^{+}W+{\left[{\phi }^T\phi \right]}^{-}{Q}_{k}D}{{\left[{\phi }^{T}X\right]}^{-}W+{\left[{\phi }^T\phi \right]}^{+}{Q}_{k}D}}$ (13)

当k = l时， $P_k^{\left(v\right)}$ ，F，R，α^(v)被固定时。关于 $Q_l^{\left(v\right)}$ 的优化式子可以写成：

$\begin{array}{c}C={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\Vert X_{*i}^{\left(v\right)}-\phi {\left(Q_l\right)}_{*j}^{\left(v\right)}\Vert }_2^2{W}_{ij}^{\left(v\right)}}}+{\Vert {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{Q}_l^{\left(v\right)}+G-F{R}^T\Vert }_F^2\\ =tr\left(X^{\left(v\right)}{D}^{\left(v\right)}{X}^{\left(v\right)}{}^{\text{T}}-2X^{\left(v\right)}{W}^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{\phi }^{\text{T}}+\phi Q_{{}_l}^{\left(v\right)}{D}^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{\phi }^{\text{T}}\right)\\ +\beta {\Vert {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{Q}_l^{\left(v\right)}+G-F{R}^{\text{T}}\Vert }_F^2\end{array}$ (14)

其中 $\phi =P_1{P}_2\cdots P_l$ ， $G={\displaystyle {\sum }_{o=1.o\ne v}^H{\alpha }^{\left(o\right)}{\left(Q_l^{\left(o\right)}\right)}^{\text{T}}{Q}_l^{\left(o\right)}}$ 。

公式(14)可以进一步转换成拉格朗日函数：

$\begin{array}{c}L\left(Q_l^{\left(v\right)}\right)=tr\left(X^{\left(v\right)}{D}^{\left(v\right)}{X}^{\left(v\right)}{}^{\text{T}}-2X^{\left(v\right)}{W}^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{\phi }^{\text{T}}+\phi Q_{{}_l}^{\left(v\right)}{D}^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{\phi }^{\text{T}}\right)\\ +\beta {\Vert {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{Q}_l^{\left(v\right)}+G-F{R}^T\Vert }_F^2-tr\left(\eta Q_l^{\left(v\right)}\right)\end{array}$ (15)

我们设置 $\frac{\partial L}{\partial Q_l^{\left(v\right)}}=0$ 。

$\begin{array}{c}\frac{\partial L}{\partial Q_l^{\left(v\right)}}=2({\phi }^{\text{T}}\phi Q_l^{\left(v\right)}{D}^{\left(v\right)}-{\phi }^{\text{T}}{X}^{\left(v\right)}{W}^{\left(v\right)}-2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}R{F}^{\text{T}}\\ +2\beta {\left({\alpha }^{\left(v\right)}\right)}^2{Q}_l^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}G)-\eta \\ =0\end{array}$ (16)

从互补松弛条件，我们可以得到：

$\begin{array}{l}({\phi }^{\text{T}}\phi Q_l^{\left(v\right)}{D}^{\left(v\right)}-{\phi }^{\text{T}}{X}^{\left(v\right)}{W}^{\left(v\right)}-2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}R{F}^{\text{T}}+2\beta {\left({\alpha }^{\left(v\right)}\right)}^2{Q}_l^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}\\ +2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}G)Q_l^{\left(v\right)}=\eta Q_l^{\left(v\right)}=0\end{array}$ (17)

我们把两边都乘以 $Q_l^{\left(v\right)}$ ，我们可以得到：

$\begin{array}{l}({\phi }^{\text{T}}\phi Q_l^{\left(v\right)}{D}^{\left(v\right)}-{\phi }^{\text{T}}{X}^{\left(v\right)}{W}^{\left(v\right)}-2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}R{F}^{\text{T}}+2\beta {\left({\alpha }^{\left(v\right)}\right)}^2{Q}_l^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}\\ +2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}G){\left(Q_l^{\left(v\right)}\right)}^2=0\end{array}$ (18)

公式(18)是一个不动点方程，我们可以得到 $Q_l^{\left(v\right)}$ 的更新规则为：

$Q_l^{\left(v\right)}=Q_l^{\left(v\right)}\odot \sqrt{\frac{ZHS}{ZHV}}$ (19)

其中 $ZHS={\left[{\phi }^{\text{T}}{X}^{\left(v\right)}\right]}^{+}{W}^{\left(v\right)}+{\left[{\phi }^{\text{T}}\phi \right]}^{-}{Q}_l^{\left(v\right)}{D}^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{\left[R{F}^{\text{T}}\right]}^{+}$ ，

$\begin{array}{c}ZHV={\left[{\phi }^{\text{T}}{X}^{\left(v\right)}\right]}^{-}{W}^{\left(v\right)}+{\left[{\phi }^{\text{T}}\phi \right]}^{\text{+}}{Q}_l^{\left(v\right)}{D}^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{\left[R{F}^{\text{T}}\right]}^{-}\\ +2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}+2\beta {\alpha }^{\left(v\right)}{Q}_l^{\left(v\right)}G\end{array}$

4.3. 关于R的子问题

当 $Q_k^{\left(v\right)}$ ， $P_k^{\left(v\right)}$ ，F，α^(v)被固定时，R的优化问题可以被写成：

$\underset{R}{\min }\beta {\Vert {\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}-F{R}^{\text{T}}}\Vert }_F^2$ (20)

根据正交约束 $F^{\text{T}}F=I$ ，我们可以得到公式(20)的解析解如下：

$R={\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}F}$ (21)

4.4. 关于F的子问题

当 $Q_k^{\left(v\right)}$ ， $P_k^{\left(v\right)}$ ，R，α^(v)被固定时，F的优化问题可以被写成：

$\underset{\text{s}\text{.t}.F^{\text{T}}F=I}{\min }\beta {\Vert {\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}-F{R}^{\text{T}}}\Vert }_F^2$ (22)

根据正交约束，公式(22)可以等价为：

$\underset{F^{\text{T}}F}{\max }\left(F{\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}R}\right)$ (23)

公式(23)是正交Procrustes问题，我们根据Fang等人 [14] 提出的求解方法。我们可以得到变量F的解析解：如果 $SVD=\left({\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}}{Q}_l^{\left(v\right)}R\right)=US{V}^{\text{T}}$ ，那么F = UV^T。

4.5. 关于α的子问题

当 $Q_k^{\left(v\right)}$ ， $P_k^{\left(v\right)}$ ，F，R被固定时，α的优化问题可以被写成：

$\begin{array}{l}\underset{\alpha }{\min }{\Vert {\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}-F{R}^{\text{T}}}\Vert }_F^2\\ \text{s}\text{.t}.{\displaystyle \underset{v=1}{\overset{H}{\sum }}{\alpha }^{\left(v\right)}}=1,{\alpha }^{\left(v\right)}>0\end{array}$ (24)

令 $S={\displaystyle \underset{v=1}{\overset{H}{\sum }}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}}$ ，Z = FR^T。我们有：

${\Vert S-Z\Vert }_F^2=tr\left(S^{\text{T}}S\right)-tr\left(2S{Z}^{\text{T}}\right)$ (25)

因为 $S={\displaystyle \underset{v=1}{\overset{H}{\sum }}{\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}}$ ，所以S = S^T，从而公式(25)可以被写成：

$\begin{array}{l}\underset{\alpha }{\min }\frac{1}{2}{\alpha }^{\text{T}}A\alpha -f^{\text{T}}\alpha \\ \text{s}\text{.t}.\alpha \ge 0\end{array}$ (26)

其中上述提到的变量定义如下：

$\begin{array}{l}{f}^{\text{T}}=\left[f_1,f_2,\cdots ,f_H\right],\\ f_v=tr\left({\left(Q_l^{\left(v\right)}\right)}^{\text{T}}{Q}_l^{\left(v\right)}R{F}^{\text{T}}\right),\\ A_{pq}=tr\left({\left(Q_l^{\left(p\right)}\right)}^{\text{T}}{Q}_l^{\left(p\right)}{\left(Q_l^{\left(q\right)}\right)}^{\text{T}}{Q}_l^{\left(q\right)}\right),\\ \alpha =\left[{\alpha }^{\left(1\right)},{\alpha }^{\left(2\right)},\cdots ,{\alpha }^{\left(H\right)}\right].\end{array}$ (27)

根据二次规划，公式(26)可以被求解。

5. 实验评估与分析

5.1. 实验设置

实验中我们用到三个数据集，我们对这三个数据集进行了简明扼要的描述。表1汇总了这些数据集的统计数据。本次实验，我们与当前最先进的方法进行比较，分别为MultiNMF [1] ，LPDiNMF [15] ，NMFCC [8] ，DMF-MVC [10] ，MvDGNMF [11] 。为了评估模型的性能，本文采用了三个评估指标：准确率(ACC) [16] 、归一化信息(NMI) [16] 和纯度(Purity) [17] 。这些指标值越高，说明算法性能越好。为了进行严格和公正的比较，每种方法都重复10次，以减少初始误差的影响。我们记录了结果的平均值和标准偏差。所有方法我们都根据原始出版物中的参数进行配置。

Table 1. Statistics of the datasets

表1. 数据集统计

5.2. 聚类算法对比结果

表2、表3、表4、展示了我们的算法与其他多视图算法在三个真实数据集上的聚类性能比较。我们提出的算法在三个数据中都取得了最好的结果。根据这些表格，我们可以得出以下结论：与MultiNMF、LPDiNMF、NMFCC基于矩阵分解方法相比，我们的方法取得了更好的聚类结果。相比于单层的矩阵分解，深度矩阵分解能够更好地挖掘数据的潜在信息，不同层次的信息能够被更好地表达。这种能力使我们处于优势地位，获得了更好的聚类结果。与深度矩阵分解方法(如DMF-MVC、MvDGNMF)相比，我们的方法在所有数据集上都取得了更好的结果，虽然我们的方法都是基于深度矩阵分解的方法，但是他们都忽略了每一层的重构残差，从而每一个视图的独有特征没有很好地被学习到，而我们提出的局部残差保持，在每一层的分解中都确保相似的重构残差能够分配到相似的数据点，每个视图的独有特征能更好地学习到，所以我们的方法取得了最好的聚类结果。所以，我们提出的算法是有效的。

Table 2. Clustering performance on BBCSport (%)

表2. 在BBCSport数据集上的聚类结果

Table 3. Clustering performance on BBC (%)

表3. 在BBC数据集上的聚类结果

Table 4. Clustering performance on HW (%)

表4. 在HW数据集上的聚类结果

5.3. 收敛分析

为了验证算法的收敛特性，我们在三个不同的数据集上进行了测试，迭代曲线如图1，图2，图3所示。随着迭代次数的增加，目标函数值逐渐趋于平稳，最终实现收敛。这证明了我们所采用的迭代优化方法的有效性。

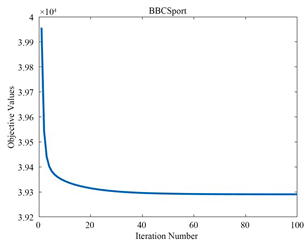
Figure 1. The objective function values of LRPDMF the versus number of iterations

图1. LRPDMF的目标函数值与迭代次数的关系

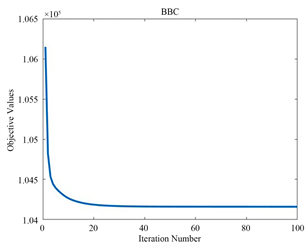
Figure 2. The objective function values of LRPDMF the versus number of iterations

图2. LRPDMF的目标函数值与迭代次数的关系

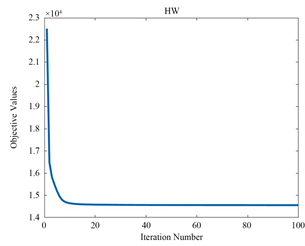
Figure 3. The objective function values of LRPDMF the versus number of iterations

图3. LRPDMF的目标函数值与迭代次数的关系

6. 总结

本文提出了一种局部残差保持的深度矩阵分解的多视图聚类算法，一方面，我们在每一层的分解都对局部残差进行了保持，所以我们能够更好地学习到每个视图的独有特征。另一方面，我们用自适应的方法来衡量不同视图的重要性，使其过滤掉一些无关信息，寻找到一个更加准确的潜在空间。在三个数据集上的实验证明了我们的算法是有效的。