1. 引言
如果一个FIR滤波器的脉冲响应函数具有对称性或反对称性,则其相位响应是频率的线性函数(或附加一个固定的初始相位),这样的滤波器称为线性相位FIR滤波器。由于系数的对称性,实现线性相位FIR滤波器所需要的乘法器数量只有相同长度FIR滤波器的(约)一半,并且没有相位失真,因而线性相位FIR滤波器在无线通信,图像处理,语音处理等领域有非常广泛的应用。在设计线性相位FIR滤波器时,通常需要给出通带和阻带的区间以及相应误差范围(如通带起伏,阻带衰减等),有时还需要附加一些时域或频域约束。常见的设计方法有窗函数法,频率采样法,等波纹法 [1] ,线性规划法,最小二乘法 [2] 等。这些方法在计算量,优化的目标函数,数值稳定性等方面差别较大。窗函数法最为简单,但它在任何意义上都不是最优的。在给定通带和阻带起伏的约束下,等波纹法可以得到最短的滤波器。它的通带和阻带具有等波纹特性,在最大误差最小化意义上是最优的。但这种方法无法兼容滤波器的时域和频域约束。线性规划法需要占用大量的内存空间并且计算时间较长。最小二乘法可以极小化误差的能量,但这种方法需要矩阵求逆运算,因而计算量较大。此外,该方法还存在数值稳定性问题,特别是在设计长滤波器时该问题更为突出。Vaidyanathan和Nguyen将线性相位FIR滤波器的设计表示成一个实对称正定矩阵的特征向量问题 [3] ,通过求解该矩阵的最小特征值所对应的特征向量即可得到滤波器的脉冲响应函数。随后该方法被推广至任意FIR滤波器的设计 [4] ,高阶数字差分器的设计 [5] ,IIR滤波器的设计 [6] ,2维FIR滤波器的设计 [7] 。该方法避免了复杂的矩阵求逆运算,可以用高效的迭代法仅仅求解一个特征向量。这个方法的另一个优点是可以兼容滤波器的时域和频域约束。但是该方法将零频设为参考频率,引入了不必要的附加约束。本文通过在通带取平均的方法,避免了参考频率的设定问题,并提高了线性相位FIR滤波器的设计性能。
2. 传统最小二乘法
一个因果的长度为N的FIR滤波器可以表示为
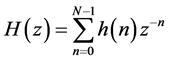 (1)
(1)
如果该滤波器的脉冲响应函数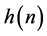 具有对称性,即
具有对称性,即 ,则其频率响应具有线性相位。如果N是偶数,该滤波器称为1型滤波器;如果N是奇数,该滤波器称为2型滤波器。其频率响应可表示为
,则其频率响应具有线性相位。如果N是偶数,该滤波器称为1型滤波器;如果N是奇数,该滤波器称为2型滤波器。其频率响应可表示为
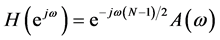 (2)
(2)
其中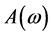 是幅度响应(实数)。
是幅度响应(实数)。
由于对称性,大约一半的滤波器系数不是独立未知数。N为奇数时,定义
 (3)
(3)
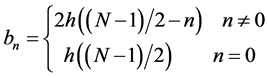 (4)
(4)
 (5)
(5)
 (6)
(6)
其中上标“T”代表转置。类似地,N为偶数时,定义
 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
则滤波器的幅度响应可表示为
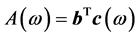 (11)
(11)
所谓滤波器设计就是求解未知的系数向量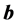 ,使其幅度响应尽可能逼近期望的幅度响应
,使其幅度响应尽可能逼近期望的幅度响应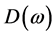 。
。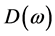 通常在通带为1而在阻带为0。设
通常在通带为1而在阻带为0。设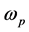 是通带截止频率,
是通带截止频率,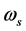 是阻带截止频率,R是通带和阻带的并集。传统最小二乘法就是极小化通带和阻带的均方误差
是阻带截止频率,R是通带和阻带的并集。传统最小二乘法就是极小化通带和阻带的均方误差
 (12)
(12)
其中矩阵 ,向量
,向量 ,标量d满足
,标量d满足
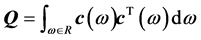 (13)
(13)
 (14)
(14)
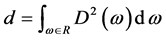 (15)
(15)
(12)中的目标函数是二次函数,对其求导并令导数为零可得
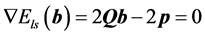 (16)
(16)
因此最优解为
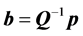 (17)
(17)
显然该方法包含矩阵求逆运算,计算量较大。
3. 传统特征滤波器法
阻带的均方误差可表示为
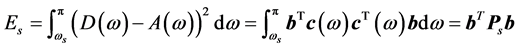 (18)
(18)
其中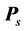 是一个实对称的正定矩阵
是一个实对称的正定矩阵
 (19)
(19)
与阻带不同,在通带难以将均方误差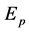 表示成系数向量
表示成系数向量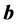 的二次函数。为此,引入零频处的频率响应
的二次函数。为此,引入零频处的频率响应 代替期望的频率响应
代替期望的频率响应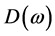 ,其中
,其中 是一个全是1的列向量。则有
是一个全是1的列向量。则有
 (20)
(20)
其中
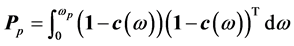 (21)
(21)
为了使通带和阻带的均方误差都极小化,可以极小化如下的凸组合:
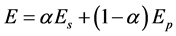 (22)
(22)
其中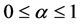 是在通带性能和阻带性能之间折衷的权系数。因此,最终的均方误差可以表示为
是在通带性能和阻带性能之间折衷的权系数。因此,最终的均方误差可以表示为
 (23)
(23)
其中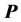 是一个实对称的正定矩阵。根据瑞利原理,在单位范数
是一个实对称的正定矩阵。根据瑞利原理,在单位范数 的约束下,极小化上述均方误差的最优解为矩阵
的约束下,极小化上述均方误差的最优解为矩阵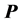 的最小特征值所对应的特征向量。由于仅计算一个特征向量,因而相对于矩阵求逆,该方法的计算量较小。
的最小特征值所对应的特征向量。由于仅计算一个特征向量,因而相对于矩阵求逆,该方法的计算量较小。
4. 改进的特征滤波器法
在传统的特征滤波器法中,选择零频处的幅度响应是为了引入滤波器的系数向量 。这相当于要求零频的幅度响应为通带响应的均值,因而施加了不必要的约束。这限制了滤波器在零频可能的幅度响应,例如不能为极值。因此,可以将通带内L个频率点的响应的均值
。这相当于要求零频的幅度响应为通带响应的均值,因而施加了不必要的约束。这限制了滤波器在零频可能的幅度响应,例如不能为极值。因此,可以将通带内L个频率点的响应的均值 作为期望响应,这样也可以引入滤波器的系数向量
作为期望响应,这样也可以引入滤波器的系数向量 。
。
 (24)
(24)
其中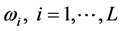 ,是通带内的离散频率点,
,是通带内的离散频率点,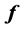 是这些频点上的平均响应
是这些频点上的平均响应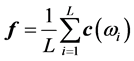 。因而通带的均方误差可表示为
。因而通带的均方误差可表示为
 (25)
(25)
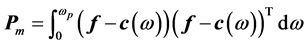 (26)
(26)
用 代替传统特征滤波器法中的
代替传统特征滤波器法中的 即为改进的特征滤波器法,即
即为改进的特征滤波器法,即
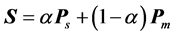 (27)
(27)
矩阵 的最小特征值所对应的特征向量即为滤波器的系数向量
的最小特征值所对应的特征向量即为滤波器的系数向量 ,再由(4)或(8)得到滤波器的脉冲响应函数。显然,该方法不需要人为指定一个参考频率。
,再由(4)或(8)得到滤波器的脉冲响应函数。显然,该方法不需要人为指定一个参考频率。
5. 设计举例
假定设计一个长度为149的低通线性相位滤波器,通带截止频率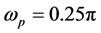 ,阻带截止频率
,阻带截止频率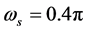 。利用Matlab平台用上述三个方法设计该滤波器。传统最小二乘法通过公式(17)的矩阵求逆实现,传统特征滤波器法通过求解矩阵
。利用Matlab平台用上述三个方法设计该滤波器。传统最小二乘法通过公式(17)的矩阵求逆实现,传统特征滤波器法通过求解矩阵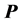 的最小特征值所对应的特征向量实现,改进的特征滤波器法通过求解矩阵
的最小特征值所对应的特征向量实现,改进的特征滤波器法通过求解矩阵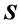 的最小特征值所对应的特征向量实现。用三个方法所设计的滤波器如图1所示。通过对比可见,传统最小二乘法具有(相对)最大的阻带旁瓣,传统特征滤波器法比传统最小二乘法具有较小的阻带旁瓣,而改进的特征滤波器法具有最小的阻带旁瓣。
的最小特征值所对应的特征向量实现。用三个方法所设计的滤波器如图1所示。通过对比可见,传统最小二乘法具有(相对)最大的阻带旁瓣,传统特征滤波器法比传统最小二乘法具有较小的阻带旁瓣,而改进的特征滤波器法具有最小的阻带旁瓣。
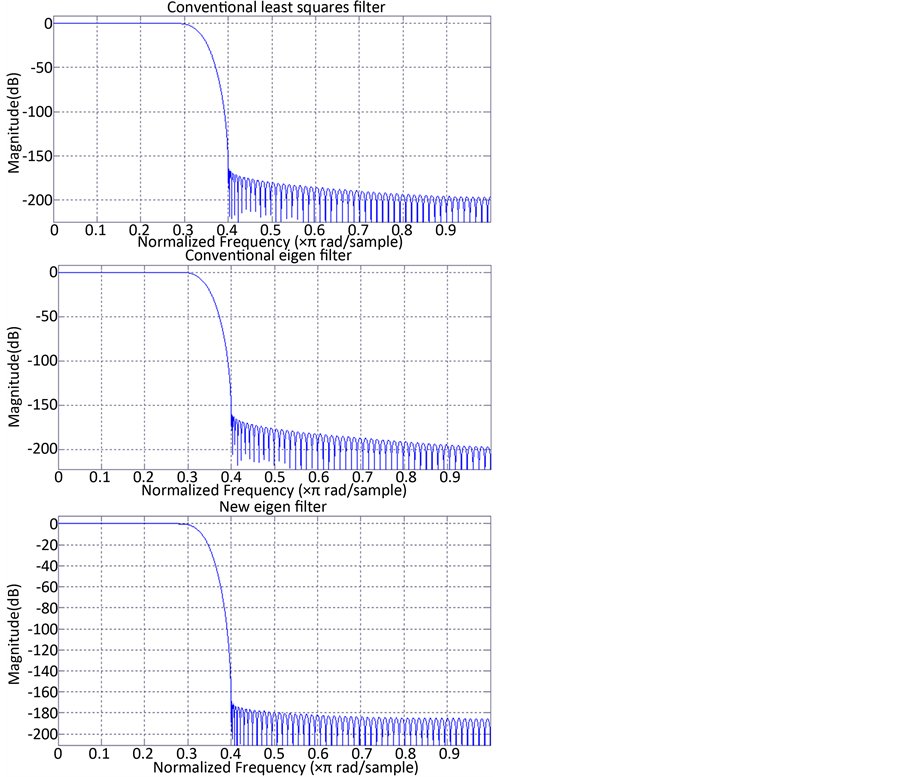
Figure 1. Frequency responses of low pass filters designed by the three methods (N = 149, ωp = 0.25 π, ωs = 0.4 π)
图1. 三种方法设计的低通滤波器(N = 149, ωp = 0.25 π, ωs = 0.4 π)
6. 结论
本文在分析比较了设计线性相位滤波器的传统最小二乘法和传统特征滤波器法的基础上,给出了一种改进的特征滤波器法。该方法通过在通带取平均的方法,避免了人为指定参考频率,可以获得更好的阻带衰减特性。