摘要:
本文基于Lyapunov-Krasovskii稳定性理论,线性矩阵不等式及自由权矩阵方法,设计了基于自适应数据的时滞混沌系统Lur’e系统的分数同步,提出了一种新的时滞相关指数同步判据,并设计了相应的自适应数据控制器。经Matlab仿真验证设计的控制器使得误差系统以较快的速度到达平衡点。本文研究的基于自适应时滞混沌Lur’e系统的保密通信研究可拓展应用到时滞Chua电路等,具有推广性。
Abstract:
Based on the Lyapunov-Krasovskii stability theory, linear matrix inequality and free weight matrix method, the fractional synchronization of Lur’e system with time-delay chaotic system based on adaptive data is designed. A new delay-dependent exponential synchronization criterion is proposed. And the corresponding adaptive data controller is designed. The controller designed by Matlab simulation verifies the error system to reach the equilibrium point at a faster speed. The research in secure communication, which is based on the adaptive time-delay chaotic Lur'e system, can be applied to the time-delay Chua circuit and can be extended to other fields.
1. 引言
混沌系统因其具有内随机性、连续宽谱及对初值极为敏感的特点在通信保密领域具有长远的应用前景 [1] 。随着研究任意阶次微积分算子的分数阶微积分的发展,分数阶混沌系统被提出和研究。分数阶系统具有更大的密钥空间,并且具有普遍性,使得分数阶混沌系统在通信保密领域具有更高的使用价值。一些分数阶混沌的方法如投影同步、耦合同步、主动控制同步、反馈控制同步、自适应控制同步等为其在保密通信领域的应用提供了理论基础。自Pecora和Carroll创造性提出的混沌系统的驱动——响应同步以来,混沌同步的理论价值在保密通信、信息处理等领域受到广泛的关注 [2] 。各种实现混沌同步的方法相继被提出,如混沌神经网络基于分散控制的驱动——响应同步,四维混沌系统基于自适应控制的改进投影同步,混沌系统基于可靠反馈控制的完全同步,混沌Lur’e系统基于时滞反馈控制的完全同步等 [3] 。
其中,Lur’e系统是一种典型的非线性系统,并且该系统的非线性项满足一个扇形有界的约束条件,Lur’e系统能够表述许多实际控制电路,如n-涡卷超混沌吸引子等 [4] 。Lur’e系统的方法有:利用常时滞输出反馈控制器给出两个相同的混沌Lur’e系统的完全同步,时滞混沌Lur’e系统的指数同步等。本文为了增加系统的可适用性,在改进的基础上研究一个分数阶带有采样数据时滞混沌Lur’e系统的混沌同步。
2. 时滞混沌Lur’e系统
2.1. 系统描述
考虑以下两个时滞混沌L’ure系统 [5] :
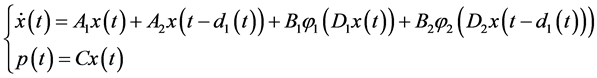 (1)
(1)
 (2)
(2)
其中, 和
和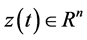 分别为驱动系统和响应系统的状态变量,
分别为驱动系统和响应系统的状态变量, 和
和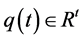 为系统的输出变量,
为系统的输出变量, 为控制输入,
为控制输入,
 和
和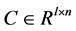 为已知常数的矩阵,
为已知常数的矩阵, 为时变时滞且满足
为时变时滞且满足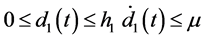 。
。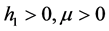 为常数。
为常数。
2.2. 系统特性
定义同步误差 则由驱动系统(1)和响应系统(2)可得误差系统为:
则由驱动系统(1)和响应系统(2)可得误差系统为:

其中,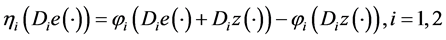
在文 [6]  ,
,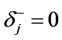 的基础上,引入下界
的基础上,引入下界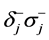 ,进行改进扇形条件,使其更具有普遍的推广性,使得
,进行改进扇形条件,使其更具有普遍的推广性,使得 ,
, 。
。
由此可得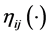 满足以下条件:
满足以下条件:
 (3)
(3)
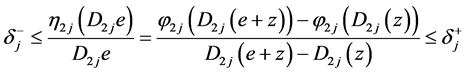 (4)
(4)
其中,如图1所示 ,
, ,
, 为
为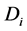 的第
的第 行向量。
行向量。
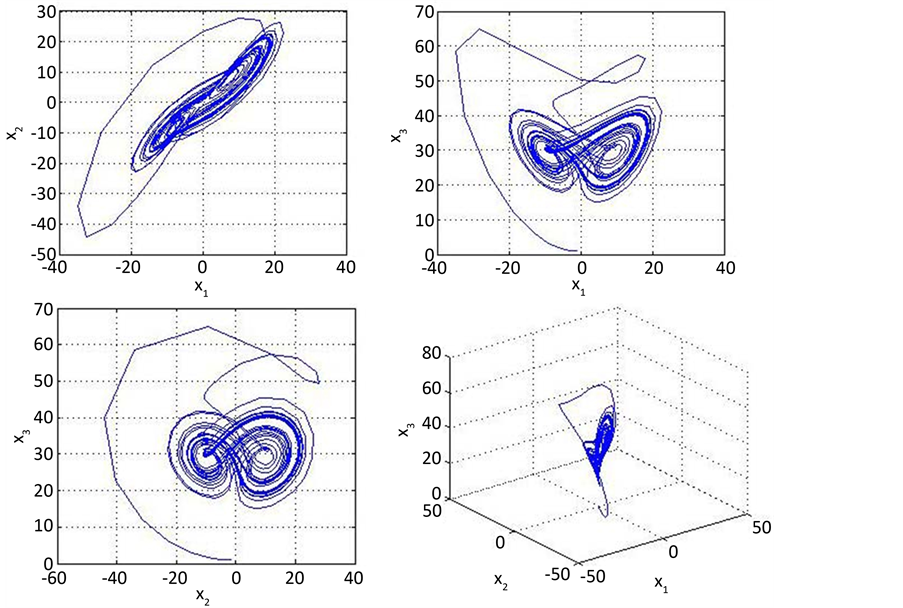
Figure 1. Attractor of the chaotic system of fractional order L’ure obtained by numerical simulation
图1. 数值模拟得到的分数阶L’ure混沌系统吸引子
2.3. 设计三维分数阶混沌误差系统
 (5)
(5)
 (6)
(6)
其中,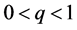 ,
,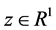 ,
,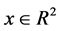 为误差系统的变量,
为误差系统的变量,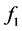 和
和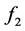 为非线性连续微分方程,且
为非线性连续微分方程,且 。
。
假设1:函数 在
在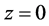 附近是平滑连续的,其子系统对于所有的渐近稳定于原点;
附近是平滑连续的,其子系统对于所有的渐近稳定于原点;
注1:本文研究的为分数阶时滞混沌L’ure系统,可以推广应用到其他一般系统;
注2:函数 在
在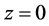 附近平滑连续,即存在
附近平滑连续,即存在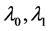 满足:
满足:
 (7)
(7)
 (8)
(8)
2.4. 自适应控制器
为了使误差系统稳定在平衡点 ,
,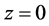 ,本文设计自适应控制器
,本文设计自适应控制器 ,使得
,使得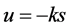
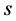 定义为:
定义为:
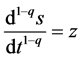 (9)
(9)
其中 为自适应律,
为自适应律,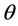 为任意正实数;
为任意正实数;
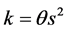 (10)
(10)
定理1:从任何初始值出发,误差系统(5) (6)在控制器(9)和自适应律(10)的作用下渐近稳定 [7] 。
考虑以下Lyapunov函数 [8] :
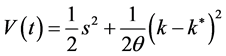 (11)
(11)
其中, 将上式求导可得:
将上式求导可得:
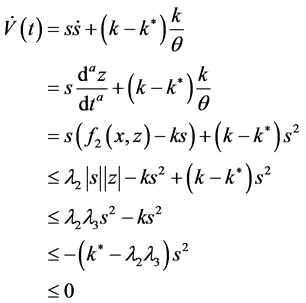 (12)
(12)
根据Barbalat定理 [9] ,随着时间的演化,可以得到随着 ,有
,有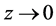 。并且根据假设1可知随着时间的演化
。并且根据假设1可知随着时间的演化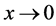 ,最终
,最终 ,
,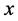 都逐渐趋近于0。
都逐渐趋近于0。
3. 数值仿真
通过数值仿真模拟 [10] 得到系统的误差同步图,如图2~图4所示。由图中可以看出,驱动系统与相
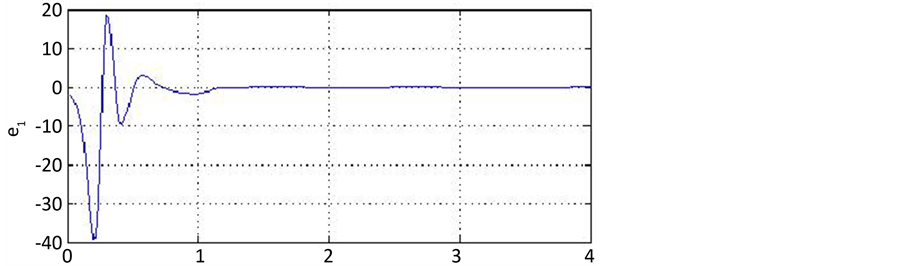
Figure 2. Synchronization error c1 evolution in chaotic systems of fractional order Lur’e
图2.分数阶Lur’e混沌系统同步误差c1演化图

Figure 3. Synchronization error c2 evolution in chaotic systems of fractional order Lur’e
图3.分数阶Lur’e混沌系统同步误差c2演化图

Figure 4. Synchronization error c3 evolution in chaotic systems of fractional order Lur’e
图4.分数阶Lur’e混沌系统同步误差c3演化图
应系统在较短时间内便趋近于同步。
在响应系统与驱动系统保持同步之后,利用响应系统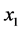 的变量对信号
的变量对信号 进行相加运算即掩盖加密 [11] ,加密后的信号成为
进行相加运算即掩盖加密 [11] ,加密后的信号成为 ,将此信号进行发送,驱动系统即接受者接收到此加密后的信号对其进行解密即
,将此信号进行发送,驱动系统即接受者接收到此加密后的信号对其进行解密即 我们已经知道驱动系统与响应系统在同步控制器的作用下保持了一致即
我们已经知道驱动系统与响应系统在同步控制器的作用下保持了一致即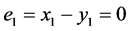 ,因此有
,因此有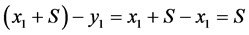 这样便能够把信息恢复出来。
这样便能够把信息恢复出来。
4. 结论
本文以时滞混沌Lur’e系统为例,研究其动态特性及其时滞系统的混沌特性,并提出了一种自适应非线性反馈控制器,实现了时滞混沌Lur’e系统的自时滞混沌同步。该控制器只包含当前的系统状态,不涉及时滞因数,且只对部分状态进行控制,原理简单,易于工程实现。自时滞同步使时滞系统和原系统同步,能够避免现实中因为时滞而产生的各种问题。它是自同步的扩展,进一步拓宽了研究同步问题的视野,具有非常重要的现实意义和理论价值。同时,时滞混沌系统应用在混沌保密通信中也可以更好地提高保密性能。
基金项目
河北省自然科学基金(项目编号F2016209382)双边遥操作多机器人系统时滞依赖协同控制研究;河北省唐山市华北理工大学大学生创新训练项目(X2016110)混沌同步在WSN通信加密的应用。