1. 引言
随着电子商务的快速发展,使得越来越多的制造商通过直销渠道直接向消费者销售产品。虽然许多制造商从事销售,但是研究商家在多渠道供应链下的竞争也越来越重要 [1] 。Chiang等 [2] 表明了制造商可以通过引入直销渠道来减轻利润损失。Kumar等 [3] 讨论了制造商在零售渠道的基础上直接开通直销渠道来获得更大的利润,同时零售商也将获益。
目前,在双渠道管理中的大量研究往往侧重于定价策略。Huang等 [4] 研究了当生产成本中断时,双通道供应链中的定价和生产问题。Jiang等 [5] 研究了供应链系统中的定价策略问题,其中制造商可以通过零售渠道和直销渠道销售原始产品和再制造产品。Dan等 [6] 利用两级优化技术和Stackelberg博弈考虑了双渠道供应链中的最优定价和零售服务。数值研究表明,零售渠道的顾客忠诚度和需求相对增长率在零售服务和定价策略上有很大的影响。在研究定价策略的基础上,人们也考虑了服务价值这个因素。Yao等 [7] 给出了一个带有服务价值的供应链,这是由一个制造商和两个零售商构成的。在一定条件下,他们证明了均衡价格和服务价值的存在性。Tsay等 [8] 讨论了一个制造商向两个独立零售商提供相同产品的供应链,并且研究了两个独立零售商在价格和服务策略上相互竞争。
多年来,寡头竞争博弈模型及其复杂性研究一直受到学者们的关注,所以系统动力学是一个重要的研究视角。Ma等 [9] 建立了一个Cournot-Bertrand混合双寡头博弈模型,并利用参数盆图分析了分岔和混沌等复杂动力学现象。Zhang等 [10] 考虑了双渠道供应链中两种不同的定价策略。通过数值模拟,他们分析了公平关系系数和决策参数对两个模型的复杂非线性动力学行为的影响。
受以上文献启发,本文考虑了由一个制造商和一个零售商组成的双渠道供应链的动态定价策略。我们研究了Nash均衡决策下的静态和动态博弈模型,分析了服务成本参数和渠道参数对系统的影响,并通过分岔图和最大Lyapunov指数图分析了该模型的动力学现象。
2. 问题描述与模型假设
本文研究了一个由单一制造商和单一零售商组成的考虑服务价值的双渠道供应链。模型有两个销售渠道:一个是制造商将产品以 的批发价批发给零售商,零售商再以
的批发价批发给零售商,零售商再以 的零售价销售给消费者的传统渠道;另一个是制造商直接将产品以
的零售价销售给消费者的传统渠道;另一个是制造商直接将产品以 的价格销售给消费者的直销渠道。模型如图1所示。
的价格销售给消费者的直销渠道。模型如图1所示。
和直销渠道相比,在传统渠道中,零售商会给消费者提供较好的服务 [8] ,s表示零售商通过传统渠道给消费者提供了一个服务价值。为了保证零售商是盈利的,假设 ,并且不失一般性,我们假设
,并且不失一般性,我们假设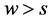 。本文可以使用一个严格凸的服务函数
。本文可以使用一个严格凸的服务函数 来描述服务价值及其相关成本之间的关系。服务成本函数
来描述服务价值及其相关成本之间的关系。服务成本函数

Figure 1. Dual-channel supply chain model
图1. 双渠道供应链模型
为 。表1中的参数都大于零。
。表1中的参数都大于零。
3. Nash均衡模型
3.1. 静态Nash均衡模型
在模型中,制造商和零售商具有平等的地位。制造商决策批发价 和直销价
和直销价 ,同时零售商决策零售价
,同时零售商决策零售价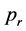 和服务价值
和服务价值 。假设零售商的边际利润为
。假设零售商的边际利润为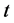 ,即
,即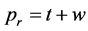 。两种渠道下的需求函数 [7] 分别为:
。两种渠道下的需求函数 [7] 分别为:
直销渠道需求:
 (1)
(1)
传统渠道需求:
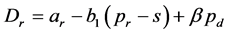 (2)
(2)
一般来说,参数应该满足以下条件:(i) ;(ii)
;(ii) 。即:
。即:
 (3)
(3)
 (4)
(4)
制造商的利润为
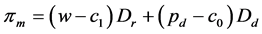 (5)
(5)
零售商的利润为
 (6)
(6)
供应链的总利润为
 (7)
(7)
 和
和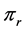 的Hessian矩阵分别是:
的Hessian矩阵分别是:
 和
和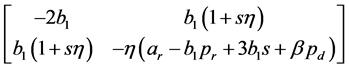 .
.
对于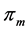 的Hessian矩阵来说,由于
的Hessian矩阵来说,由于 ,所以Hessian矩阵是负定的。此时,制造商的利润是凹的并且存在唯一的最优解。对于
,所以Hessian矩阵是负定的。此时,制造商的利润是凹的并且存在唯一的最优解。对于 的Hessian矩阵来说,由于
的Hessian矩阵来说,由于 ,当
,当
表1. 符号
满足 时,Hessian矩阵是负定的。此时,零售商的利润是凹的并且存在唯一的最优解。故Nash均衡存在最优解。
时,Hessian矩阵是负定的。此时,零售商的利润是凹的并且存在唯一的最优解。故Nash均衡存在最优解。
对 和
和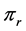 分别求关于
分别求关于 和
和 的一阶偏导数
的一阶偏导数
 (8)
(8)
由它们的一阶条件可得系统的最优解为:
 ,
,
 ,
,
 ,
,
 .
.
将 分别代入(5)、(6)和(7)式即可算出制造商利润、零售商利润和供应链的总利润。
分别代入(5)、(6)和(7)式即可算出制造商利润、零售商利润和供应链的总利润。
3.1.1. 服务成本参数对系统的影响
取参数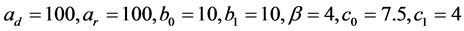 进行数值模拟。分析了服务成本参数对
进行数值模拟。分析了服务成本参数对 以及制造商利润、零售商利润和供应链总利润的影响。如图2所示。
以及制造商利润、零售商利润和供应链总利润的影响。如图2所示。
由图2可知:价格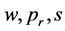 和利润
和利润 都随着服务成本参数
都随着服务成本参数 的增加而减小,直销价
的增加而减小,直销价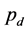 随着服务成本参数
随着服务成本参数 的增加而不变。所以在实际中,零售商应降低自己的服务成本参数来提高服务价值,从而利润也将得到提升。
的增加而不变。所以在实际中,零售商应降低自己的服务成本参数来提高服务价值,从而利润也将得到提升。
3.1.2. 渠道参数对系统的影响
取参数 进行数值模拟。分析了渠道参数对
进行数值模拟。分析了渠道参数对 以及制造商利润、零售商利润和供应链总利润的影响。如图3所示。
以及制造商利润、零售商利润和供应链总利润的影响。如图3所示。
由图3可知:价格 和利润
和利润 都随着渠道参数
都随着渠道参数 的增加而增加,服务价值
的增加而增加,服务价值 随着渠道参数
随着渠道参数 的增加而不变。结合实际情况,较大的渠道参数
的增加而不变。结合实际情况,较大的渠道参数 对制造商、零售商和系统供应链是有利的。
对制造商、零售商和系统供应链是有利的。
3.2. 动态Nash均衡模型
本节考虑了制造商和零售商分别对直销价、批发价和零售价、服务价值采取有限理性的决策 [11] [12] ,建立动态模型如下
 (9)
(9)
其中 是有限理性调整参数。
是有限理性调整参数。
3.2.1. 调整参数对系统的影响
下面利用数值模拟来研究系统(9)的动力学性质。根据实际情况与约束条件,取参数为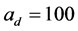 ,
,
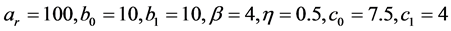 ,从而均衡点为
,从而均衡点为
 .
.
从图4可以看出,当 时,价格
时,价格 和利润
和利润 随
随 变化的分岔图及其最大Lyapunov指数图。当
变化的分岔图及其最大Lyapunov指数图。当 时,系统(9)处于稳定状态;当
时,系统(9)处于稳定状态;当 时,系统(9)处于倍周期状态;当
时,系统(9)处于倍周期状态;当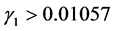 时,系统(9)处于混沌状态。过大的批发价调整速度会使系统(9)失去稳定性。很显然,开通直销渠道对制造商是有利的。
时,系统(9)处于混沌状态。过大的批发价调整速度会使系统(9)失去稳定性。很显然,开通直销渠道对制造商是有利的。
3.2.2. 服务成本参数对系统的影响
根据实际情况与约束条件,取参数为 。
。
表2给出了服务成本参数 在稳定域和分岔域内分别对制造商平均利润的影响。表3给出了服务成本参数
在稳定域和分岔域内分别对制造商平均利润的影响。表3给出了服务成本参数 在稳定和分岔域内分别对零售商平均利润的影响。表4给出了服务成本参数
在稳定和分岔域内分别对零售商平均利润的影响。表4给出了服务成本参数 在稳定和分岔域内分别对供应链系统平均利润的影响。从中可以看出:在稳定域和分岔域内,较小的服务成本参数
在稳定和分岔域内分别对供应链系统平均利润的影响。从中可以看出:在稳定域和分岔域内,较小的服务成本参数 对制造商、零售商和系统供应链是有利的。过大的服务成本参数
对制造商、零售商和系统供应链是有利的。过大的服务成本参数 会导致长期平均利润降低。
会导致长期平均利润降低。
图2. 对
对 和
和 的影响
的影响
图3.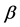 对
对 和
和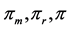 的影响
的影响
(c) 随
随 变化的分岔图
变化的分岔图
Figure 3. Bifurcation diagrams and the largest Lyapunov exponent plot of the system (9) for 
图4. 系统(9)随 变化的分岔图及其最大Lyapunov指数图
变化的分岔图及其最大Lyapunov指数图

Table 2. The average profit of the manufacturer for
表2. 制造商 的平均利润随
的平均利润随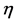 的变化
的变化

Table 3. The average profit of the retailer for
表3. 零售商 的平均利润随
的平均利润随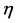 的变化
的变化

Table 4. The average profit of supply chain system for
表4. 供应链系统 的平均利润随
的平均利润随 的变化
的变化
4. 结论
本文考虑了由一个制造商和一个零售商组成的带有服务价值的双渠道供应链的动态定价策略。与以往研究不同的是,文本不仅研究了Nash均衡决策下的动态定价模型,而且还分析了在静态定价模型下服务成本参数和渠道参数对利润、定价和服务价值的影响。利用分岔图和最大Lyapunov指数图分析了分岔和混沌等复杂动力学现象。研究表明:在静态模型下,较大的渠道参数对制造商、零售商和系统供应链是有利的;在动态模型下,较大的调整参数会使系统失去稳定出现倍周期分岔,过大的服务成本参数会导致长期平均利润降低。所以零售商应降低自己的服务成本参数来提高服务价值,从而利润也将得到提升。对本文进一步的研究可以考虑产品的质量和旧产品的回收等问题。
NOTES
*通讯作者。