1. 引言
耕地地力也称耕地基础地力,是指在特定气候区域由地形、地貌、成土母质、土壤理化性状、农田基本建设及肥力培育水平等要素综合构成的耕地生产能力 [1] [2] 。耕地地力水平是影响作物生长发育的核心因素,直接决定着农产品产量和质量 [3] 。我国是一个耕地资源严重约束型国家,人均耕地面积远低于世界平均水平,且空间分布不均衡,基础地力偏低,中低产田比例较高。作为世界第一人口大国,我国粮食安全战略将持续面临巨大压力与挑战。河南省是传统的农业大省,是我国最重要的粮食主产区之一,在国家粮食安全战略中的地位与作用突出。为实现《国家粮食核心区建设规划》、《河南省高标准粮田“百千万”工程建设规划》提出的战略目标,河南省正坚持以耕地质量建设为核心,依靠科技进步,大力实施耕地质量培育措施,改善耕地土壤理化性状,提升耕地综合生产能力,强化抗御自然灾害的能力,保护农业生态环境。各项耕地质量培育、综合地力提升技术措施的有效实施,都离不开对耕地生产力现状的全面了解、系统评价以及对耕地地力等级的科学划分、对不同等级耕地资源空间分布格局的准确掌握。
在我国耕地地力评价与分级实践中,综合指数法是应用最为广泛的评价方法,也是我国农业行业标准(NY/T 1634-2008)中规定的耕地地力评价方法。这种方法是在确定评价因子及其权重和隶属度值的基础上,采用加法模型计算评价单元的综合地力指数,然后根据综合地力指数分布确定分级方案、划分地力等级 [4] 。尽管综合指数法在全国范围内、尤其是全国县域尺度耕地地力评价实践中具有基本一致的技术规程和实施方案,但步骤复杂,工作量大。在国内一些案例研究中,机器学习、决策分析等领域内的新技术、新方法被用于耕地地力评价,如粗糙集(Rough Set, RS)和支持向量机(SupportVector Machine, SVM)结合的组合算法 [5] [6] 、ID3 (Iterative Dichotomizer 3)、C4.5、模糊支持决策算法 [7] [8] [9] [10] 以及分类与回归树算法 [11] 等。
判别分析(Discriminant Analysis)是一种依据已知类别的样本在若干指标上的观察值,建立关于指标的判别函数或判别准则,并据此对新样本进行分类的多元统计分析方法。根据建立的判别准则不同,具体的判别分析方法可分为距离判别法、Fisher判别法、Bayes判别法以及逐步判别法等。广义上,判别分析是一种机器学习(Machine Learning)技术,自20世纪30年代问世以来,在自然科学、人文社科以及经济管理领域的应用日益广泛 [12] [13] 。其中,Bayes判别(Bayes Discriminant)是一种以Bayes法则(Bayes theorem)为核心的判别分析方法,它根植于18世纪英格兰著名数学家、长老会牧师Thomas Bayes的概率统计学思想,简述为:当无法准确知悉一个事物的本质时,可依靠与事物特定本质相关的事件出现的频率去判断其本质属性的概率;或换言之:支持某项属性的事件发生得愈多,则该属性成立的可能性就愈大。如果事件的结果不确定,那么量化它的唯一方法就是事件的发生概率;如果过去试验中事件的出现率已知,那么根据数学方法可以计算出未来试验中事件出现的概率,这就是Bayes判别分析的理论基础 [14] [15] [16] [17] 。Bayes判别分析在国内矿藏评估 [18] [19] 、风险预警 [20] [21] [22] 、财务分析 [23] [24] 、交通规划 [25] [26] 、疾病诊断 [27] [28] 、智能识别 [29] [30] [31] 等领域应用广泛,但在土壤质量和土地资源评价方面的应用较为少见。本文尝试将Bayes判别分析引入耕地地力评价实践中,探索一条区域尺度上耕地地力分类预测及中低产田划分的新途径。
2. 数据与方法
2.1. 数据来源
研究区辉县市地处河南省西北部,地理坐标北纬35˚17'~35˚50',东经113˚20'~113˚57'之间(图1),国土面积2007平方公里,境内西部为太行山脉,山地面积1007 km2,平原面积783 km2、丘陵217 km2,全市耕地面积5.34 × 104 km2。本研究的主要数据源为辉县市测土配方施肥补贴项目及其耕地地力评价专项(2010年~2012年)获取的耕地表层土壤属性数据、立地环境数据、第二次土地调查土地利用数据库、最新修订的土壤图、地形图等相关图件资料等。2012年辉县市依据农业部颁布的我国农业行业标准《耕地地力调查与质量评价技术规程(NY/T 1634-2008)》完成了全市耕地地力评价工作。实施过程中,以土壤图和土地利用现状图叠加产生的图斑作为耕地地力基本评价单元,选取表层土壤质地(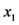 )、土壤剖面特征(
)、土壤剖面特征( )、地表砾石度(
)、地表砾石度(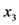 )、土壤速效钾(
)、土壤速效钾(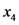 )、有效磷(
)、有效磷(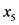 )、有机质含量(
)、有机质含量(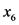 )、灌溉保证率(
)、灌溉保证率(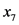 )、排涝能力(
)、排涝能力( )、地貌类型(
)、地貌类型( )以及地表坡度(
)以及地表坡度( )等10个对辉县市耕地生产性能影响较大、区域内空间变异明显、且在时间序列上具有相对稳定性、与农业生产关系密切的因素作为耕地地力评价指标 [32] ;利用层次分析法,建立评价指标与耕地潜在生产能力间的层次分析模型,计算单指标对耕地地力的权重;表层土壤质地、土壤剖面特征、灌溉保证率、排涝能力、地表砾石度、地貌类型等概念型因子赋值后,其隶属度采用专家打分法确定,土壤有机质含量、土壤有效磷、速效钾以及地表坡度等定量因子则采用特尔斐法根据实测值评估对应的隶属度。
)等10个对辉县市耕地生产性能影响较大、区域内空间变异明显、且在时间序列上具有相对稳定性、与农业生产关系密切的因素作为耕地地力评价指标 [32] ;利用层次分析法,建立评价指标与耕地潜在生产能力间的层次分析模型,计算单指标对耕地地力的权重;表层土壤质地、土壤剖面特征、灌溉保证率、排涝能力、地表砾石度、地貌类型等概念型因子赋值后,其隶属度采用专家打分法确定,土壤有机质含量、土壤有效磷、速效钾以及地表坡度等定量因子则采用特尔斐法根据实测值评估对应的隶属度。
2.2. 研究方法
2.2.1. Bayes判别函数
Bayes判别分析的一个基本假设是对所研究对象(总体)在抽样前已有一定认识,通常用先验概率来描述这种认识。Bayes判别就是根据总体的先验概率,使误判的平均损失达到最小而进行的判别。在本研究中,将研究区耕地评价单元分为k个不同耕地地力等级的总体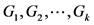 ,每个总体含p个与土壤理化性质和立地条件相关的评价指标,
,每个总体含p个与土壤理化性质和立地条件相关的评价指标,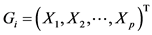 ,对应p维样本空间
,对应p维样本空间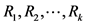 ,p元正态分布总体
,p元正态分布总体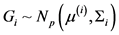 ,
, ,分布密度函数 [33] 为:
,分布密度函数 [33] 为:
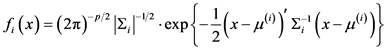 (1)
(1)
不同地力等级的耕地评价单元的先验概率分别为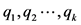 ,其取值由研究区内各等级耕地的面积比确定(表1):
,其取值由研究区内各等级耕地的面积比确定(表1):
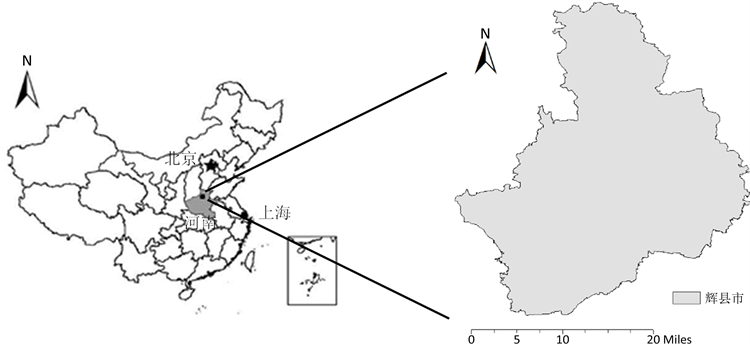
Figure 1. The map of the location of Huixian City
图1. 辉县市地理位置示意图

Table 1. Prior probability of the land evaluation units with different fertility classes
表1. 研究区不同地力等级耕地评价单元的先验概率
将地力等级为i的样本错判为地力等级j造成的损失为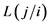 ,发生这种错判的概率为:
,发生这种错判的概率为:
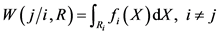 (2)
(2)
错判造成的总平均损失 [34] 为:
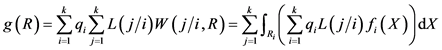 (3)
(3)
样品落入总体Gi对应的空间Ri的概率即后验概率为:
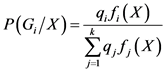 (4)
(4)
当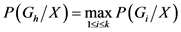 时,样本X被判入地力等级为h的总体Gh。Bayes判别分析的本质其实就是构造一个对p维空间的最优划分,使得后验概率最大,同时使错判造成的平均损失最小[35]。错判地力等级的损失可以给出定性的分析,但很难定量描述,故假定各错判损失均相同。如此,平均错判损失最小与后验概率最大相互等价,即使得
时,样本X被判入地力等级为h的总体Gh。Bayes判别分析的本质其实就是构造一个对p维空间的最优划分,使得后验概率最大,同时使错判造成的平均损失最小[35]。错判地力等级的损失可以给出定性的分析,但很难定量描述,故假定各错判损失均相同。如此,平均错判损失最小与后验概率最大相互等价,即使得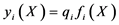 最大 [34] ,p元正态分布总体的概率函数见式(1)。
最大 [34] ,p元正态分布总体的概率函数见式(1)。
令 ,则判别函数 [33] [34] 为:
,则判别函数 [33] [34] 为:
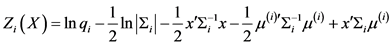 (5)
(5)
后验概率记为:
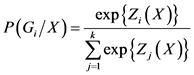 (6)
(6)
把未知地力等级的样本X代入判别式,分别计算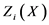 ,使
,使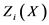 为最大的总体Gi,如后验概率
为最大的总体Gi,如后验概率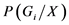 也最大,则把样品X归为总体Gi,耕地地力等级为i。
也最大,则把样品X归为总体Gi,耕地地力等级为i。
2.2.2. Bayes判别检验与修正
① 检验原假设H01: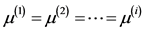
一般耕地地力共有多个等级,对于总体数量k > 2的情况通常分两步来检验,首先检验k个等级的耕地总体的评价指标均值向量是否全相等,构建维尔克斯统计量 [34] :
 (7)
(7)
Lxx为各总体组内离差阵之和: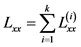 ,
,
B为组间离差阵: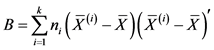 ,
,
构造统计量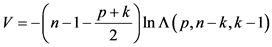 近似服从自由度为
近似服从自由度为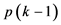 的
的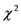 分布,根据p值大小判断是否拒绝原假设。若接受原假设,即各等级耕地的指标均值全部相等,说明这些耕地的土壤理化性状、立地条件、障碍因素等条件没有显著差异,耕地等级需进行合并;若不全相等,则进行下一步两两逐对检验。
分布,根据p值大小判断是否拒绝原假设。若接受原假设,即各等级耕地的指标均值全部相等,说明这些耕地的土壤理化性状、立地条件、障碍因素等条件没有显著差异,耕地等级需进行合并;若不全相等,则进行下一步两两逐对检验。
② 检验原假设H02: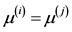
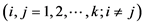
检验每两个总体之间差异的显著性,构造统计量 [34] 为:
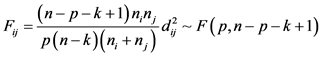 (8)
(8)
服从分子自由度为p,分母自由度为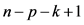 的F分布,
的F分布,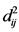 为两个总体间的马氏距离:
为两个总体间的马氏距离:
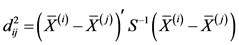
S−1为组间协方差阵的逆矩阵: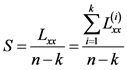
如结果接受原假设,则均值相等的两个地力等级的土壤理化性状、立地条件等因素差异不明显,应合并为一个总体,与其他均值向量不同的耕地总体重新构建判别函数;若拒绝原假设,说明两类地力等级已经得以最优划分,判别函数有效。
3. 结果与讨论
3.1. 判别函数的构建
按照《耕地地力调查与质量评价技术规程(NY/T 1634-2008)》,将研究区耕地评价单元分为4个地力等级的总体,每个总体由表层土壤质地(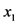 )、土壤剖面特征(
)、土壤剖面特征(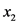 )、地表砾石度(
)、地表砾石度(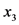 )、速效钾(
)、速效钾( )、有效磷(
)、有效磷( )、有机质含量(
)、有机质含量(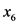 )、灌溉保证率(
)、灌溉保证率(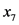 )、排涝能力(
)、排涝能力(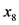 )、地貌类型(
)、地貌类型(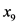 )、坡度(
)、坡度(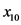 )等10个评价因子描述。其中,1、2、3、4地力等级总体的先验概率分别为0.35、0.34、0.25、0.06,基于研究区测土配方施肥项目耕地地力评价中使用的评价因子对耕地地力影响的权重及其对应隶属度数据,采用耕地自然要素评价指数来反映耕地潜在生产能力的高低,关系式为:
)等10个评价因子描述。其中,1、2、3、4地力等级总体的先验概率分别为0.35、0.34、0.25、0.06,基于研究区测土配方施肥项目耕地地力评价中使用的评价因子对耕地地力影响的权重及其对应隶属度数据,采用耕地自然要素评价指数来反映耕地潜在生产能力的高低,关系式为:
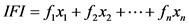 (9)
(9)
其中,IFI为耕地地力指数,fi为耕地自然属性分,xi为该评价因子的权重。假设各总体的协方差矩阵相等,且均为多元正态总体,根据各因子权重数据、原始数据及其隶属度求得耕地地力指数,利用统计分析工具SPSS判别分析模块,计算4个总体Bayes判别函数各项系数,结果列入表2。
将表2中的自变量系数和常数项代入4个耕地地力等级的Bayes判别函数,自变量为评价单元的耕地地力指数,获得其线性函数形式:
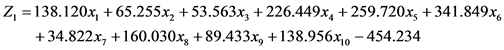
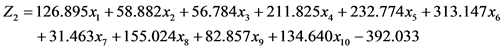
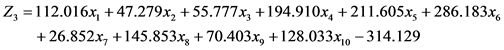

将未知地力等级评价单元的耕地地力指数分别代入4个地力等级的判别函数,当Zi最大时,样本落入对应等级的概率最大,从而将样本划入这一地力等级。基于研究区所有耕地评价单元的相关数据进行Bayes判别函数的回代检验,结果列入表3。
结果显示存在误判情况,原始资料中耕地地力等级为二等的评价单元在Bayes判别规则下有283个评价单元判为一等地,148个评价单元判为三等地;三等地评价单元有54个误判为二等地,23个误判为

Table 2. Coefficients of Bayes discriminant functions
表2. Bayes判别函数系数
四等地;四等地评价单元有139个误判为三等地。与测土配方施肥项目开展的辉县市耕地地力评价资料相比,误判率为10.9%。
3.2. 判别函数检验与分析
依照前文中的式(7)构造维尔克斯统计量,计算结果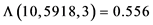 ,变换为近似服从自由度为30的
,变换为近似服从自由度为30的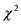 分布的统计量,
分布的统计量,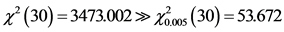 ,即Bayes判别函数耕地地力等级分类效
,即Bayes判别函数耕地地力等级分类效
果显著的概率为99.5%。对每两个耕地地力等级之间差异的显著性进行检验,构造服从分子自由度为10、分母自由度为5909的F分布的统计量,1等到4等地力的每两个总体之间统计结果如表4。
查F分布临界值表, ,远小于表3中每2个地力等级之间的计算值,故认为研究区耕地评价单元的被归入明显不同的地力等级的概率为99%。综上所述,本研究构建的Bayes判别函数对总体做到最优划分。为进一步对判别结果进行分析,从而证明Bayes判别函数应用于耕地地力评价的有效性,现随机抽取20个样本的判别结果与原始数据对比见表5。
,远小于表3中每2个地力等级之间的计算值,故认为研究区耕地评价单元的被归入明显不同的地力等级的概率为99%。综上所述,本研究构建的Bayes判别函数对总体做到最优划分。为进一步对判别结果进行分析,从而证明Bayes判别函数应用于耕地地力评价的有效性,现随机抽取20个样本的判别结果与原始数据对比见表5。
**表示判别结果与原始资料不一致的样本。如表5所呈现,评价单元样本代入Bayes判别函数结果最大,落入该函数对应的总体类别的后验概率最大,这一类别即为样本单元的地力等级。随机抽取20个样本单元,有2个显示错判,原因分析如下:
1) 本研究采用的Bayes判别法考虑了各耕地评价单元的先验概率,根据抽取的待测评价单元属性特征来修正判别分析前已有的认识,从而得出后验概率;而测土配方施肥项目开展的辉县市耕地地力评价则不需要依赖任何先验描述,受先验概率的影响,二者的评价结果难免会有所不同。
2) 测土配方施肥项目开展的辉县市耕地地力评价划分级别的方法,是用评价单元数与耕地地力综合指数制作累积频率曲线图,根据单元综合指数的分布频率,在频率曲线图的突变处划分级别。本研究通过机器学习建立Bayes判别函数,将样本数据代入函数,根据函数值大小判断样本所属地力等级,避免前者方法在累积频率曲线突变临界点附近样本归属难以取舍,操作过程也更为简便。
故出现Bayes判别结果与原始资料不一致属正常现象,根据判别函数的检验和回代法的验证,Bayes判别用于耕地地力等级预测是可行、有效的。
4. 主要结论
1) 河南省辉县市的案例研究表明,Bayes判别分析算法的最大优势是可以用于多组判别问题,在多指标、多因素分类系统的样本归属判别领域具有巨大的应用潜力,非常适用于区域耕地评价单元的地力等级归属判别,具有相对简捷、高效、精准的特点。
2) Bayes判别分析算法在研究对象的变量指标较多时,不能逐步进行筛选,剔除对总体影响不大、没有统计意义的变量,只能人为选择有用的评价指标,本文案例是基于特定范围内(完整的县域)、特定气候(一般来说,一个县域内的气候特征是基本相似的)条件下研究耕地生产力高低,若延伸到大地域范围,必然联系实际对评价指标进行增加或删减。可结合逐步判别法,利用其对评价指标有进有出的筛选,找出与研究区域关系最密切的评价指标。

Table 3. The results of Bayes discriminant analysisfor cultivated land fertilityin the study area
表3. 研究区耕地地力等级判别结果

Table 4. The calculation results of F distribution between levels of cultivated land
表4. 各等级耕地间F分布计算结果

Table 5. The random sampling of Bayes discriminant analysis results
表5. 随机抽取Bayes判别分析结果
3) Bayes判别分析需要考虑研究对象的先验概率和错判损失,这些因素对实验结果的影响大小仍有待考证,有些试验中先验概率和错判损失直接可以忽略,本研究则忽略了错判损失这一条件,找到一种使二者最大限度发挥作用的计算方法很有必要,Bayes判别算法仍有待改良。
基金项目
国家自然科学基金项目“基于分类距离–环境协变量回归模型的土壤数字化制图研究”(40971128)。