1. 引言
旋翼飞行器作为无人飞行器的一种,由于其具有简单的机械结构,灵活的机动能力,操控方便,能实现小范围内升降,能够很好的在复杂多变且空间较小的环境中飞行,因此在军事、民事方面的应用逐渐增多 [1] [2] 。精确的定位信息是旋翼飞行器在复杂环境中执行导航、路径规划等任务的基础 [3] ,大多数室外情况是依靠GPS来提供准确的位置,但是因为室内GPS信号不好,很难接收到GPS的信息,因此需要用其它传感器来提供位置信息 [4] 。目前,在室内用来作为提供位置信息的传感器主要有视觉传感器、红外传感器和激光测距仪 [5] 。视觉传感器模拟人体的双目,一般比较小,易于安装,但是它的动态性能差,处理时间较长,不利于实时处理,不利于旋翼飞行器对于位置的实时获取 [6] 。红外传感器利用红外线来感知周围环境,物体的颜色、周围的光线等可能引起红外传感器的测量误差,因此受环境的影响较大,从而使计算得到的位置的误差变大 [7] 。激光测距仪通过激光来感知周围环境,环境对于激光的影响较小,因此激光测距仪测距的精度很高,激光测距仪获取周围环境的信息非常快,有助于快速估计旋翼飞行器的位置 [8] ,因此本文选择使用激光测距仪作为提供位置信息的传感器。
本文通过使用激光测距仪来获取周围环境信息,并通过ICP算法解算出两个时刻的位移,从而迭代出当前时刻的位置,但是由于ICP算法每次解算出来的位置变化量都有误差,随着迭代次数的增多,会造成位置的误差逐渐变大,使得计算出的旋翼飞行器的位置与实际位置有很大的偏差,因此需要提高定位精度 [9] 。目前提高定位精度的算法主要有EKF [10] [11] 、粒子滤波(PF) [12] [13] 和图优化(Graph-SLAM) [14] 。EKF算法结合卡尔曼滤波的思想,对非线性系统线性化,然后对线性化后的系统用卡尔曼滤波进行滤波 [15] 。PF是对事件的后验概率用粒子集表示,粒子越集中的地方概率越大,越有可能代表旋翼飞行器的位置 [16] 。Graph-SLAM是通过旋翼飞行器的位置和周围环境的特征作为节点,它们之间通过一系列的关系式连接,表示它们之间的关系,通过当前时刻位置与节点之间的关系,使得当前时刻的位置达到最优 [17] 。但是PF、Graph-SLAM计算量太大 [18] ,不利于实时实现,而EKF算法的计算量相对较小,能够比较快速的估计旋翼飞行器的位置,因此本文选择EKF算法。
2. 坐标系的建立
2.1. 机体坐标系
激光测距仪(UTM30-LX)获取的数据是周围环境距离测距仪中心的距离,它的测量范围为270˚,角分辨率为0.25˚,因此周围环境在激光测距仪记录数据中可以表示成一系列点,记为point 0~point 1080,选择激光测距仪的中心为坐标原点,测量区域的角平分线作为测距仪坐标系y轴方向,建立二维右手坐标系,如图1所示。激光测距仪测得的数据可以写成(
,
),为同一次扫描中point i与point 0之间的夹角,因此需要对初始数据进行转换,转换公式如下:
(1)
,
是机体坐标系下x, y的坐标值。
2.2. 大地坐标系
当旋翼飞行器起飞时,以此时的机体坐标系对大地坐标系进行定义。因此,两个坐标系之间的转换关系可表示为:
(2)
,
表示大地坐标系下的x, y的坐标值(图2)。
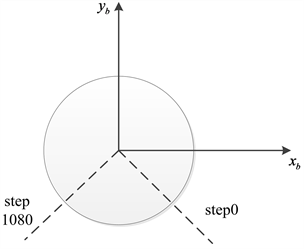
Figure 1. Curve: sketch map of body coordinate axis
图1. 机体坐标轴示意图
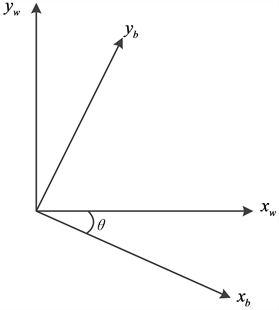
Figure 2. Curve: The relation between body coordinate and ground coordinate
图2. 机体坐标与地面坐标关系图
3. 环境中特征线段的提取
在线段提取之前,需要对激光测距仪的数据进行处理,根据公式(1),将每个数据点转换为机体坐标系下的坐标值,并对扫描仪的数据进行分割,即当两个扫描点之间的距离大于一个阈值(根据实际的经验选择合适的阈值)时,一个新的点集S产生。这些点集可以被写成:
因为本文EKF需要用到线段特征,所以采用split-merge [19] 算法对点集
进行线段的提取如图3所示,具体过程如下:
(1) 根据实际需要,确定一个点和线段关系的阈值。
(2) 点集
作为待处理数据点,连接待处理数据点的起始点和终止点,建立一个线段的模型。
(3) 找到待处理数据点中其它数据点距离线段的距离,记录其最大值,判断这个最大值与阈值的关系,如果最大值小于阈值,则不进行分割,否则,把线段分为两部分。
(4) 判断点集
中的线段是否处理完,如果没有,跳到第(2)步。
4. 改进的EKF算法
4.1. 特征表示与选择
提取出的线段可以用(r, α, l)表示(图4),r表示坐标原点到直线的距离,α表示线段的垂线与x轴的夹角,l表示线段的长度。当线段长度太小,拟合线段方程时,会造成r, α与实际有较大的误差,因此线段的长度不能太小,本文选择lmin = 0.8 m。
4.2. 模型的建立
旋翼飞行器水平面和垂直平面之间的运动模型分析是可以解耦的。本文基于水平方向的避障功能,只考虑水平面内的运动特性,因此,对于EKF算法模型的建立只考虑水平面,假设旋翼飞行器的飞行高度保持不变。
4.2.1. 观测模型的建立
本文通过对扫描仪离散数据进行处理,提取出周围环境的线段信息,并以此建立观测模型如下 [20] :
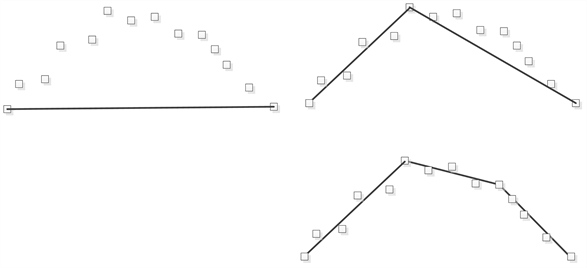
Figure 3. Curve: Sketch map of line segment extraction
图3. 线段提取示意图
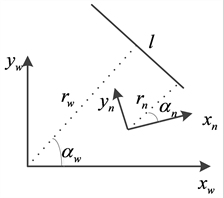
Figure 4. Curve: the definition of line in body and ground coordinates, respectively
图4. 直线分别在机体坐标系和大地坐标系下的定义
(3)
式中,
表示观测模型,
表示大地坐标系下的坐标值,M是线段的总条数,i表示第i条线段,
表示机体坐标系偏离大地坐标系的角度,即偏航角,
表示当前时刻的位置与大地坐标系x轴之间的夹角。
旋翼飞行器的飞控有提供偏航角的信息,且偏航角的精度较高,因此可以用飞控提供的偏航角信息,因此,观测模型可以简化为:
(4)
由公式(4)可得观测矩阵:
(5)
其中
使
,
,EKF测量更新过程为
(6)
式中,i = 1, 2, 3, ···, vmax, vmax为当前能匹配到的直线的最大数量。迭代结束后令
作为下一次预测输入。
4.2.2. 过程模型的建立
为了进行迭代更新,需要对旋翼无人飞行器的位置进行估计。本文采用ICP算法计算上一个时刻和当前时刻的位移变化,从而迭代出旋翼的位置,因此,过程模型如下:
(7)
式中,x(k − 1), x(k)分别表示第k − 1, k时刻旋翼飞行器在大地坐标系下的x轴坐标,y(k − 1), y(k)分别表示第k − 1, k时刻旋翼飞行器在大地坐标系下的y轴坐标,
为旋翼飞行器的偏航角,
,
分别表示旋翼从k − 1时刻到k时刻的位移变化量。
5. 实验结果分析
在旋翼飞行器上安装好激光测距仪,控制旋翼飞行一个简单的轨迹,同时通过VICON记录旋翼的位置(VICON对位置测量的精度可以达到1 mm)。实验结果如下:
从图5可以看出,在运动过程中,ICP算法计算出来的位置与VICON计算出来的位置运动趋势基本一致,导致出现差异的原因是激光是运动的,相邻的两个时刻扫描到的环境不是完全相同,这会造成ICP算法对位置估计的不准确,随着时间的增长,迭代次数增多,最终造成与实际的位置有比较大的差距。
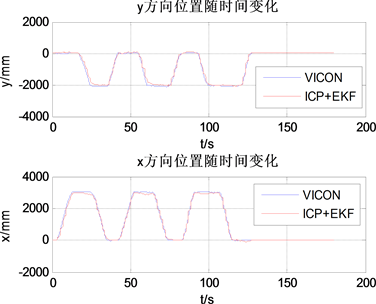
Figure 6. Curve: The position of the x direction and the position of the y direction versus time
图6. x方向位置和y方向位置随时间变化图
从图5和图6可以看出,EKF算法计算的位置基本上与VICON的位置基本保持一致,计算出来的位置都能跟的上实际位置的变化,且不会出现太大的误差,同时从图6的最后一段可以看出,随着旋翼飞行器静止之后,EKF计算出来的位置基本与VICON的一致,说明当旋翼飞行器不移动时,随着EKF对位置的校正,误差会越来越小。
6. 结论
本文首先通过ICP算法对每一个时刻的位移进行估计,然后通过上位机对扫描仪的数据进行处理,提取出线段特征,并对线段特征进行匹配,并设计EKF滤波器对旋翼飞行器的位置进行校正,最终和VICON的数据进行比较。从实验结果可知,本文通过使用EKF算法对ICP计算出来的位置进行校正,提高了位置的精度,能够比较快速的跟踪上旋翼飞行器位置的变化。
基金项目
国家自然科学基金面上项目(No. 61573186)。