1. 引言
构形的存在性问题是有限几何领域内一个主要的研究课题,其研究方法和研究结果已在组合学、射影几何学、仿射几何学、拓扑学等领域得到广泛的应用 [1] [2] [3] 。特别是在射影几何学中,其研究方法对不同维数射影平面的研究起到至关重要的作用。
历史上,数学家们对构形的存在性问题进行过研究。1876年,Reye首次提出构形的概念 [4] [5] ,即构形是点和线之间满足某些条件的有限关联结构。随后,Reye证明了
构形是存在的。数十年后,Martinetti用递归法验证了
构形的存在性 [6] 。1892年,意大利数学家Fano给出了含有6条公理的公理系统 [7] ,并证明了73构形存在性问题。近年来,许多专家和学者提出了多种验证点线数较小的构形存在性问题的方法,并取得了丰硕的成果 [8] [9] [10] 。
随着构形中点线数目不断增多,构形存在性问题的验证就会变得十分困难。为此,我们提出利用计算机对此问题进行机器验证的思想。在本文中,我们尝试用Alloy分析器 [11] 来验证一个比较简单的构形存在性问题,即:73构形的存在性问题。Alloy [12] [13] 是一个表达能力很强的关系逻辑建模语言,我们发现这种语言非常适合用于建模构形存在性问题。另外,Alloy的分析器是一个完全自动的模型查找工具,它能够地在有限范围内非常高效查找满足约束条件的模型。我们希望Alloy的这两个特性能对人们验证更难的构形存在性问题有所帮助,更希望它能够成为一个帮助人们攻克构形存在性猜想的利器。
本文结构如下:第1节具体介绍73构形和构形的相关知识;第2节介绍Alloy建模语言以及Alloy分析器的分析方法;第3节对Fano公理系统进行建模,然后使用Alloy分析器对模型进行分析验证;第4节为结论,并给出有待于进一步研究的工作。
2. 相关知识
有限几何中的主要研究对象是点、线之间的关联结构,在引入关联结构的概念之后,对构形的概念作详细的介绍。
定义1 设V与B为两个不相交的集合,i为V与B之间的一个二元关系,即
,则称
为一个关联结构。V的元素叫做点,B的元素叫作直线,i叫作关联关系。设
,
,若
,则称“点p在直线B上”或“直线B经过点p”并记作pIB。
本文只讨论有限关联结构,即V与B都是有限集的关联结构。当
为有限关联结构时,常以v表示集合V的基数,以b表示集合B的基数,即
,
,并称v为V的阶。
定义2
构形是满足如下性质的有限关联结构。
1) 存在v个点和b条直线;
2) 每条直线上含有k个点,每个点经过r条直线;
3) 任意两条直线至多有一个交点,两点间至多存在一条直线。
解决
构形问题的前提是验证构形是否是存在的,下面给出构形存在性的必要条件。
引理3 若
构形存在,则以下条件成立:
1)
且
;
2)
;
3)
。
在上述定义2中,若
(即
),则称为对称构形,简记为
构形。
构形是有限几何中研究的主要问题,目前人们用不同的数学方法对
构形的存在性问题进行研究,取得了重要的成果。
本文具体研究的73构形是
构形中的一种,是最基本的构形问题。在这里,点的个数为7,线的个数为7,每条线经过3个点,每个点经过3条线。经验证,73构形满足构形存在性的必要条件。1892年,Fano给出满足73构形的图形如图1所示。
同时Fano用数学的方法对图形做进一步的分析,即得73构形的七个点分别是三角形的重心、三个顶点以及三边中点,七条线分别是三角形的三条边、三条中线以及三边中点的圆周。
由于73构形是含点个数为7的有限结构,同时Alloy分析器恰好是在有限范围内查找模型,以此我们可以用Alloy分析器来验证73构形的存在性。
3. Alloy建模语言及Alloy分析器
在前面提到的体系构架中,Alloy建模语言是公理系统形式化的表达方式,利用Alloy建模语言描述的公理系统在73构形验证的过程中具有重要的作用,下面将简单介绍Alloy建模语言。
Alloy是由MIT软件设计工作组于1997年设计出原型的,已在多个领域中应用。Alloy是基于关系的一阶逻辑语言,同时也是轻量级的、描述性的、说明性的建模语言。Alloy建模语言综合了模型检验和语义蕴含的优点,模型检验使得验证自动化,而语义蕴含使得建模语言对系统模型描述的更加简洁。这两个优点使得Alloy成为非常有效的形式化语言。
一个典型的Alloy模型是由一系列签名(signature)、域(field)、事实(fact)、谓词(predicate)和断言(assert)组成。签名表示一类原子的集合,在其中可以包含域声明(表示签名之间的关系);事实和谓词都是对签名之间的约束条件,其中事实要求签名之间的约束关系总是成立的,谓词是可以拥有参数的约束条件,它可以用于事实中;断言是系统需要满足的属性。如果我们认定的属性系统不符合,Alloy分析器就可以产生一个反例。
Alloy分析器是分析使用Alloy描述的模型的自动化分析工具。与Alloy是同时开发的,在当时只是个原型系统,功能十分有限。随着版本的增加和功能的改进,Alloy分析器已经成为一个功能强大的分析工具。更重要的是,Alloy分析器提供了可视化的模型实例来帮助建模人员分析模型,这种直观的感受是其他模型分析工具所不具备的。到目前为止,Alloy分析器已经被用于多个领域,包括网络配置 [14] ,抽象代数的群理论 [15] 等。
Alloy分析器的分析原理是约束求解的过程。无论是通过run命令查找一个实例还是通过check命令查找一个反例。所以,Alloy分析器其实是一个一阶逻辑的约束求解器。但是在Alloy分析器在实际实现中是不可能直接求解约束的,它是通过将约束转换为一个布尔表达式,然后使用现有的SAT求解器来求解该约束。SAT求解器给转换成的布尔表达式赋值来满足该布尔表达式,即通过各种赋值使得布尔表达式成立。Alloy分析器提供了MiniSat、SAT4J、Zchaff等多个SAT求解器可供选择,默认的是SAT4J求解器。
4. 模型的建立与验证
首先,我们给出有限几何的Fano公理系统。然后,使用Alloy建模语言对公理系统和需要验证的定理进行建模。最后,在计算机上用Alloy分析器对定理进行分析、验证。
Fano公理系统A由下列6条公理组成:
公理1两点确定一条直线;
公理2每条直线上至少包含3个点;
公理3平面上至少存在一条直线;
公理4不是所有的点都在同一条直线上;
公理5两条直线有且只有一个交点;
公理6每条直线上至多包含3个点。
Fano用此公理系统证明了73构形的存在性定理:
定理平面上存在7个点,存在7条直线。
Veblen证明了73构形中的七条线不能都用直线画出,须含有一条曲线。但它并不影响结果,只是表示点线之间的关联结构,满足构形的定义。即图1所示。
由Alloy建模语言的特点,我们将公理形式化。公理系统的实质是点集、线集以及点线之间的关联关系(点在线上或者说线包含点),首先我们可以定义点集,线集为签名,并将点线之间的关系作为域声明给出,同时约束点和线在构形中,即:

其次,约束完点线后,我们知道点线之间必须满足所有的公理条件。因为公理总是成立的,所以我们将公理约束在事实中,即:
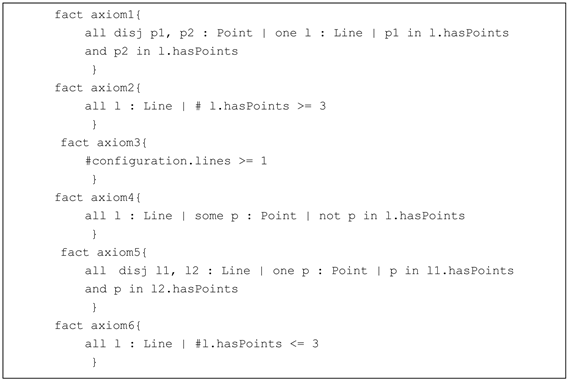
最后,我们使用断言表述定理为:

check命令用于检测断言在规定的范围内是否成立,若断言成立,系统不会产生反例;若断言不成立,系统会产生一个违反断言的实例,即反例。这样我们可以用check命令来验证所需要的定理是否成立。如果出现反例,我们可根据提供的反例快速找到错误的根源。
要注意的是,通常情况下,若没有出现反例,并不能表示就没有反例。但对于每个属性的验证是在一定范围内对所有的实例进行穷举式的检查,所以若没有出现反例时,就可以判断在该范围内所有的实例这个属性是成立的。另外,根据Alloy分析器针对小范围假设原理 [16] 得到的结果显示,大部分的错误在小范围内的实例中就可以检查出来,因此我们可以将要验证的范围进行扩大,若仍没有反例则我们可以得到经过验证后的定理属性基本是成立的。
基于此,我们不断扩大范围,重复做大量实验,得到结果如表1。

Table 1. Theorem property range validation table
表1. 定理属性范围验证表
则由小范围假设原理,可以验证该定理是可行的。
根据需求,我们可以将断言改为谓词。在Alloy分析器中run命令是用于查找满足属性的实例是否存在,因此我们可以应用run命令来查找实例,即:

运行后产生的实例如图2所示。
它包含7点7线,同时满足每条线上有3个点,每个点经过3条直线。分析后即为著名的73构形,即图1。
5. 结语
虽然73构形存在性问题是有限几何中一个比较简单的问题,数学家们早已对此问题给出了严格的数学证明,但我们使用Alloy分析器给出了一种新的机器验证方法。虽然我们的方法并不完备,不能代替严格的数学证明,但却为更难的构形存在性问题提供了一种新的求解思路。