1. 引言
目前高分辨率光学遥感通常采用TDI-CCD线阵推扫成像技术,通过对同一目标多次曝光的工作原理使得焦平面上总的曝光时间增加,从而解决了航天相机采用小孔径时,光学系统能量不足,从而获得足够的光点灵敏度和信噪比 [1] 。根据TDI-CCD成像原理,推扫方向应当与目标点的像移方向一致,像移速度大小与CCD相机的电荷行转移速度相匹配 [2] [3] ,否则成像的调制传递函数(MTF)将下降,图像变得模糊 [4] 。但是,卫星姿态机动过程中采用的同时进行成像的动态成像的方式,会造成光学像面对地空间方位发生变化,导致拍摄物体在像面转动角度即像移速度发生变化,进而造成相机的积分时间变化,从而影响成像质量,形成像移 [5] 。目前,总体参数对像移速度和偏流角影响的研究主要在于轨道高度的变化,对于姿态的影响情况并没有很完善。
本文采用太阳同步轨道,以TDICCD作为光学有效载荷,针对敏捷卫星在不同姿态角度下多种成像模式,分析对应的像移速度和偏流角数学模型,得到对应表达式,对敏捷成像的研究具有重要意义。
2. 卫星总体参数对像移的影响分析
敏捷卫星在成像过程中,星体相对于地面具有各种方式的运动。如地球自转造成的相对运动,卫星自身轨道运动,姿态运动,卫星的振动等 [6] 。敏捷卫星成像过程中会采用大角度姿态机动,目标点与星下点的偏移量较大,导致轨道高度与光轴长度存在一定的偏差,同时不同姿态角的组合导致的像移方向在焦面上也会不同,就需要根据不同成像条件(星下点成像、俯仰成像、侧摆成像、俯仰侧摆成像),研究所产生的像移分布情况。
影响TDI-CCD像移的主要因素有:轨道倾角、轨道高度、地形高度、地球自转速度、星下点的经纬度、卫星的姿态角、卫星的姿态角速度、相机的焦距、相机安装精度和抖动等。这里将问题简化。不考虑地形高度和相机自身的问题,只考虑卫星总体中的各因素(轨道高度以及姿态角)对像移的影响。
2.1. 星下点成像模式下的像移速度
2.1.1. 星下点成像模型
高分辨率遥感卫星大多采用太阳同步圆轨道,表示为:轨道高度h、偏心率e、轨道倾角i、升交点赤经
、近地点幅角u、过升交点时刻
。
卫星轨道角速度,
星下点纬度。星地关系如图1。
2.1.2. 轨道运动产生的像移速度
卫星的轨道运动是焦面相对于地面最直观的运动,其产生像移的原理如图2。
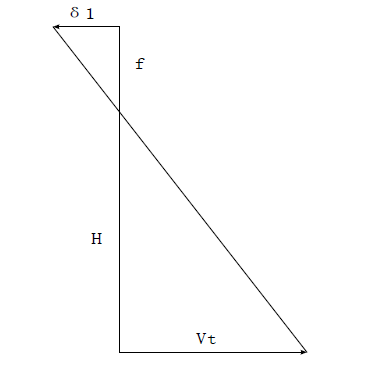
Figure 2. Principle diagram of orbit motion image shift
图2. 轨道运动像移原理图
其中,L等于H (卫星轨道高度),
星下点速度(
)。
为相机积分时间。基于相似三角形比例关系,由轨道运动造成的像移速度
,像点在图像上的位置关系如图3:
(1)
像点在图像上的位置关系如图3。
点1表示静止时像点在图像上的位置,点2表示在曝光时间内发生相对运动后像点在图像上的位置。
2.1.3. 地球自转产生的像移速度
卫星在高空轨道飞行时,由于地球自转,将造成的卫星与地面目标的相对运动。这种相对运动就会形成像移,降低成像质量。由地球自转引起的像移速度
公式如下:
(2)
像点在图像上的位置如图4。
2.2. 侧摆姿态机动成像模型
为拓宽卫星成像幅宽,常需要利用卫星的滚动实现侧摆成像从而拓宽成像幅宽。相机滚动成像的星地关系图如图5。
2.2.1. 轨道运动产生的像移速度
其中
(b为地球半径量度时地心角
所对应的弧长),由于卫星侧摆,目标点的纬度发生了变化,由
转移到了
,目标点的轨道运动的速度为
。由于侧摆
,光轴长度发生变化,在进行物面到焦面的坐标变换时,需要考虑L的变化。
(3)
其中,
,
2.2.2. 地球自转产生的像移速度
由于侧摆成像,目标点由星下点S偏移到点T,纬度由
变为
,此时目标点T处的地球自转线速度为
,与轨道运动所成夹角由初始的轨道倾角i转变成了等效轨道倾角i2。
为求得
,先利用
求得目标点纬度
,针对不同轨道类型以及目标点与星下点相对位置,

Figure 3. Diagram of image shift direction
图3. 像移方向示意图
Figure 4. Diagram of image shift direction
图4. 像移方向示意图
取值不同。根据球面三角形相关公式求得:
(4)
式中,±的选取可根据实际物理过程决定,顺行轨道,目标点纬度高于星下点纬度时取+,低于星下点纬度时取—;对于逆行轨道,规则相反。
在球面直角
中,升交点幅角u:
(5)
从而求得目标点T的等效升交点幅角u2和等效的轨道倾角i2:
(6)
(7)
由地球自转在焦面所形成的像移速度为:
(8)
2.3. 俯仰姿态机动后成像模型
为获得立体成像效果,需要卫星进行俯仰成像,通过卫星的俯仰姿态机动实现的。相机俯仰偏移的星地关系图如图6。
2.3.1. 轨道运动产生的像移速度
卫星俯仰偏移后,成像目标点由S转移到了新目标点T。因俯仰方向发生在飞行方向,故点T位于星下点轨迹上。由于采用的是太阳同步圆轨道,S点与T点的轨道角速度都是一致的,所以T点由轨道运动造成的像移与星下点的情况相同。
(9)
其中,俯仰会将视距增大,
。
2.3.2 地球自转产生的像移速度
计算由地球自转所产生的像移,就需要计算新目标点T的纬度。利用球面三角形
,根据边的余弦定理,得到:
(10)
c在
利用正弦定理求得,
(11)
故此,由地球自转产生的像移速度:
(12)
仅俯仰成像时,等效轨道倾角并没有变化。与轨道运动所造成的像移夹角仍为轨道倾角i。
2.4. 侧摆加俯仰姿态机动后成像模型
敏捷卫星成像时,卫星需要同时进行俯仰和滚动方向上的机动,从上述单一的俯仰和偏航成像模型推导可以发现,主要还是需要得到最终成像目标点的纬度以及对应的地心幅角。星地关系图如图7。
2.4.1. 轨道运动产生的像移速度
由于存在侧摆,目标点T并不在星下点轨迹上,所以轨道运动对目标点T的影响会因为存在角度b的偏移,
(13)
由卫星运动引起的成像点牵连速度:
(14)
2.4.2. 地球自转产生的像移速度
目标点T处的地球自转速度就需要考虑目标点T的纬度,计算过程思路:假设姿态机动过程为先俯仰机动角度θ,再进行侧摆机动角度ϕ,可以得到各自对应的地心角,又星下点S的纬度,先求得S1的纬度,作为中介,进而求得目标点T的纬度。
(15)
(16)
(17)
(18)
(19)
(20)
(21)
在卫星成像目标点的地球自转速度为
(22)
地球自转速度引起的像移与轨道运动引起像移的夹角为轨道倾角i。
3. 仿真分析
光学遥感卫星大多采用太阳同步圆轨道,本次仿真基于以下条件:轨道高度
,地球半径
,轨道倾角
,最大姿态侧摆角
,最大姿态俯仰角
,星下点地心纬度范围
。相机焦距
,像元尺寸
。
根据上述公式,考虑到卫星最大姿态角度为45˚,仿真分析在星下点、侧摆45˚俯仰0˚、侧摆0˚俯仰45˚以及侧摆45˚俯仰45˚情况下,在任意位置的卫星的像移速度和偏流角的分布图,如图1,同时仿真分析在相同的姿态角的前提下,卫星的轨道高度对像移速度和偏流角的影响情况。
姿态机动对地成像,仿真结果分析如下:
该仿真结果,与参考文献中李永昌 [6] 的结果变化规律是一致的。故而仿真实验结果可信。
在同一位置下,采用不同姿态角的组合成像,所造成的像移速度存在明显差异,变化范围由0.1254到0.0132 m/s。图8中可以读出,星下点像移速度 > 侧摆45˚像移速度 > 俯仰45˚像移速度 > 侧摆45˚俯仰45˚像移速度。同时根据俯仰&侧摆&像移速度三维曲面图可以看出,只要存在一定姿态角,像移速度就会呈现下降趋势。根据之前数学模型,当存在俯仰角时,卫星到目标点的距离变大,卫星轨道运动形成的像移速度与像平面存在一定的夹角,故而投影到像面上的速度减小;当存在滚动角时,卫星到目标点距离增大,导致速高比减小,像移速度减小。因此,姿态机动会导致像移速度减小。
由图8可看出星下点成像时,整个像移速度类似于正弦函数,呈周期性,考虑到没有姿态角机动时,星下点轨迹是经过地心的圆,卫星与星下点的距离是固定的,由于地球自转所引起的像移速度分量在星下点成像时呈现正弦周期运动,故而总像移速度呈周期性变化。
俯仰运动时,光轴指向轨迹根据数学模型可以看出同样是经过地心的圆,只是因为存在俯仰角,光轴长度增大,导致整个正弦曲线数值上有所变小;滚动运动时,光轴指向轨迹只是一个不经过圆心的校园,卫星在整个运行过程中,目标点的地理纬度时不同的,地心角在不断变化,像移速度在呈现非周期性变化。
图8右侧的偏流角中,正负表示偏流角的方向,无姿态机动是,偏流角最大可达5.0952˚,最小值为−5.0952˚;俯仰成像时,偏流角的峰值变大,达到7.0664˚,因为卫星轨道运动所引起的速度偏移量随着
俯仰角的增大而减小;仅有偏移运动时,偏流角的峰值减小,仅为3.5002˚,因为偏移侧摆角的增大,像平面与地平面的夹角变大,地球自转所引起的像移速度在Y轴上的投影就会减小,导致偏流角变小;图9中看出,俯仰侧摆成像时,偏流角的正负方向的变化幅度并不对称,最大值为4.3449˚,最小值为−7.1808°,通过分析对应成像数学模型可以看出,当侧摆俯仰同时存在时,目标点纬度与侧摆角和俯仰角并不是线性可解析的关系,存在着一定的耦合,故而导致偏流角的变化并不是对称的。
从仿真图10中可以看出,随着轨道高度的增大,导致速高比降低,进而像移速度减小,根据数学模型可以看出,整个像移速度与到目标点的距离成反比,从仿真图像中也可以印证这一点;同时由于轨道

Figure 8. Image shift speed and drift angle at different attitude angles
图8. 不同姿态角组合下的像移速度和偏流角
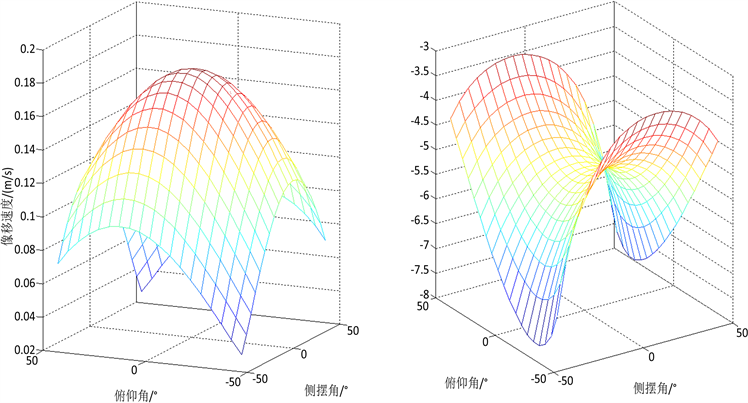
Figure 9. Image shift speed & deviation angle vs. attitude angle diagram
图9. 像移速度&偏流角与姿态角关系图

Figure 10. Image shift speed & deviation angle vs. height
图10. 像移速度&偏流角与轨道高度关系图
高度的增大,卫星轨道运动在线面上的线速度增大,同样的星下点位置,同样的姿态角情况下,投影在横向上的像移速度会增大,导致偏流角随着轨道高度变化线性变大。
4. 结束语
本文主要对敏捷卫星姿态机动的成像模型进行了推导,给出了在仅俯仰、仅滚动以及俯仰滚动存在下时,卫星轨道运动以及地球自转等主要因素对像移速度、偏流角的计算公式以及对应的仿真结果。仿真结果表明,在最大姿态机动角为45°的成像下,像移速度在0.1254到0.0132 m/s范围内变化,在不同姿态下,像移速度的幅值是不同的,故而姿态变化是导致像面像移速度改变的主要因素,轨道高度的变化引起速高比的变化,轨道高度越高,像移速度越小;偏流角的变化范围在−7.1808˚到5.0952˚范围内变化,尤其是当俯仰角和侧摆角同时存在时,偏流角的正负幅值并不是对称的,卫星偏流角控制时需要实时动态更新调试以适应新的成像姿态。本文对多种姿态情况下的成像所形成的像移速度和偏流角进行分析,可以为后续敏捷卫星在复杂姿态下的成像提供参考。