1. 引言
GPS高程测量是高程测量中非常重要的一种方法,其测得的是大地高,需要由大地高向常用的正常高进行转换 [1] - [6] 。很多文献中多采用曲面拟合的方法,建立一个拟合面来代替拟合区域的似大地水准面 [7] [8] [9] [10] 。这种方法可以获得一个比较接近的高程异常值,但二次曲面拟合的拟合面必然会遵循二次曲面的结构趋势,无法根据不同的拟合点以及拟合区域灵活地进行调整。为了对拟合点中存在的随机性残差进行改进,本文引入了最小二乘配置法模型。最小二乘配置法不仅能考虑高程异常的趋势性,还能根据区域内的个别变化考虑其随机性,在一些地形复杂、地表崎岖、区域面积较大、拟合跨度较长的区域内,能够得到很好的用于实际工作的拟合结果 [11] [12] [13] 。本文针对类似的复杂区域情况,在拟合模型改进、模型符合精度方面展开探讨。
2. 高程异常拟合模型
2.1. 曲面拟合
多项式拟合即在拟合区域中根据已知水准点数据构造一个曲面来代表拟合区域的似大地水准面,函数模型为:
(1)
式中:
为高程异常;
为误差;
为拟合多项式,见式(2):
 (2)
(2)
式中:
为未知系数;x、y为拟合点的经纬度;K为多余条件数。采用了六参数多项式,即二次曲面多项式,利用选取的拟合点求得待定系数。计算未知参数,建立超定方程组,使用最小二乘法求其最小二乘解,公式见式(3):
(3)
式中:X是六参数多项式的各项未知数;Y是高程异常值。将式(2)带入式(1)求得高程异常值,实现大地高向正常高的转换。
2.2. 最小二乘配置法
最小二乘配置法的数学模型如下:
(4)
式中:L为已测点高程异常的观测值;B为已知系数矩阵,具体数值取决于选取的拟合函数类型,采用的最小二乘配置是基于二次曲面拟合的,此处为公式(3)中B;X为非随机变量; ,E为单位矩阵;S为高程异常与其趋势面的差值;
为观测信号;
为观测信号的噪声。根据上式写出误差方程:
,E为单位矩阵;S为高程异常与其趋势面的差值;
为观测信号;
为观测信号的噪声。根据上式写出误差方程:
(5)
式中:V为改正数;
为X的估计值; 为Z的估计值。上式按照最小二乘准则化简后得
为Z的估计值。上式按照最小二乘准则化简后得 和
的计算式为:
和
的计算式为:
(6)
(7)
式中:
为L的自协方差阵;
为 的估计值;
为
和S的协方差阵。
的估计值;
为
和S的协方差阵。
由此得待测点高程异常平均值为:
(8)
式中:
为待测点高程异常的估计值。
3. 算例分析
选用数据为某煤矿的22个点的D级GPS控制点成果,所有测点均已联测四等水准。已知22点中选取18点作为拟合点建立函数模型,其余4点作为检核点用于检核模型误差。18个拟合点的大地高、正常高如图1所示。
GPS网点分布如图2所示,其中黑色方块点为检核点,已在图中标明检核点点号,其余点为拟合点。
两种模型的拟合结果如表1所示。
两种模型的残差对比如图3所示,两种模型的拟合残差如图4所示。
对上图表进行结果分析时,需要从内符合精度与外符合精度两方面进行分析:将已知的拟合点数据带入到已建立的模型中,得到的残差值即为内符合精度;将已知的检核点数据带入到已建立的模型中,得到的残差值即为外符合精度。两者区别在于,已建立的模型是建立在拟合点数据的基础上,而与检核点数据无关。
由上图表计算得曲面拟合模型内符合精度为0.024 m,最小二乘配置模型内符合精度为0.0038 m;曲面拟合模型外符合精度为0.036 m,最小二乘配置模型外符合精度为0.0028 m。结果表明,无论对于模型内的拟合点还是模型外的检核点,最小二乘配置模型的残差明显较低,残差值相对曲面拟合模型降低了一个数量级;其内外符合精度都有较大的提高;其模型的残差明显小于二次曲面拟合模型,且各点精度

Figure 2. GPS network distribution map
图2. GPS网点分布图
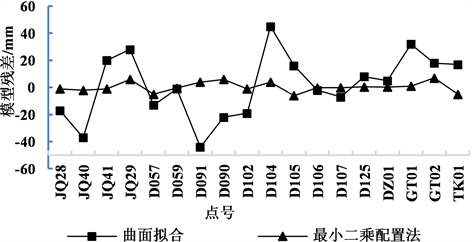
Figure 3. Internal model residual comparison
图3. 内符合的模型残差对比

Figure 4. External fit fitting residual comparison
图4. 外符合的拟合残差对比
分布较为平均,没有太大起伏。二次曲面模型残差较大,究其原因,主要有以下几点:
1) 二次曲面模型仅考虑拟合点数据的趋势性,未考虑个别区域的随机性;
2) 单纯地选取某个次数的曲面模型时,拟合面一定符合该次数曲面模型的结构特征,这会使得某些处于拟合点之间的拟合区域不能很好地符合拟合数据的特征;
3) 二次曲面模型未使用计算各点协方差,使得计算结果未能很好地考虑各点之间的关联性。
4. 结论
本文给出了曲面拟合模型和最小二乘配置模型,利用某矿区的GPS数据与水准数据进行了相关的验证。结果表明,最小二乘配置模型拟合效果明显优于曲面拟合模型,残差值较低,内外符合精度均有数量级的提升,拟合结果可以用于相关实际工作。尽管模型达到一定拟合精度,但模型拟合到的水准面不一定是准确的,实际工作中需要同时综合内、外符合精度及残差分析拟合效果,才能更准确得出拟合能力。