1. 引言
对流占优方程的间断初值问题一直以来都是数值计算的重要内容。线性格式有中心差分格式CD (Central Difference),二阶迎风格式SOU (Second-order Upwind),QUICK [1] (Quadratic Upstream Interpolation for Convective Kinematics)对于光滑初值都能达到二阶及以上的精度。对于间断初值问题,线性格式由于不满足对流有界性,容易引起非物理振荡。为此Gaskell和Lau提出了CBC (Convection Boundedness Criterion) [2] ,可以保证数值格式的有界性,但是未能保证数值格式的精度。为了克服这个缺点,Hou提出了BAIR [3] 准则。1983年Harten [4] 提出了TVD (Total Variation Diminishing)格式,满足了有界性的要求且具有高分辨率的优点,在间断处和极值点处却达不到三阶及以上的精度,尤其在极值点附近由于差分格式的解只具有一阶精度。考虑到前面几个格式的不足,本文提出了格式一种非线性QUICK格式,使得在间断处利用一阶迎风格式,在连续处利用三阶QUICK格式。于是如何判断间断与光滑成了关键问题。本文分析了 [5] 中的光滑因子的特性,考虑到 [6] 中关于平滑度度量的不足,即对于间断和光滑极值不能够明确的界定,于是本文设计了一种能够有效捕捉间断位置的方法,使得对间断和光滑极值的判断清晰而准确。通过算例分析,对于光滑解,达到一致高精度。对于间断解,可由有效抑制数值振荡,逼近效果良好。
本文整体结构安排如下:第一节本文用有限体积格式对守恒律方程进行空间离散,用Lax-Friedrichs [7] 型数值流通量对通量进行数值逼近。然后通过间断阈值对解的间断与光滑处进行判定,构造了非线性加权新格式来离散对流项。第二节对时间进行离散。第三节为一些数值算例及其结果的分析与讨论。第四节得出结论。
2. 空间离散格式
2.1. 有限体积离散
一维守恒律方程为
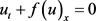
其中
为流通量。用有限体积法对(1)进行离散,首先将计算区间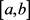 剖分为N等分,
且每个控制单元为
,其长度为
,对(1)在区间
上进行积分,则有:
剖分为N等分,
且每个控制单元为
,其长度为
,对(1)在区间
上进行积分,则有:
令
,称其为积分平均值,于是可以得到
利用数值通量逼近上式如下:
其中
是
的数值近似,数值流通量
来近似逼近
,其中
Lax-Friedrichs型的数值流通量为:
(1)
其中
。
2.2. 对流项离散
本文构造了的非线性权的QUICK格式来逼近对流项
,有如下格式
(2)
(3)
其中
为权,当解在光滑区域时,此时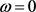 ,数值格式变为三阶QUICK格式;当解在间断区域时,此时
,数值格式变为一阶迎风格式,一阶格式可以抑制振荡,于是如何判断光滑与间断成为了关键问题。
,数值格式变为三阶QUICK格式;当解在间断区域时,此时
,数值格式变为一阶迎风格式,一阶格式可以抑制振荡,于是如何判断光滑与间断成为了关键问题。
为了有效的判断光滑与间断,使得格式在光滑处利用三阶QUICK格式,在间断处利用一阶迎风格式。根据对文献 [8] [9] [10] 里k个模板下的光滑因子
进行分析,
(4)
其中
是在k个模板
下构建的多项式。(4)右侧的积分是在
上插值多项式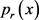 的所有导数的在
范数下的平方和。可知当
时,根据文献 [11] [12] [13] 中对光滑度的测量
,我们引入如下形式的光滑因子,
的所有导数的在
范数下的平方和。可知当
时,根据文献 [11] [12] [13] 中对光滑度的测量
,我们引入如下形式的光滑因子,
通过分析计算可知,在连续时
之间几乎相同,而在间断处
之间存在较大的变化,
对数值解的间断部分比较敏感,通过分析文献 [6] ,我们给出了的如下光滑参数:
可以很好的衡量数值解的陡度和光滑程度,在光滑处通过泰勒展开可知
,而在间断处
的值变化比较大,由于
值在间断处的变化不能够明确的界定间断与光滑,为了更加明确的判断,分析了以上的光滑因子与光滑参数的特性,我们给出
的界定值,构造出了如下间断阈值:
其中
,通过大量实验发现在间断处有
,而在光滑处有
,根据算例发现通过 与 的比较确实能够有效的判断间断与光滑区域。
3. 时间离散
对空间进行离散后得到关于时间的常微分方程组,为了保持整体格式的三阶精度,对时间利用三阶Runge-Kutta方法来进行离散,并且可以有效避免振荡,三阶Runge-Kutta格式如下:
4. 数值算例
4.1. 线性对流方程
(4)
4.1.1. 情形1
在给定初始条件
,
,利用新格式计算当
时,时间t = 0.1时的数值解,并求出格式的
误差及其精度阶(如表1),计算公式如下:
精度阶的计算公式:

Table 1. Errors and orders for schemes
表1. 格式误差与数值精度阶对比
由表可知此格式对于光滑初值条件下,新格式的数值解能够达到三阶精度,具有较高的分辨率。
4.1.2. 情形2
在给定间断复合初始条件
利用新格式计算当网格数
时,
,
,时间
时的数值解并与精确解在图1中进行比较,精确解与QUICK格式下的数值解在图2中进行比较。
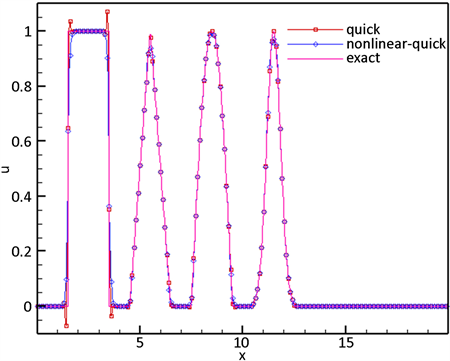
Figure 1. Numerical solution of the above two schemes and the exact solution with initial condition of composite discontinuity
图1. 间断复合初始条件下的非线性QUICK格式和QUICK格式的数值解与精确解
由图1可知,QUICK格式与非线性QUICK格式相比,QUICK格式在间断处要产生的振荡,而新格式在间断处容易避免振荡,在光滑处的逼近效果也比较好。
4.1.3. 情形3
在给定间断初始条件
,
当网格数
,新格式的数值解及QUICK格式与精确解图像如图2。
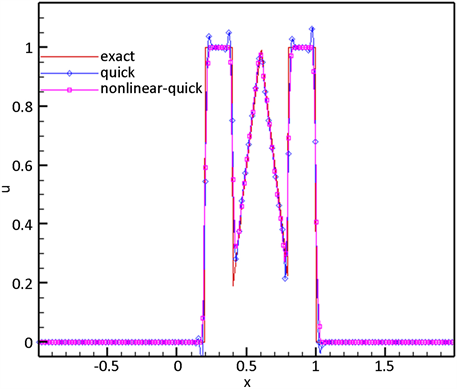
Figure 2. Numerical solution of the above two schemes and the exact solution with W-shaped initial condition
图2. 间断初始条件下的非线性QUICK格式和QUICK格式的数值解与精确解
由图2可知QUICK的数值解在间断处会产生振荡,而新格式的数值解与精确解相比较,在间断处没有振荡,相比较新格式达到了比较好的逼近效果。
4.1.4. 情形4
对于有间断及相邻近处有极值的初始条件而言,对于格式的要求比较高,对于前面提到的格式,会在间断处产生振荡,不能够很好的区分光滑极值和间断,容易混淆这两种情况,从而在极值处的逼近效果不是很理想,下面我们给出在新格式下的数值解。
在给定有间断和极值的初始条件如下
利用新格式计算当
时,时间
时的数值解和QUICK格式的数值解与精确解的比较如图3进行比较。
由图3可知,对于有光滑极值和极值邻近处有间断的初值问题,由数值解图像可知新格式无论是在间断处还是在极值点附近其逼近效果都非常好,而QUICK格式在间断处却会产生振荡,可知非线性QUICK格式比QUICK格式的逼近效果要好。
4.2. 无粘Burgers方程
无粘burgers方程解会随着时间的推移产生间断,给数值求解带来了很大困难,本文利用新格式求解此方程如下,
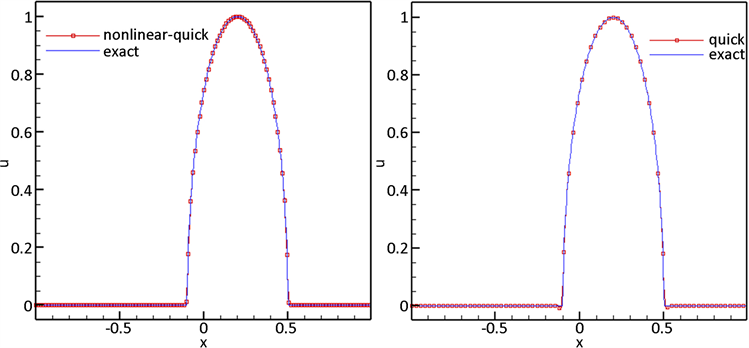
Figure 3. Numerical solution of the above two schemes and the exact solution with complicated structures
图3. 复杂结构初始条件下的非线性QUICK格式和QUICK格式的数值解与精确解
其初始条件为
,新格式的数值解图像及QUICK格式的数值解的图像如图4:
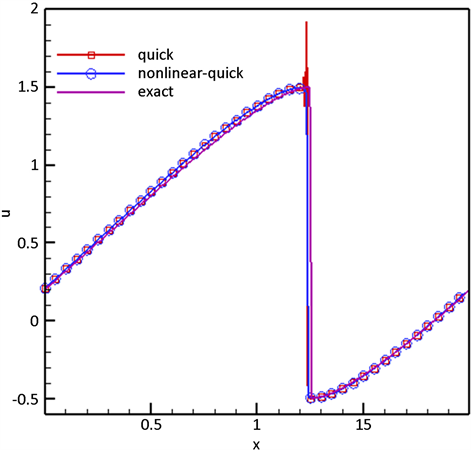
Figure 4. Numerical solution of the above two schemes and the exact solution of Burgers equation
图4. Burgers方程的非线性QUICK格式和QUICK格式的数值解与精确解
由新格式与QUICK格式的数值解与精确解的图像比较可发现,在随着时间的推移,在逼近解的间断处时,QUICK格式下的数值解会有明显的振荡,而在非线性QUICK格式下的数值解会避免振荡,有很好的逼近效果。
5. 结论
本文基于有限体积下对双曲守恒方程进行数值离散,利用三阶QUICK格式与一阶迎风格式(FOU)加权后得到新的非线性QUICK格式来逼近对流项,本文通过引入间断阈值使得对流项的离散格式在间断处利用一阶迎风格式并且在光滑处使用三阶QUICK格式,通过算例分析,对于光滑初值能够达到三阶以上精度,对于有间断和极值的初值问题也可以避免振荡,使得数值解达到了比较好的逼近效果。
基金项目
感谢内蒙古自治区研究生科研创新项目(1402020201-46)及内蒙古自然科学基金项目(2015MS0101)和内蒙古自治区人才开发基金项目(12000-1300020240)的支持。