摘要:
一个图 G 的分数荫度定义为
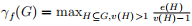
,著名的 Nash-Williams 定理指出:当且仅当
γf (G) ≤ k 时,图 G 最多能边分解为 k 个森林。对此 强九龙树猜想断言,对千任意非负整数 k 和 d 任何分数荫度至多为
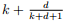
的图都能边分解为 k + 1 个森林,并且存在其中一个森林,它的每个连通分支最多包含 d 条边。在本文中,我们将
τi(G) 定义为
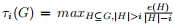
,当然,
τ1(G) =
γf (G)。对于整数 i ≥ 1,图 G 的 i-森林是图 G 的支撑森林,其至少包含了 i 个连通分支。而一个 i-树是指一个 i-森林恰好有 i 个连通分支。我们证明了,当 k = 1, d = 2 时,分数 i-荫度至多为
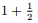
的图 G 能边分解2个 i -森林并且其中一个 i-森林,它的每个连通分支最多包含 2 条边。
Abstract:
The fractional arboricity of a loopless graph G is defined as
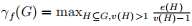
. The famous Nash-Williams theorem states that that a graph G can be decomposed into at most k forests if and only if
γf (G) ≤ k. The Strong Nine Dragon Tree Conjecture asserts that for any non-negative integer k and d, any graph with fractional arboricity at most
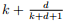
decomposes into k + 1 forests with one of them consisting of trees of sizes at most d. In this paper, we define
τi(G) as
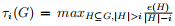
, here,
τ1(G) =
γf (G). For the integer i ≥ 1, an i-forest of a graph G is a spanning forest of G that has at least i connected components of. An i-tree means an i-forest that there are exactly i connected components. We prove that when k = 1, d = 2, a graph G with
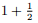
, then the graph G can be decomposed into 2 i-forests such that for one of them, each connected component contains at most 2 edges.