1. 引言
通过数学分析的知识我们知道,对于单变量函数 ,给定一个区间,如果在这个区间上函数连续,且在两端点的值异号,则在这个区间内函数至少有一个零点,即方程
在这个区间内有实根。
,给定一个区间,如果在这个区间上函数连续,且在两端点的值异号,则在这个区间内函数至少有一个零点,即方程
在这个区间内有实根。
假设函数
在区间
上连续,在
内有单根且在端点处的函数值异号,即
,
给出如下迭代格式:
如果
,则:令
,
,继续进行上式的迭代过程;如果
,则按照如下改进后的迭代格式进行:
其中参数
。改进后的格式被称为Illinois-type算法 [1] 。
2. 对参数的理解
2.1. 二分法
二分法是一种非常简单的数值方法,其基本原理是连续函数的介值定理。同上文假设的条件,计算区间
中点处的函数值
。若 则重置区间
为
(反之取另一半区间
进行),重复以上操作直至达到精度要求,根据区间套定理知如此构造的迭代序列收敛,且收敛速度与公比为
的等比数列收敛速度相同 [2] 。
则重置区间
为
(反之取另一半区间
进行),重复以上操作直至达到精度要求,根据区间套定理知如此构造的迭代序列收敛,且收敛速度与公比为
的等比数列收敛速度相同 [2] 。
2.2. 试位法
设
在闭区间
上连续且在端点处异号。以连接 与
的直线段L近似代替函数
的图像,而以L与x轴的交点坐标c作为
零点的近似。
与
的直线段L近似代替函数
的图像,而以L与x轴的交点坐标c作为
零点的近似。
根据三角形相似,可以建立求解c的方程:
整理后即得:
若
,则方程的实际根落在
或
中,选择这个区间重置原区间。重复如上过程直至
前后两次迭代结果的差小于事先设定的误差。
3. 收敛性分析
3.1. 收敛性
设
,对于迭代产生的序列
,根据试位法的迭代原则知序列
单调不减,序列
单调不增,因此收敛,分别设其极限为
,
,且有
。
1) 假设
,
都不是
的根。
存在
,正整数N,当 时,
,
。由迭代格式知:
时,
,
。由迭代格式知:
,
在
上有界,设为M。则对于任意的正整数n,都成立
因此,
从而得到
但是,既然对于任意的n,有
,这说明
,即
,
均不是方程
的根。
2) 假设
是方程的根,
不是方程的根。
根据上述公式有
而不等式右端极限存在,为0,所以有
同理,如果
是方程的根,
不是方程的根,有
3) 假设
,
都是方程的根。若
,则存在一子列
收敛到
,或有另一子列收敛到
,即
。
下面我们证明,除非
或者
是
的根,或者对于某些n,
是
的根,就有
。
假设
,对于任意
,存在正整数N,当
时有:
,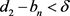
显然有,对于任意正整数n,
或
。若对某些n成立
,则:
且
。不妨设
,
。为了序列
收敛到
(
),必须有对于比n大的m,满足
,这表明:

同理,对于大于n的p,有
如此进行下去,则对于任给的
,对于
,x趋近于
。既然
不是
的根,则
,即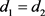 。
。
综上所述,迭代格式收敛。
3.2. 收敛速度
由上一部分证明知序列
收敛。对于充分光滑的函数
,能求得序列
收敛速度的下界 [2] 。设
连续二次可微,且在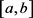 内有
不恒等于0;设
是
的零点。根据试位法的迭代格式
内有
不恒等于0;设
是
的零点。根据试位法的迭代格式
因为
根据Cauchy中值定理,存在
使得
根据Taylor公式,有
其中
介于
与
之间。结合前一个式子,则有
记
,
,
,则上式可写为
根据可微性的假设,存在正数m,M,使得对任意
,有
,
,则
用
乘不等式的两边,有
它等价于不等式
,其中
(注:这里将
也用
表示)。设初始逼近
, 满足
满足
则迭代到第k步时,
,这说明试位法是线性收敛的 [3] 。当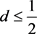 时,试位法收敛速度快于二分法。
时,试位法收敛速度快于二分法。
4. Illinois算法
4.1. 收敛性
Illinois算法很好地避免了不动点的出现,近似根从两端收敛到精确根,即迭代生成的新区间的长度
 。基于这一条件,根据区间套定理以及一致连续定理,我们给出一下证明。
。基于这一条件,根据区间套定理以及一致连续定理,我们给出一下证明。
因为函数
在
上连续,则
在
上一致连续,即:
,
,只要
,就有
。则
,
,当
,就有
。
对于上述
,
,当
时,
则
,即
因为
,
,又因为
,根据区间套定理
则
又因为
,所以
即迭代序列收敛到方程的根。
4.2. 收敛速度
仍采用上文记号
,令
由上一小节证明,
Illinois算法一次迭代包括先进行一次试位法,在进行两次修正 [4] ,则
得到Illinois算法的收敛指数 [5] 为
。即经过一次Illinois后,误差缩小为上一次的
次方。
5. 函数实例
5.1. 不动点的情况
先来看一个出现不动点的情况:
,初始区间为
。
在使用试位法求根时,出现了不动点
的情况,迭代序列从左端点收敛到
;而Illinois算法从第4次迭代开始不动点消失,迭代序列从两端收
,收敛速度快于试位法;另外,当迭代相同次数时(10次),后者精度高于前者。
5.2. 算例对比测试
选取了两个比较有代表性的算例进行了测试,将精度设定为10−15,计算结果如表1 (I代表Illinois算法,F代表试位法)。

Table 1. Comparison of examples between regular falsi method and illinois method
表1. 试位法与Illinois算法的算例对比
6. 总结
当函数接近线性时(图像上来看越接近直线),该算法的效果明显。大多数情况下,试位法的效果会明
显优于二分法。但是,如果区间
的长度比较大,曲线
在
内某一点附近一阶导数值突然急
剧增长,在这种情况下,试位法出现了一个端点总是不动的情形,因此近似根只从一端收敛到精确根,这样它减慢了收敛速度,效果反而不如二分法。尤其当初始区间很大或函数在区间内偏离线性近似很远时收敛更慢。为了消除这种情况下的负面影响,可以对试位法做相应改进,在改进的试位法中,如果一个端点重复两次或更多次作为新的含根区间的端点(称为不动点),则我们将这个点的函数值乘一个因子,使得线性插值的根更接近于精确根。这种改进真正体现了“试位”的思想。