基于非线性拟合投影寻踪模型和加速遗传算法通过Logistic回归分析一个地区供水能力

A Regional Water Supply Capacity Based on the Nonlinear Fitting of Projection Pursuit Model and Accelerating Genetic Algorithm by Logistic Regression Analysis

摘要: 本文围绕“水资源短缺及地区供水能力”问题，运用主成分分析法选取指标。建立一次线性函数规划模型和投影寻踪模型，计算得到供水能力，并用二级模糊综合评价模型Delphi法评定权重。利用logistic模型得到了地区的水状况，并且描述了这种状况对该地区公民生活的影响。本文以研究水资源供需指标体系为主线,通过对模型的精确求解,得出研究地区提供洁净水能力的等级水平、还研究了是否缺水，提出了解决缺水问题的具体措施。最后,将这个数学模型推广应用到全球，为解决全球缺水做出贡献。

Abstract: This paper studies the problem of the sustainable development of regional water resources, the evaluation of the regional water supply ability; we used principal component analysis (PCA) to affect the physical and economic indicators of water filter, using a function model of calculating water supply capacity and projection pursuit model, the secondary fuzzy comprehensive evaluation model to assess the weights. This paper uses the logistic model to obtain water conditions in the region, and describes the impact that this situation has on the civic life in the region. This paper studies the index system of supply and demand of water resources as the main line, through the precise solution of the model; the region's ability of providing clean water levels was concluded, it also studied the water shortage, put forward the specific intervention plans to solve the problem of water shortage.

1. 前言

水是人类赖以生存和发展的基础资源，是社会经济发展和繁荣的保障和支撑。地球上能供人类生活和生产之用的淡水资源仅占地球储水量的2.5%，而易于开采利用的淡水资源不足淡水总量的1%，到目前为止世界上约有3亿人处于极度缺水状态。尤其近年来，受气候变化和经济社会发展的影响，水资源短缺问题日趋严重。

本文建立了一个可以衡量一个地区的提供洁净水的能力。我们考虑了影响一个地区供水能力的诸多因素，利用主成分分析法筛选出了影响最大的两个指标：地下水储量，地表径流。又利用了一次线性函数模型计算出了供水能力，最后利用模糊综合评价法对一次线性函数模型进行评价发现该模型不能很准确地衡量一个地区为其人口提供清洁水的能力。又对模型进行了改进，提出了投影寻踪模型，这个模型可以很准确地衡量一个地区为其人口提供清洁水的能力。并用logistic模型计算了区域的用水状况。本文选择的严重缺水地区是北京，用物理稀缺和经济稀缺结合多年数据和各种可靠的资料解释了为什么存在以及如何解决在这一地区的缺水问题。并用Logistic回归模型结合了环境驱动力等因素分析了北京未来15年的缺水情况，并分析这种情况将如何影响北京公民的生活。

2. 基本方法

2.1. 通过主成分分析法筛选出影响区域最大供水量的主要指标 [1]

用 $x_1,x_2,\cdots ,x_7$ 分别表示：地下水储存量、地表径流、天然降水、水利工程、污水处理回用、海水淡化，水源污染。第i年 $x_1,x_2,\cdots ,x_7$ 的取值分别记为，构造矩阵 $A={\left(a_{ij}\right)}_{5\times 7}$ 。

基于主成分分析法的评价步骤如下：

1) 对原始数据进行标准化处理。将各指标 $a_{ij}$ 转换成标准化指标 ${\tilde{a}}_{ij}$ ，有：

${\tilde{a}}_{ij}=\frac{a_{ij}-{\mu }_j}{s_j}\left(i=1,2,\cdots ,12;j=1,2,\cdots ,7\right)$ (2.1.1)

式中：

${\mu }_j=\frac{1}{12}{\displaystyle \underset{i=1}{\overset{12}{\sum }}{a}_{ij}};s_j=\sqrt{\frac{1}{12-1}}\sqrt{{\displaystyle \underset{i=1}{\overset{12}{\sum }}{\left(a_{ij}-{\mu }_j\right)}^2}},j=1,2,\cdots ,7$ (2.1.2)

即 ${\mu }_j,s_j$ 为第j个指标的样本均值和样本标准差。

对应地，称 ${\tilde{x}}_j=\frac{x_j-{\mu }_j}{s_j},j=1,2,\cdots ,7$ 为标准化指标变量。

2) 计算相关系数矩阵R。相关系数矩阵 $R={\left(r_{ij}\right)}_{7\times 7}$ ，有：

$r_{ij}=\frac{{\displaystyle \underset{k=1}{\overset{12}{\sum }}{\tilde{a}}_{ki}\cdot {\tilde{a}}_{kj}}}{12-1},i,j=1,2,\cdots ,7$ (2.1.3)

式中： $r_{ii}=1;r_{ij}=r_{ji}$ ， $r_{ij}$ 为第i个指标与第j个指标的相关系数。

3) 计算特征值和特征向量。计算相关系数矩阵R的特征值 ${\lambda }_{\text{1}}\ge {\lambda }_{\text{2}}\ge \cdots \ge {\lambda }_{\text{7}}\ge \text{0}$ ，及对应的标准化特征向量 ${\mu }_{\text{1}},{\mu }_{\text{2}},\cdots ,{\mu }_7$ ，其中 $u_j={\left[u_{1j},u_{2j},\cdots ,u_{7j}\right]}^{\text{T}}$ ，由特征向量组成7个新的指标变量

$\begin{array}{l}{y}_1=u_{11}{\tilde{x}}_1+u_{21}{\tilde{x}}_2+\cdots +u_{71}{\tilde{x}}_7,\\ y_2=u_{12}{\tilde{x}}_1+u_{22}{\tilde{x}}_2+\cdots +u_{72}{\tilde{x}}_7,\\ y_5=u_{15}{\tilde{x}}_1+u_{25}{\tilde{x}}_2+\cdots +u_{77}{\tilde{x}}_7,\end{array}$ (2.1.4)

式中： $y_1$ 为第1主成分， $y_2$ 为第2主成分； $\cdots$ ； $y_7$ 为第7主成分。

4) 选择 $p$ ( $p\le 7$ )个主成分，计算综合评价值。

1. 计算特征值 ${\lambda }_j\left(j=1,2,\cdots ,7\right)$ 的信息贡献率和累积贡献率。

称 $b_j=\frac{{\lambda }_j}{{\displaystyle \underset{k=1}{\overset{7}{\sum }}{\lambda }_k}},j=1,2,\cdots ,7$ 为主成分 $y_j$ 的信息贡献率；

称 ${\alpha }_p=\frac{{\displaystyle \underset{k=1}{\overset{p}{\sum }}{\lambda }_k}}{{\displaystyle \underset{k=1}{\overset{7}{\sum }}{\lambda }_k}}$ 为主成分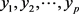的累积贡献率。

当 ${\alpha }_p$ 接近于1( ${\alpha }_p=0.85,0.90,0.95$ )时，则选择前p个指标变量 $y_1,y_2,\cdots ,y_5$ 作为5个主成分，代替原来7个指标变量，从而可对5个主成分进行综合分析。

2. 计算综合得分：

$Z={\displaystyle \underset{j=1}{\overset{\text{p}}{\sum }}{b}_j{y}_j}$ (2.1.5)

式中， $b_j$ 为第j个主成分的信息贡献率，根据综合得分值就可进行评价(表1)。

可以看出，前两个特征根的累计贡献率就达到91%以上，主成分分析效果较好。由此选出地下水储量，地表径流为主要评价指标。

2.2. 用一次线性函数模型计算区域供水能力，并用模糊综合评价法评价， 最后提出投影寻踪模型

2.2.1. 一次线性函数模型计算供水能力

为衡量一个地区为其人口提供清洁水的能力，我们通过主成分分析后得出影响供水量的主要指标：

Table 1. Results of principal component analysis

表1. 主成分分析结果

地下水储存量、地表径流，指标个数的减少方便我们统计该地区的日供水量。我们又统计了该地区的人口数(虽然人口是流动的但总体上波动不大，可视为高阶无穷小量忽略掉)。

(1) 设X为该地区供水量，

(2) 设K为该地区总人口

(3) 设Y为该地区日平均供水量。

每一个X确定一个Y，Y就是X的一次函数

得出：

$Y=X/C$ (2.2.1)

设S为人均用水标准，通过比较设 $K=Y-S$ 的差距大小即可得出该地区为其人口提供清洁水的能力。显然K越大，该地区供水能力越强。

我们把此模型用于北京地区，计算了它的供水能力。

2.2.2. 通过模糊综合评价方法评价现有一次线性函数模型

(一) 评价步骤

1. 取一级评价指标 = {水资源总量、污水排放总量、农业用水量、生活用水，再生水回用量}

取二级评价指标 = {地下水储存量、地表径流、天然降水、水利工程、污水处理回用}

2. 取评语集V = {影响很大 $v_1$ ，影响较大 $v_2$ ，影响一般大 $v_3$ ，影响较小 $v_4$ ，基本无影响 $v_5$ }

3. Delphi法确定权重

4. 确定模糊综合评判矩阵

5. 模糊综合评判

(二) 模型的求解

1. 一级指标权重的确定：

通过Delphi法对一级指标权重进行确定

$A=\left[0.2,0.1,0.2,0.3,0.2\right]$

2. 二级指标权重为

$A_1=\left[0.2,0.15,0.1,0.35,0.2\right]$

$A_2=\left[0.25,0.15,0.2,0.2,0.3\right]$

$A_3=\left[0.1,0.3,0.1,0.25,0.25\right]$

$A_4=\left[0.15,0.25,0.1,0.35,0.15\right]$

$A_5=\left[0.3,0.1,0.2,0.15,0.25\right]$

3. 对各个子因素集进行一级模糊综合评价得到

$B_1=A_1\cdot R=\left[0.28,0.29,0.06,0.37,0.01\right]$

$B_2=A_2\cdot R=\left[0.02,0.165,0.69,0.12,0.37\right]$

$B_3=A_3\cdot R=\left[0.25,0.33,0.125,0.26,0.35\right]$

$B_4=A_4\cdot R=\left[0.25,0.09,0.18,0.35,0.04\right]$

$B_5=A_5\cdot R=\left[0.28,0.14,0.02,0.34,0.07\right]$

这样，二级综合评判为

$\begin{array}{c}C=A\cdot B=\left[0.2,0.1,0.2,0.3,0.2\right]\cdot \left[\begin{array}{ccccc}0.28& 0.29& 0.06& 0.37& 0.01\\ 0.02& 0.165& 0.69& 0.12& 0.37\\ 0.25& 0.33& 0.125& 0.26& 0.35\\ 0.25& 0.09& 0.18& 0.35& 0.04\\ 0.28& 0.14& 0.02& 0.34& 0.07\end{array}\right]\\ =\left[0.2769,0.0685,0.1026,0.1734,0.3481\right]\end{array}$

根据最大隶属度原则，认为该模型不可以很好的衡量北京为其人口提供清洁水的能力。推广后，得出它不能很好的衡量一个地区的供水能力。

2.2.3. 投影寻踪模型 [2]

运用投影寻踪分类法，对区域供水能力进行评价，并与模糊综合评判法结果进行分析比较。

评价指标选取

影响区域供水能力的因素众多，既有供水、需水方面的因素，又有直接 、间接因素，本文根据文献 [3] 选取水资源利用率、缺水率、灌溉率、降水量、人均占水量、径流深、生态用水率7个评价指标，指标的含义如下：

1) 水资源利用率u1：现状75%频率的供水量/水资源总量，%

2) 缺水率u2：现状75% 频率的缺水量/供水量，%。

3) 灌溉率u3：灌溉面积/土地面积，%。

4) 降水量u4：多年平均降水量是区域水资源状况的自然禀赋，mm。

5) 人均占有水量u5：区域水资源总量/总人口，m³/人。

6) 径流深u6：地表径流/流域面积，mm。

7) 生态环境用水率u7：生态用水量/总水量，%。

区域供水能力综合评价因素的分级指标见表2。

Table 2. Grading index of factors for comprehensive evaluation of regional water supply capacity

表2. 区域供水能力综合评价因素的分级指标

由表2供水能力分级指标可知：1级属于状况较差，表示水资源承载能力趋于饱和，会出现短缺，阻碍经济发展；3级属于情况较好，表示流域水资源仍有很大使用空间，其供给情况较为乐观；2级介于两者之间，表明流域水资源已经开发到相当规模，但仍有开发利用潜力，水资源的供给需求在一定程度上能满足区域的社会发展。

我们选取北京为代表又利用模糊综合评价评价了投影寻踪模型，得出它可以很准确的衡量一个地区的供水能力。

2.3. 回归模型 [4]

模拟系列的概率分布一般有MC (蒙特卡罗)、M FOSM (均值一次两阶矩)法、SO (两次矩)法、最大熵风险分析方法、AFOSM (改进一次两阶距)法以及JC法等，这些模拟方法在实际应用时可能会存在一些问题，如对因变量分布的假设过于敏感、计算结果不唯一、模型精度低、收敛性不能得到证明、理论体系不完善等等。而Logistic回归方法具有对因变量数据要求低、计算结果唯一、模型精度高等优点，本文采用Logistic回归模型来模拟缺水量系列的概率分布。

1. 一个自变量的Logistic回归模型可写为：

$\text{Prob}\left(\text{event}\right)=\frac{1}{1+{\text{e}}^{-\left(b_0+b_{1}x\right)}}$ (2.3.1)

式中： $b_0$ 和 $b_1$ 分别为自变量的系数和常数；e为自然对数。包含一个以上自变量的模型可表示为：

$\text{Prob}\left(\text{event}\right)=\frac{1}{1+{\text{e}}^{-x}}$ (2.3.2)

其中：

$Z=b_0+b_1{x}_1+b_2{x}_2+\cdots +b_p{x}_p$ (p为自变量的数量)(2.3.3)

$b_0,b_1,\cdots ,b_p$ 分别为Logistic回归系数。

2. Logistic回归模型拟合度检验和系数检验 建立Logistic回归模型后，常用Hosmer-Losmer 统计量进行模型的拟合度检验，其表达式为

$\text{Chi-square}={\displaystyle {\sum }_1^n{\left(x_s-x_y\right)}^2/x_y}$ (2.3.4)

其中： $x_s$ 和 $x_y$ 分别是实际观测量和预测数量。检验的原假设和备择假设为： $H_0$ 为方程对数据的拟合良好， $H_1$ 为方程对数据的拟合不好。

对于较大样本的系数检验，常用基于 ${\chi }^2$ 分布的Wald统计量进行检验，当自由度为1时，Wald值为变量系数与其标准误差比值的平方，对于两类以上的分类变量来说，其式如下：

$W=B^{\prime }{V}^{-1}B$ (2.3.5)

式中：B为极大似然估计分类变量系数的向量值； $V^{-1}$ 为变量系数渐近方差一协方差矩阵的逆矩阵； $B^{\prime }$ 为B的转置阵。其检验的原假设和备择假设为：H为回归模型的系数等于0， $H_1$ 为回归模型的系数不等于0。

2.4. 模型优缺点分析

2.4.1. 投影寻踪模型优缺点

投影寻踪模型在PPC技术中广泛应用，它的优缺点在PPC技术中得到体现。PPC技术是一种直接由样本数据驱动的探索性数据分析方法，特别适用于分析和处理非线性、非正态高维数据。它的基本思路是：把高维数据通过某种组合投影到低维子空间上，对于投影到的构形，采用投影指标函数来衡量投影暴露某种结构的可能性大小，寻找出使投影指标函数达到最优(即能反映高维数据结构或特征)的投影值，然后根据该投影值来分析高维数据的结构特征。其中，投影指标函数的构造及其优化问题是应用PPC方法能否成功的关键。该问题一般很复杂，传统的PPC实现方法的计算量相当大，在一定程度上限制了PPC方法的深入研究和广泛应用。

2.4.2. 模糊综合评价模型的优缺点

模糊评价通过精确的数字手段处理模糊的评价对象，能对蕴藏信息呈现模糊性的资料作出比较科学、合理、贴近实际的量化评价；而且其评价的结果是一个矢量，而不是一个点值，包含的信息比较丰富，既可以比较准确的刻画被评价对象，又可以进一步加工，得到参考信息。然而其计算复杂，对指标权重矢量的确定主观性较强；当指标集U较大，在权矢量和为1的条件约束下，相对隶属度权系数往往偏小，权矢量与模糊矩阵R不匹配，结果会出现超模糊现象，分辨率很差，无法区分谁的隶属度更高，甚至造成评判失败。

2.4.3. Logistic回归分析预测法优缺点

Logistic回归分析预测法，是在分析现象自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将回归方程作为预测模型，根据自变量在预测期的数量变化来预测因变量关系大多表现为相关关系，因此，回归分析预测法是一种重要的预测方法，当我们在对现象未来发展状况和水平进行预测时，如果能找到影响预测对象的主要因素，并且能够取得其数量资料，就可以采用回归分析预测法进行预测。它是一种具体的、行之有效的、实用价值很高的常用市场预测方法。

3. 说明区域缺水原因

3.1. 综合水资源开发情况选择北京为说明地区

从联合国缺水地图中可明显看出非洲北部，北美南部，欧亚大陆南部，是世界上水资源开发程度较高地区，也就是说，世界主要缺水几区集中在南纬10˚到北纬55˚之间。重合了中国地图对比发现，中国首都北京及其所在华北地区处于严重缺水地区，因此选择北京，华北地区作为典型说明地区(图1和图2)。

3.2. 通过物理和经济短缺解释环境和社会驱动因素 [5]

我们选择中国北京作为解释对象，北京位于华北平原西部，属于暖温带半干旱半湿润性季风气候，由于受季风影响，雨量年际季节分配极不均匀，夏季降水量约占全年的70%以上，全市多年平均降水量575 mm。属海河流域从东到西分布有蓟运河、潮自河、北运河、永定河、大清河五大水系(见图3)。北京是世界上严重缺水的大城市之一，当地自产水资源量仅39.99亿m³，多年平均入境水量16.50亿m³，多年平均出境水量11.60亿m³，当地水资源的人均占有量约300 m³，是世界人均水平的1/30，远远低于国际公认的人均1000 m³的下限，属于重度缺水地区。水资源短缺已成为影响和制约首都社会和经济发展的主要因素(图3)。

北京市水资源开发利用中存在的问题主要有：1) 上游来水衰减趋势十分明显；2) 长期超采地下水导致地下水位下降；3) 水污染加重了水危机；4) 人口膨胀和城市化发展加大了生活用水需求等。因此，导致北京水资源短缺的主要原因有物理缺水和水质型缺水等。影响北京水资源短缺风险的因素可归纳为以下两个方面：1) 物理因素：①人口数；②入境水量；③水资源总量；④地下水位埋深；2) 社会经济环境因素：①污水排放总量；②污水处理率；③COD排放总量；④生活用水量；⑤农业用水量。

Figure 1. WSI (http://www.legrand.com/EN/a-different-vision-of-water-for-legrand-sites_13067.html)

图1. 世界水稀缺指数(http://www.legrand.com/EN/a-different-vision-of-water-for-legrand-sites_13067.html)

Figure 2. Distribution map of water shortage areas in China (http://www.dljs.net/dltp/26365.html)

图2. 中国重点缺水地区分布示意图(http://www.dljs.net/dltp/26365.html)

Figure 3. Beijing river system (from Baidu Baike)

图3. 北京水系(来源自百度百科)

Figure 4. Total agricultural using water (100 million cubic meters)

图4. 农业用水总量(1亿立方米)

Figure 5. EIW

图5. EIW

Figure 6. Total water (100 million cubic meters)

图6. 用水总量(1亿立方米)

Figure 7. Water supply capacity

图7. 供水能力

Figure 8. Gross regional product (100 million yuan)

图8. 地区生产总值(1亿元)

Figure 9. Total resources (100 million cubic meters)

图9. 水资源总量(1亿立方米)

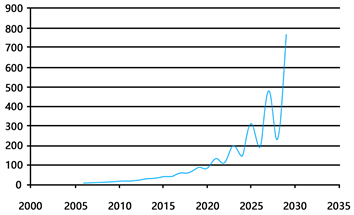
Figure 10. Total using water (100 million cubic meters)

图10. 生态用水总量(1亿立方米)

Figure 11. Total using water (100 million cubic meters)

图11. 生活用水总量(1亿立方米)

北京市水资源短缺的空间分布性说明城市化的扩张加剧了水资源短缺的程度。人口数量越多，经济发展程度越大的地区水资源短缺程度越大(如北运河流域和大清河流域)。需要对北京市各个流域进行针对性的管理，以缓解北京市整体的水资源短缺状况。

最后，我们又利用logistic回归计算出了缺水发生的概率，水资源短缺风险值是由基于模糊概率的水资源短缺风险评价模型计算出来的，并且得到：资源总量、污水排放总量、农业用水量、生活用水是影响北京地区水资源短缺风险的敏感因子。水资源总量、污水排放总量、农业用水量以及生活用水量是北京市水资源短缺的主要致险因子；再生水回用和南水北调工程可使北京地区2010~2020年各类规划水平年的水资源短缺均降至低风险水平。所以，在加快南水北调进京工程的同时，大力发展再生水回用，是解决北京地区水资源短缺风险的根本措施。

3.3. 用logistic模型展示北京未来15年水状况

利用logistic模型模拟出北京未来15年影响水状况的相关因素的变化趋势：如图4~图11。

基金项目

本文得到内蒙古大学自治区级大学生创新创业训练项目支持，项目编号(201610126059)。

[1] Hashimoto, T., Stedinger, J.R. and Loueks, D.P. (1982) Reliability, Resiliency and Vulnerability Criteria for Water Resources System per formance Evaluation. Water Resources Research, 18, 14-20. https://doi.org/10.1029/WR018i001p00014

[2] 李建明, 谌黔鸣. n维空间中可连续变化的标准正交基的构造与投影追踪[J]. 贵州工学院学报, 1996(6): 24-28.

[3] 裴丽萍. 水资源市场配置法律制度研究——一个以水资源利用为中心的水权制度构想[M]//环境资源法论丛第一卷, 北京: 法律出版社, 2001: 131.

[4] Bagel, M.S., Das Gupta, A. and Nayak, D.K. (2005) Amodelfor Optimal Allocati on of Water to Competing Demands. Water Resources Management, 19.

[5] National Agricultural Commission. Technical Specification for Land Use Survey. Publishing House of Surveying and Mapping, Beijing, 1984.