1. 引言
石油的不可再生性、环境恶化等因素限制了传统汽车的发展,世界主要汽车大国都在致力于电动汽车的研究 [1] 。电动汽车的关键技术之一是动力电池,它的性能及成本直接决定了电动汽车的发展前景。当前主流的锂离子电池的封装形式主要有三种:圆柱、方形、软包。相比于方形和软包电池,圆柱形锂离子电池作为电动汽车动力电池有三大优势:标准化程度高、生产工艺成熟;PACK成本较低、易于替换;产品一致性较高。而其劣势在于散热性能逊于方型和软包电池。因此,优化圆柱形电池的热性能一直是学术及产业界研究和关注的焦点。
在锂离子电池充放电过程中有复杂电化学反应和物理变化,产生的大量热量,若热量积聚会导致电池温度过高。温度对电池的安全性、使用性能和寿命影响显著。高温不仅诱发内部材料降解进而损害和降低电池的性能和寿命,还可能引起动力电池热失控,造成车辆和乘客的安全事故。文献 [2] 从表面对流系数、外壳导热系数和厚度对MH-Ni方形动力电池散热分析;文献 [3] 利用COMSOL Multiphysics对18650锂离子动力电池模块定量分析不同工作电流条件下的温度分布。
影响电池热性能的因素多种多样,除了外界环境还包括电池结构及材料构成。因此全面、系统地研究以18650为代表的圆柱状锂离子电池的热性能十分必要。
2. 建立圆柱形锂离子电池电化学-热耦合模型
2.1. 锂离子电池电化学模型原理
锂离子电池电化学模型是Newman及其同事在上世纪90年代建立的多孔电极理论的锂离子电池数学模型,该模型作了一些假设,忽略锂离子电池内部的副反应,将活性物质粒子假设为大小单一球形颗粒,锂离子的嵌入和脱出发生在活性材料表面 [4] [5] [6] 。
根据菲克第二定律,用式(1)描述正负电极固相活性材料中锂离子的扩散和迁移,边界条件式(2)内部中心浓度变化梯度的为零,反应离子电流用公式(3)表示。
 (1)
(1)
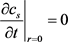 (2)
(2)
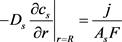 (3)
(3)
式中Ds、r、Cs、t、As、J、F分别是锂离子在球形活性材料粒子内的扩散系数、粒子的半径、固相锂离子浓度、锂离子嵌入或脱出反应时间、活性物质颗粒表面面积、嵌入和脱嵌反应电流、法拉第常数。
依照欧姆定律,式(4)阐述固相电势分布变化。
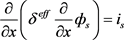 (4)
(4)
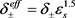 (5)
(5)
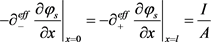 (6)
(6)
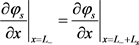 (7)
(7)
在电极和集流体界面的固相电子电流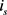 与外部应用电流I相等,电子无法自由通过隔膜导致电极和隔膜界面电子电流为零。多孔电极的导电率,服从Bruggeman修正,
与外部应用电流I相等,电子无法自由通过隔膜导致电极和隔膜界面电子电流为零。多孔电极的导电率,服从Bruggeman修正, 、
、 和
和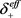 、
、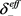 为正负极固相活性物质的电导率和有效导电率,
为正负极固相活性物质的电导率和有效导电率,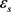 为活性物质体质体积分数,
为活性物质体质体积分数, 为负极厚度,
为负极厚度,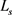 为隔膜厚度。
为隔膜厚度。
活性材料粒子与电解液接触的表面发生电荷转移,该过程采用Bulter-Volmer方程描述:
 (8)
(8)
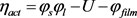 (9)
(9)
 (10)
(10)
式中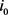 电极反应交换电流密度,
电极反应交换电流密度,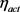 电极动力学过电势,
电极动力学过电势,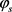 为固相活性物质电势,
为固相活性物质电势, 为电解液液相电势,U开路电势,
为电解液液相电势,U开路电势,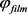 为SEI膜电势,
为SEI膜电势, 和
和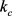 为正负极反应常数,
为正负极反应常数,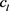 电解液锂离子浓度,
电解液锂离子浓度,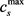 为表示正负极活性物质最大嵌入锂离子浓度,
为表示正负极活性物质最大嵌入锂离子浓度, 为活性材料粒子表面浓度,
为活性材料粒子表面浓度, 电解液锂离子参考浓度。
电解液锂离子参考浓度。
电解液中锂离子满足质量守恒控制方程:
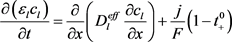 (11)
(11)
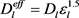 (12)
(12)
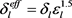 (13)
(13)
由于锂离子在多孔电极电解液内曲折迁移,采用Bruggman理论对液相动力学传输性能参数离子电导率和电解液扩散系数进行修正,其中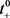 为锂离子迁移数,
为锂离子迁移数,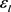 为电解液体积分数,
为电解液体积分数,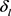 为电解液导电率,
为电解液导电率,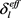 为电解液有效电导率。
为电解液有效电导率。
正负电极内电解液与集流体接触界面的浓度梯度为零,因此边界条件为:
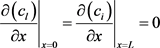 (14)
(14)
电解液电势变化一部是由于电解液的离子电阻导致的电解液相欧姆电压降,另一部分是由于由锂离子在电解液中的浓度分布不均匀而引起的浓差极化过电势。
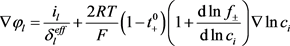 (15)
(15)
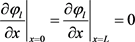 (16)
(16)
由于锂离子只能在电极和隔膜中迁移,因此集流体与电极的界面电解液中离子电流下降至零。其中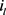 为液相电流,由于锂离子电池内部服从电荷守恒,因此液相离子电流与固相相电流的和应等于外部负载电流。
为液相电流,由于锂离子电池内部服从电荷守恒,因此液相离子电流与固相相电流的和应等于外部负载电流。
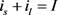 (17)
(17)
2.2. 锂离子电池热模型原理
锂离子电池生热量包括副反应热、反应热、极化热和焦耳热。过充和过放、电解质分解及自放电产生的副反应热 几乎为零 [7] 。只用考虑剩下的三部分热量,反应热
几乎为零 [7] 。只用考虑剩下的三部分热量,反应热 :在进行充放电时,锂离子和电子发生嵌入和脱嵌,运动过程中产生热量如式(18),两者遵循电荷守恒定律。
:在进行充放电时,锂离子和电子发生嵌入和脱嵌,运动过程中产生热量如式(18),两者遵循电荷守恒定律。
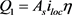 (18)
(18)
在电池的可逆反应中,理论上反应热大小相等、符号相反,但根据熵增原理,在实际进行充放电时会有极化反应产生的极化热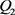 。如式(19):
。如式(19):
 (19)
(19)
在充放电过程中电池内阻产生的焦耳热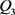 ,分为固相电子电阻和液相离子电阻产生固相欧姆热和液相欧姆热。
,分为固相电子电阻和液相离子电阻产生固相欧姆热和液相欧姆热。
 (20)
(20)
锂离子电池的总热量记为Q,可表示为:
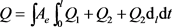 (21)
(21)
其中 为活化比面积、
为活化比面积、 为局部电流密度、h过电势、U为开路电压、T为电池温度。
为局部电流密度、h过电势、U为开路电压、T为电池温度。
对于圆柱型锂离子电池,在极坐标下建立数值模型方程 [8]
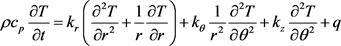 (22)
(22)
 、
、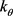 、
、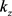 分别为圆柱型锂离子电池r、θ、z向导热率,r和
分别为圆柱型锂离子电池r、θ、z向导热率,r和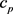 为电池的密度和比热容,q为圆柱型锂离子电池单位体积产热率。
为电池的密度和比热容,q为圆柱型锂离子电池单位体积产热率。
根据牛顿冷却定律,锂离子电池热模型的边界条件用式(23)来描述 [9] :
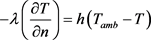 (23)
(23)
Tamb为周围流体的温度,T为电池表面温度,l为电池外壳的导热系数,n表示电池径向矢量,h为电池表面与周围流体间的对流传热系数。
2.3. 锂离子电池热物理参数确定
由于电池各成分的材料热物理性参数比较复杂,铜、铝、钢等单一材料的热物理参数可通过手册查的 [10] 。正极材料、隔膜等成分较为复杂,其物理参数通过文献查找得到 [11] [12] 。为了提高模型的实用性和收敛速度,对电池的比热容、密度以及导热系数进行均一化处理。根据文献,一般使用各层材料加权平均的方法获得 [11] [13] 。标准试验系统结果数据NCA锂离子电池各部分材料,如表1所示;
内部活性物质的平均密度为各部分材料密度与厚度乘积除以电池总的厚度:
 (24)
(24)
锂离子电池的平均比热容可以通过式(25)计算:
 (25)
(25)
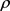 和
和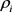 分别为电池的密度、各种材料的密度;
分别为电池的密度、各种材料的密度;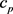 和
和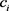 分别为电池的比热容、各种材料的比热容;
分别为电池的比热容、各种材料的比热容;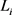 为18650锂电池中各种材料的厚度。
为18650锂电池中各种材料的厚度。
圆柱型电池里面是正负电极层和隔膜绕着轴心卷绕,因此电池内部径向和轴向导热系数存在各向异性,可通过计算得到。根据传热学的基本原理,(26)和(27)式用于计算串联和并联材料的导热系数:
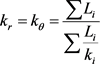 (26)
(26)
 (27)
(27)
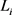 和
和 分别为18650锂离子电池中各材料的厚度和导热系数。活性区域的密度、比热容计算为2523 kg/m3,1145 J/(kg∙K),导热率径向导热率和轴向导热率计算分别为1.2 W/(m∙K)和34.4 W/(m∙K)。
分别为18650锂离子电池中各材料的厚度和导热系数。活性区域的密度、比热容计算为2523 kg/m3,1145 J/(kg∙K),导热率径向导热率和轴向导热率计算分别为1.2 W/(m∙K)和34.4 W/(m∙K)。
2.4. 锂离子电池热物理参数确定
用COMSOL Multiphysics在Newman理论下开发了电池与燃料电池模块构建一维电化学模型和运用固体传热模块构建锂离子的传热和散热模型,共同组成了2.2 Ah 18650锂离子电池电化学-热耦合模型。一维电化学模型主要包含正负极电极、正负极集流体和隔膜,由于圆柱型锂电池是旋转轴对称的几何结构,为了使模型计算简便建立二维旋转模型。模型参数,如表2所示。
3. 实验
选用松下的18650三元锂电池为研究对象,由钢壳、电芯、集流体和极耳构成,电芯包括正极材料、隔膜、负极材料和电解液,基本参数见表3。
电池性能试验使用设备为武汉市蓝电股份有限公司产CT2001B多通道电池测试系统,对实验电池进行恒流放电;电池测试系统辅助温度通道用于监测电池表面温度,监测传感器为T型热电偶;恒温箱为实验电池提供稳定的环境温度。
在25℃恒温箱环境下,锂离子电池先采用0.2C (0.44 A)恒定电流充至4.2 V后再恒定电压充电至截止电流0.04C (88 mA),然后静置4小时,分别采用0.5C (1.1 A),1C (2.2 A),1.5C (3.3 A)和2C (4.4 A)的将锂离子电池由充满放电至截止电压2.75 V。记录电池的电压和温度变化。

Table 1. Thermo physical parameters of various parts of NCA lithium ion batteries
表1. 标准试验系统结果数据NCA锂离子电池各部分材料

Table 3. Basic parameters of three yuan lithium ion battery monomer
表3. 三元锂离子电池单体基本参数
4. 结果与讨论
本文主要从放电倍率、环境温度、散热介质及流动形态、电极厚度四个方面分析锂离子电池热性能。
4.1. 放电倍率的影响
外界条件设置环境温度为25℃、h为5 W/m2∙K,其它参数设置参考上面。利用COMSOL Multiphysics 5.3平台计算锂离子电池在不同放电倍率:0.5C、1C、1.5C、2C,放电结束时电池温度情况。
图1是锂电池25℃环境下由满电荷状态分别以0.5C、1C、1.5C和2C恒定电流放电至截止电压2.75 V时的温度图,电池表面平均温升分别为2.84℃、7.8℃、13.68℃和19.77℃。电池内部最高温升和表面平均温升随着电池的放电倍率增大而提高,电池内外温度差也随着电池放电倍率的提高而增大,分别是0.05℃、0.13℃、0.22℃、0.32℃。
图2对比验证0.5C、1C、1.5C和2C的放电升温特性,实线为在仿真计算18650锂离子电池在25℃
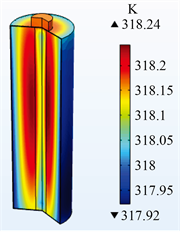
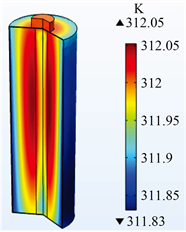
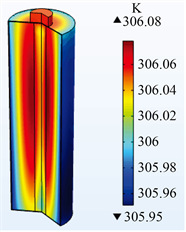
 (a) 0.5C放电结束时电池温度 (b) 1C放电结束时电池温度 (c) 1.5C放电结束时电池温度 (d) 2C放电结束时电池温度
(a) 0.5C放电结束时电池温度 (b) 1C放电结束时电池温度 (c) 1.5C放电结束时电池温度 (d) 2C放电结束时电池温度
Figure 1. Battery temperature at the end of 0.5C, 1C, 1.5C and 2C discharge
图1. 0.5C、1C、1.5C、2C放电结束时电池温度
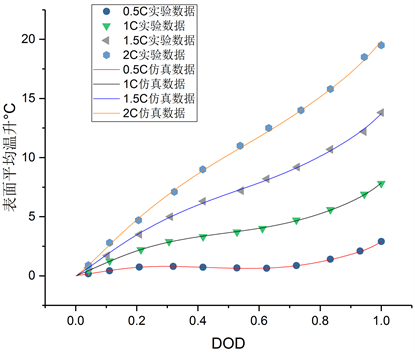
Figure 2. Experimental data and simulation data
图2. 实验数据与仿真数据
环境下由满电荷状态别以0.5C、1C、1.5C和2C恒定电流放电至截止电压的过程中电池表面平均温升数据,点为T型电偶紧贴电池表面记录的表面平均温升。试验结果和仿真结果具有良好一致变化规律且差异较小,仿真和试验结果的温度差值±0.5℃范围内。表明该电化学-热耦合模型具有较高的精准性,可以预测电池热特性。
4.2. 环境温度的影响
不改变其他边界条件,参数设置一样,定量分析环境温度对电池散热的影响。在模型中分别设置电池工作环境温度为−10℃、0℃、10℃、25℃和40℃进行1C放电仿真计算,提取内部最高温升数据进行比对分析。
数据所得图3,环境温度较低时温升相比环境温度较高时要高,上升速率也要快。电池工作温度为−10℃、0℃、25℃、40℃时,放电结束时内部最高温升分别为11.67℃、10℃、7.93℃、7.24℃,对应的电池内部最高温度分别为1.67℃、10℃、32.93℃、47.24℃。研究表明,锂离子电池的最佳工作温度范围
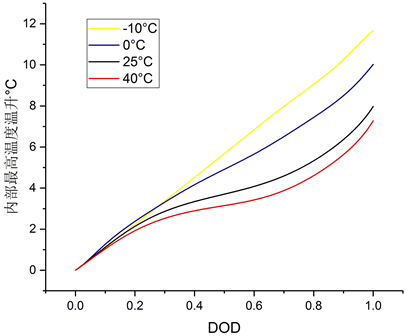
Figure 3. Maximum temperature rise curve under different ambient temperatures
图3. 不同环境温度下最高温升曲线
为25℃~40℃,电池之间的温差应低于5℃ [14] ,而且低温情况下电池以1C放电时间不到3600 s,−10℃才放电到2854 s,0℃放电到3327 s,这是由于低温时电池反应阻力大,影响电池性能。
4.3. 散热介质及流动形态的影响
根据表4选择几个具有代表性的对流表面系数,选取h为5、10、25、50、100 W/m2∙K五个典型值进行仿真计算,分析对流表面系数对电池热性能的影响。
h为5、10、20、50、100、1000时对应的放电结束时表面平均温升为7.81℃、5.41℃、3.43℃、1.67℃、0.91℃、0.09℃ (见图4)。结果表明表面对流系数是电池散热的主要影响因素,由5到100温升下降了5.14℃,而100到1000只下降了1.58℃。强制风冷对电池散热是比较有效而且经济性较高的方式。并且仿真计算数据中显示电池内部最高温升和表面温升差值分别为0.12℃、0.17℃、0.22℃、0.26℃、0.29℃、0.29℃同时表明,电池表面对流传热系数h越大,电池的温差也随之变高,但是越到后面变化幅度越小,这对电池包散热方式选择具有参考意义。
4.4. 电极厚度的影响
电极厚度与电池能量密度有着直接关系,其他条件不变电极越厚载入的活性物质越多,容量也就越高。对于电极层层缠绕因而散热面积较小的圆柱型电池,电极厚度需要在一个合理的区间,对电极厚度定量来分析对电池热性能的影响。
锂离子电池的容量由活性物质的载入量决定,对于锂离子电池的容量可根据公式(28)确定
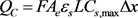 (28)
(28)
其中 为电极面积,F为法拉第常数,
为电极面积,F为法拉第常数,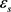 为活性物质体积分数,
为活性物质体积分数,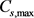 为电极最大嵌入锂离子浓度,L为电极厚度,
为电极最大嵌入锂离子浓度,L为电极厚度,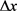 为锂离子浓度变化范围。在其他变量不改变的情况下只改变电极厚度,对应的容量也会相应的变化如下表5所示。
为锂离子浓度变化范围。在其他变量不改变的情况下只改变电极厚度,对应的容量也会相应的变化如下表5所示。
图5为不同电极厚度的18650锂离子电池在环境温度设置为25℃、热边界条件表面对流系数h设置为5 W/(m2∙K)时,1C放电曲线。由图可知电极厚度51.12~47.60 μm变化到83.06~77.34 μm,对应的容量
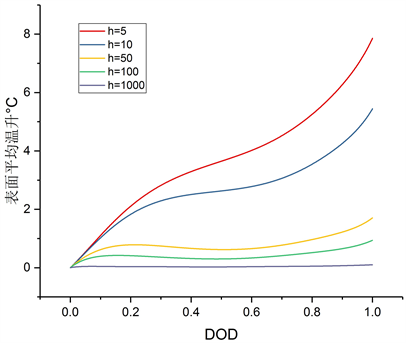
Figure 4. Internal and external temperature rise curves under different surface convection coefficient
图4. 不同表面对流系数下内外温升曲线
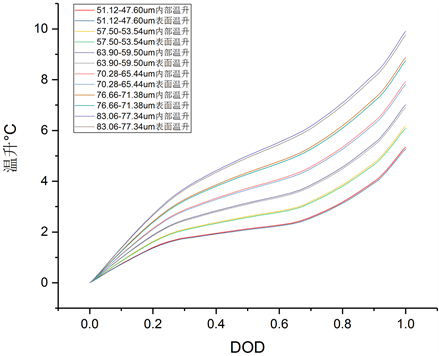
Figure 5. Inside and outside temperature rise curve of different electrode thickness
图5. 不同电极厚度时内外温升曲线

Table 4. Different convective surface coefficients
表4. 不同对流表面系数

Table 5. Relationship between electrode thickness and capacity change
表5. 电极厚度与容量变化关系
由1.6 Ah增加到2.6 Ah,放电结束时表面平均温升分别为5.27℃、6.08℃、6.91℃、7.81℃、8.74℃、9.76℃,每增加0.2 Ah,表面平均温升分别提高0.81℃、0.83℃、0.9℃、0.93℃、1.02℃。电池内外温差分别是0.08℃、0.09℃、0.1℃、0.12℃、0.13℃、0.14℃。结果表明电极厚度一定比例增加电池容量也对应比例增加,结束表面温升上升地会越来越大,但是基本呈线性,单体电池内外温差也越来越大。
5. 总结
1) 在已知电池热物理参数情况下,利用COMSOL Multiphysics仿真软件建立电化学–热模型来进行定量分析,可以方便准确地研究电池散热因素,对电池结构设计和生产具有指导意义。
2) 电池放电倍率和电池表面对流传热系数对圆柱型锂离子电池温度影响明显,正常情况时应该保持在1C内放电,高倍率放电时应该通过强制风冷或者水冷等方式来提高电池表面对流系数的加强热。
3) 电池工作环境温度对电池表面温升有一定的影响,低温时温升较快。当电动车在不同环境下工作时,电池温度需要实时监测,低温时需要进行加温。
4) 18650锂离子电池电极厚度增加,使得容量从1.6 Ah到2.6 Ah每增加0.2 Ah电池表面平均温升提升0.8℃~1℃。