1. 引言
人类在生产实践和科学实验中,逐渐认识了化学、形成了化学学科。
化学的根本问题是化学键,即原子之间是怎样产生结合力的,这结合力的本质是什么?
1.1. 《化学键的本质》是化学键认识的一个历史总结
美国科学家Pauling 1938年出版《化学键的本质》 [1] (第三版1960年),总结了此前百多年化学键的研究成果,特别是上世纪30年代量子化学早期用于化学键研究的成果,奠定了化学键本质研究的基础。关于化学键认识的历史,Pauling在晚年曾写文章 [2] 进行过总结,另有大量的综述 [3] [4] [5] [6] [7] 。
《化学键的本质》将化学键定义为:就两个原子或原子团而言,如果作用于它们之间的力能够导致聚集体的形成,这个聚集体的稳定性又是大到可让化学家方便地作为一个独立的分子品种来看待,则我们说在这些原子或原子团之间存在着化学键。简单地说,化学键是指分子内部原子之间的结合力,这个定义是对客观化学事实的抽象概括,它没有涉及化学键本身的机制,至今仍是适用的。
《化学键的本质》将化学键按其性质作的分门别类,至今仍然是化学常识。现在化学键按成键机制大体被分为:共价键、离子键和金属键。还有和这些键的机制不一样的,为另类:氢键、范德华作用。
事到如今,又半个多世纪过去了,Pauling所定下的化学键定义和分门别类的格局还没有原则性的变化。
人类认识客观世界,总是从个别到一般,又从一般到个别的。化学实践和化学键的认识也是这样。先一一认识个别的化学实体、化学键,然后发现它们的共性,归纳成一般的概括、概念。相同性质的化学键归为一类,认为不能在同一类的则另类,从而分门别类。
共价键。定义是两个原子通过共用电子对产生的吸引作用,典型的共价键是两个原子吸引一对成键电子。这实质是一种核(或基团、原子团)之间的电子共享。形成共价键的多为非金属元素。例如,两个氢核同时吸引一对电子,形成稳定的氢分子。还有极性共价键、配位键也属于此种。
离子键。定义是两个原子间的电负性相差极大时,形成阳离子和阴离子,它们通过静电作用相互吸引而成键。一般是金属与非金属之间的成键。
金属键。这是金属原子结合在一起时,金属离子被固定在晶格结点上,处于离域电子的“海洋”之中,电子可以在核之间自由流动。
氢键。被列入另类,定义是在分子中失去电子较多的带正电荷的H,同时靠静电吸引两个电负性高带有负电荷原子。
范德华作用。也被列入另类。是电子已经配对的原子或分子之间形成的微弱引力。它被认为是三种力的作用:静电力、诱导力、色散力。这些更加不同于上面的各种类型。
在化学键认识的历史中,由个别到一般,这种对化学键的分门别类,再由一般到个别,去认识更多的个别化学实体,历来大大地促进了对化学键的认识,形成了丰厚的化学键知识系统。
1.2. 各种化学键从Hellman-Feynman静电定理的视角看有着统一的本质
人类认识还有这样的规律,即看似分门别类纷繁复杂的不同事物,如果能找到它们共同平易的本质,就是认识的更高一层,是认识的升华。
化学实践和化学实验新发现的化学结合作用,用现有的分门别类并不能完全包容。比如
,并没有配对电子,是一个单电子键。在氢键通式X―H…Y中,发现了弯曲氢键,且是Y与X直接有氢键相关,而不是H与Y之间。还有费解的蓝移氢键。氢键和范德华作用与共价键在本质上还完全不一样。这些事实要求化学键概念需要深入变化和发展,看化学结合力、化学键是否有一个统一的机制和概念。
然而,经典的分门别类的化学键、化学作用,它们之间对其本质的解说差别是那么大,是不那么能够弥合、统一的,那些根深蒂固的定义、概念反而成为化学键进一步研究、统一的障碍。
在前文 [8] 我曾经引用过Hellman-Feynman静电定理,它实际上给出了化学结合力、化学键的物理本质:原子(或基团)对成键区的电子共享产生了结合力。这结合力对抗了体系中电子之间、核之间的斥力,达到各种程度的稳定平衡,形成了化学键。
现在可以根据Hellman-Feynman静电定理来考察分门别类的化学键、化学作用,不只是从它们已有的定义、概念出发,而是从形成化学键、化学作用前后的分子轨道MO和电子密度差Δρ的具体图像和数值,观察它们是怎样在实现原子(或基团)对成键区的电子共享产生结合力的。
其实,共价键本来就是电子共享,它是电子共享的最基本形式。所有的计算都表明如此。而且用电子共享这个概念,把单电子自然也包含进来了,不用专门说共价键是配对电子。前文 [8] 已经专题讨论过共价键了。
金属键本就公认是“高度离域的共价键”,自然也是电子共享,是无数的核在无数的电子海洋之中,是这样一种电子共享。
关键是离子键,它历来被认定是正负离子之间靠静电作用相互吸引而成键,不认为也是一种电子共享。比如Li-F,由于二者电负性差距极大,成键后电子主要跑到F上去了,成为正负离子。这其实只是想当然,实际上,如果用现在精细的量子化学计算,Li有0.6568个电子转移到F上了,它可以认为是强极性共价键,也属于电子共享。离子键所构成的离子晶体呢,它们真的成为正负离子了吗?本文专题讨论离子键和离子晶体的问题。
1.3. 本文的一些约定
本工作用Gaussian16程序 [9] 进行量子化学计算,各种计算方法(选择收敛好的)会在文中说明,而基组统一用6-311++G**。另外的基组则在文中说明。进一步用Multiwfn 3.1 [10] 进行数据处理和作图。
作电子密度差Δρ时,原子ρ的数据取自Multiwfn程序自带的球对称化原子波函数文件。等值线起始值为±0.0004,用几何级数来生成等值线,步长为2,设定等值线条数为10。虚线为ρ减少的区域,实线为ρ增加的区域。此外的数值则在文中说明。距离不标出单位时是Å,电荷和能量数值不标出单位时是a.u.
2. 离子键与离子晶体
长期以来,基于实验结构测定的晶体(含离子晶体)研究,得到长足的发展,总结出了晶体的各层次的规律性和理论解释,形成丰富完整的晶体学科体系[1, 11],促进了晶体材料的科学研究和应用。
本节则是从分子轨道MO和电子密度差Δρ的具体图像和数据,根据Hellman-Feynman静电定理来考察离子键和离子晶体在共享成键区电子时的具体情形。
2.1. 离子键
离子键被认为是两个原子间的电负性相差极大时,电子转移会形成阳离子、阴离子,它们通过正负电荷的静电作用相互吸引而成键,形成离子键和离子键晶体。一般是金属与非金属之间成键。这与上面电子共享的共价键在本质、机理上似乎并不相同、不相容,它阻碍了化学键概念的统一。
在前文讨论极性共价键时,转移电子主要进入了反键区,并不会形成因正负电荷静电吸引对成键作贡献。可以对离子键、离子晶体具体计算一下,看看实际情况到底如何。即离子性可以到什么程度呢?真是离子的相互静电吸引吗?所谓离子键、离子晶体是怎样共享电子的?
既然因电子转移形成了离子,那么就应该以电子转移的量来衡量键的离子性。即如果转移了0.5个电子,就说它有50%的离子性。转移了1个电子,就说它有100%的离子性,此时形成了正负离子。至于对电荷转移量的计算,本文采用分子与组成它的原子的电子密度差Dρ来求得,Dρ中的增加量就是转移的电子量,并可以用盆积分 [10] 的方法对其精确定量。Dρ求得的电荷在原子上的转移量,就是原子的净电荷,也是定量离子性的数据依据。
本文用ωB97XD [12] 方法计算。
首先看看Li-F这个具有代表性离子键分子的电子结构。经过优化,键长为1.5784(手册 [13] 气相分子为:1.51±0.08)。这里,据电荷分布计算的键长与实测符合,支持了电荷分布的合理性。在作离子键、离子晶体的Δρ时,原子的电子密度通过Multiwfn自带的球对称化的原子波函数获得,避免了分子中原子基函数在不同取向下Δρ作图结果不同的问题。
Li-F分子可以看作是Li的单电子和F的单电子形成的化学键,并形成了Li-F分子的一个MO4,见图1(A),虚实线是MO的相位。在这个分子里,对照分子轨道基函数系数看,Li的那个单电子受F的强力吸引大大向F变形、极化了,Li还采用了能向前延伸、转移的p型基函数,可以看作是广义的sp杂化。
这MO4(即σ键)与Li的单电子轨道和F的那个单电子轨道作电子密度差Δρ等值线图,见图1(B),正负值为电子密度的增减量。这里只是对相应的轨道作Δρ。如果作全电子的Δρ,F上的孤对电子虽然与分子的成键轨道MO4是正交的、不参与成键,但是Li-F的键电子与孤对电子的排斥和大量转移电子过来会使孤对电子发生形变,杂在Δρ图中会影响对键电子图像的识别、分析、定量。
这个Δρ图1(B)可以清晰地看到自由的Li、F原子结合成Li-F分子后电子密度ρ的变化。Li大量的电子转移到F上了,计算的电荷转移量为0.6568。这个是总的电荷转移量,就是此时的原子净电荷,用以判断离子性的大小,即66%的离子性,这里没有区分成键区和反键区的电子。Pauling的《化学键的本质》当年根据实际经验计算判断它在气体时具有94%的离子性。
从图1(B)可以看到,Li、F之间有电子在成键区增加,是成键的共享电子的增加。同时,在F的背后也有转移电子在显著增加,这些转移电子恰恰勾画出了与反键区相同的区划,这部分电子是反键性质

Figure 1. (A) MO4 in LiF; (B) Δρ in LiF; (C) crystal in (LiF)18; (D) Δρ in (LiF)2
图1. (A) LiF的MO4;(B) LiF的Δρ;(C) (LiF)18的晶体;(D) (LiF)2的Δρ
的 [8] 。可见不能简单地将双方的成键看作是因电子转移形成的正负电荷的静电吸引作用。转移电子并不都增加到成键区,那样成键区电子的密度会过高、排斥会过大。电子排斥使得过量的电子安排在反键区了,具有反键性质。这是极性键、强极性键,乃至所谓离子键共同的情况,这种情况否定了离子键是正负离子吸引的理论设想。离子键同样也只是对成键区的电子共享。
图1(B)还可以看到,转移走了大量电子的Li核后面也有少量的增值,这是Li转移走电子后电负性增大余下电子收缩密度增加的结果。
2.2. 离子晶体
离子键构成的LiF离子晶体,它属于NaCl型正立方体晶体,见图1(C)。LiF晶体中F上净增加的电子就是晶体中Li向F转移的电子,也即此时原子净电荷。转移电子的量正是判断键的离子性的依据。
取晶体中的一个Li-F来计算,与晶体中的键长一致,晶体中Li-F实测键长为2.01(手册 [13] :2.009)。从它的Δρ得到单个的Li-F中Li向F转移了0.7002个电子,即计算有70%的离子性。
再取晶体中的两个Li-F来计算,即算(LiF)2,它的全电子Δρ的等值线图见图1(D)。它是由两个LiF组成一个晶面的正四边形,键长、键角取晶体中的。这里一个Li与两个F相连成键,一个F与两个Li相连成键。值得注意的是,当用Multiwfn来计算晶体的Δρ中一个指定的F原子上新增的电荷量时,需要精确指定计算原子上净增电荷的空间。这空间,F与F之间有一个交界,越过交界就把对方的电荷也划入了,这交界就是F与F距离的一半。(LiF)2中一个F上的电荷净增量为0.5674。从图中的正负区看,负值区中也有一点正的值,但在对指定F的一个特定空间作电荷盆积分时正负值是分别加和的,并不会涉及Li处的微小正值。何况通过Multiwfn“盆积分”细算这小空间的电子量为±0.0025,可以忽略。
既然Li-F有大量的电子转移,在LiF晶体中,一个Li周围围绕着6个电负性大的F,想来且不是Li要真正成为正离子?同时,F周围有6个电负性小的Li,且不是F要真正成为负离子?
图1(C),画出了LiF立方晶体一块微晶(LiF)18的一个立方晶格图,晶体中的LiF的键长取实测值2.01。微晶(LiF)18包含了6配位的Li和6配位的F,而且在面、棱、角上还有5、4、3配位的F。它上下共三层,图2(A)是中层截面的Δρ的等值线图,此层共有12个原子。
需要说明的是:从微晶(LiF)18的Δρ的正负电荷增值看,F处的转移电荷比较集中,而Li周围的减少电荷则比较发散,作盆积分时,正值区的计量易于充分一些,电子转移量只计算正值电荷即可,得失的电荷正负值的绝对值是相等的。
算(LiF)18,求得它对各原子的电子密度差Δρ。这里,可以找到与Li相连成键的各种F,用Multiwfn程序对这各种F在指定的空间范围进行盆积分,得到该原子上的电荷净增加量如下(1、2是上面单独算出的):
与1个Li相连成键的F上的电荷转移量为0.7002。
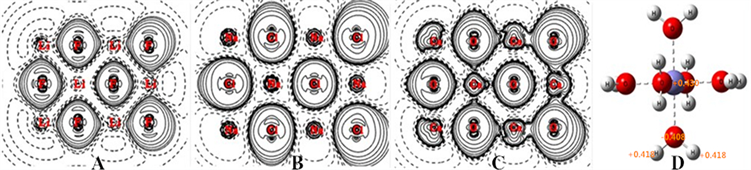
Figure 2. (A) Δρ in (LiF)18; (B) Δρ in (NaCl)18; (C) Δρ in (CaO)18; (D) atomic charges in [Fe(H2O)6]3+
图2. (A) (LiF)18的Δρ;(B) (NaCl)18的Δρ;(C) (CaO)18的Δρ;(D) [Fe(H2O)6]3+的原子净电荷
与2个Li相连成键的F上的电荷转移量为0.5674。
与3个Li相连成键的F上的电荷转移量为0.4543。
与4个Li相连成键的F上的电荷转移量为0.3746。
与5个Li相连成键的F上的电荷转移量为0.3243。
与6个Li相连成键的F上的电荷转移量为0.2602。
6配位是该晶体内的实际情况,而且这是6个键同时转移电子的总量,是原子净电荷,单个键的转移量为0.0433。
这里虽然对一个微晶的面、边、角算出了各种相连数(或说配位数)的F原子电荷聚集情况,但是对实际晶体,6连接才是该晶体基本形式。可以看到,随着F与Li的连接数目增多,F上从Li转移过来的电荷量却显著减少。同样随着Li与的F连接数目增多,Li上电荷转移走的量也显著减少。总的说来就是LiF晶体的离子性反而大大减小了!出乎意料,为什么会是这样?
对于一个客观存在的Li-F键,既可以看作是具有一个价电子的Li和具有一个价电子的F电子配对结合成键的,又可以看作是负离子F-1向正离子Li+1产生配位结合成键的。可以从这两种情况来分析一下。
在Li和F之间成键时,电负性大的F原子参加成键的轨道得到部分电子,电子对核的屏蔽增强,使其电负性降低,电负性小的Li原子失去部分电子,电子对核屏蔽减弱,其电负性升高,当得失电子使双方电负性均衡,便不再有电子流动,此时符合电负性均衡原理。
当在(LiF)2中Li与两个F相连成键,由于Li在与第一个F相连成键时它失去了电子,这个Li的电负性是提高了的,它再与第二个F相连成键时,Li总共减少的电子就远不像单键那么多了,而且还会影响已有的电子转移,平衡的结果是二F拉走的电子总量反而减少了。何况在(LiF)2中彼此是连接成环的,F连接的两Li是同时被另一个F拉走过电子电负性提高了的,拉过来的电子就少了,平衡结果就是实际的计算值。这里4个原子的单电子生成4个单电子键。
试想当一个F要从周围已经连有5个F的Li那里拉走电子会是多么不容易,在LiF晶体中,每个F只额外拉来0.2602,离子性只有26%,远远不能形成正负离子,何来离子键、离子晶体?
从F-1向Li+1配位的视角来看,F-1是用它的孤对电子去配位的,孤对电子受Li正离子吸引有部分进入到Li正离子的势场空间,双方达到电负性均衡。在(LiF)2中,第二个LiF的孤对电子来配位时,Li正离子已经接受了第一个LiF的部分配位电子,电负性已经有所下降,配位时转移电子的量就不会那么多了,并且第二个供电子的又会影响第一个的供电子,这样平衡下来,配位键总的转移的电子反而减少了。
特别是当Li正离子外面有6个LiF提供的配位电子时,Li正离子同时接受配位电子,这些电子又都在同一价壳层,各配位键相互排斥,所以配位键转移总的电子就反而大大减少了。
在LiF晶体中,由于一个Li外面有6个LiF配位,配位的LiF之间的键电子排斥是很大的,使得Li-F在晶体中拉开至2.01,而单个的Li-F优化键长为1.5955。相互之间键电子排斥使得电子不易流向Li。晶体中的这个键长,使得键中的Li与F的2 s不能参与成键,它在成键的MO系数中近乎为0,参加成键的只是向外延伸的2p,它在成键的MO系数中采用了高轨道p型基函数,大大延伸了。
图2(A)是Li(或F)周围有6个F(或Li)配位的微晶的一个Δρ的截面图。图中可以看到电子转移紧缩到F上的情况,还可以看到F与F之间是电子减少的深谷,Li-F键之间也是电子减少的深谷,它反映了LiF各键键电子之间是独立的、键电子之间是排斥的。也可以看到F向Li配位的形象和共享电子的成键区,以及晶体边缘的F合在一起反键区。
其实,原子分摊的参与成键的分子轨道系数,可以认为是广义的“杂化”,更加精确的杂化。
关于杂化,习惯上认为是原子的轨道预先主动杂化了去成键,其实应反过来想:电子在原子势场中成键时,因为键电子相互排斥,决定了方位、距离,才同时被动地决定了杂化,基函数线性组合系数就是来描述键电子在这种原子势场中各自分离的存在状态的。
在LiF晶体中,由于配位的键电子之间相互排斥,原子间距拉得很长,它们的延伸使得不够延展的2 s电子轨道都基本上退出了成键,使得2p的两瓣都可以分别去成键。如果像单键那样的键长成键,就是2sp杂化了,且用杂化后的较小的瓣单方向去成键,较大的瓣用来安排过多的转移电子。
对于被认为是典型的离子键LiF分子,虽然可以认为转移电荷达到了0.7002,离子性达到70%,但是电子多半还是落入反键区,不能认为成键是离子的正负电荷的静电吸引,成键还只是包含部分转移电子的整个成键区的共享电子。
对于LiF晶体,这里随着配位连接数的增多,逐步减少了像LiF分子那样的电子反键区,这反过来大大地抑制了电子转移量,当配位连接达到6时,全部反键区都失去了,只好把键大大抻长以便安排电子,转移电子只有0.2602,离子性只有26%。当然也可以把密集的配位键看成相互为反键区,反键区的功能转化为键电子之间的排斥,性质和作用是一样的。
键电子之间的排斥使得键上电荷向F转移量减少是LiF离子晶体的常态。
可见在LiF晶体中并没有形成正负离子,远远没有产生正负电荷的静电吸引而形成离子键,有的还只是极性共价键在成键区的电子共享。每个键上有一个分数电子,偏向F多了0.0433电子。
还可以算(NaCl)18的例子,同样求得它对各原子的电子密度差Δρ,图2(B)是它的中层截面的Δρ的等值线图,此层共有12个原子。
在(NaCl)18,从它的Δρ,可以找到与Na相连成键的各种Cl,用Multiwfn程序对这各种F在指定的空间进行盆积分,得到该原子上的电荷增加量如下(1、2是单独算出的):
与1个Na相连成键的Cl上的电荷转移量为0.6508。
与2个Na相连成键的Cl上的电荷转移量为0.6091。
与3个Na相连成键的Cl上的电荷转移量为0.5141。
与4个Na相连成键的Cl上的电荷转移量为0.4501。
与5个Na相连成键的Cl上的电荷转移量为0.4006。
与6个Na相连成键的Cl上的电荷转移量为0.3512。
6配位是该晶体内的实际情况,而且是6个键同时转移电子的总量,这是原子净电荷,单个键的转移量为0.0585。
还可以算(CaO)18的例子(也是NaCl型晶体),求得它对各原子的电子密度差Δρ,图2(C)是它的中层截面的Δρ的等值线图,此层共有12个原子。在(CaO)18,从Δρ可以找到与Ca相连成键的各种O,用Multiwfn程序对这各种O在指定的空间进行盆积分,得到该原子上的电荷增加量如下(2是单独算出的):
与2个Ca相连成键的O上的电荷转移量为0.9303。
与3个Ca相连成键的O上的电荷转移量为0.8132。
与4个Ca相连成键的O上的电荷转移量为0.6967。
与5个Ca相连成键的O上的电荷转移量为0.6049。
与6个Ca相连成键的O上的电荷转移量为0.5235。
6配位是该晶体内的实际情况,而且是6个键同时转移电子的总量,这是原子净电荷,单个键的转移量为0.0867。
对于上面电荷数据,不同的量子化学方法算的电荷数值是会有系统差别的,但是在同一种方法中所表现出的系列变化规律性和基本数量级还是符合实际可信可用的。
2.3. 电中性原理
上面数据表明,电负性大的F、Cl、O分别与电负性小的Li、Na、Ca配位成键生成离子晶体时,它们并不是电荷分离形成正负离子,带有或正或负的形式电荷,而是向F、Cl、O的电荷实际转移量出乎意料大大地减少了。
其实,Pauling早在1948年就写文章 [14] 论及此事,并提出了电中性原理(electroneutrality principle),后来又在再版的《化学键的本质》 [1] 中论述和应用了这个电中性原理。可见他早已从广泛的晶体实验中感悟到了这个客观存在的事实,并且把它归纳上升到原理的高度。
Pauling提出的电中性原理说:稳定的分子和晶体的电子结构,在于使每个原子上的净电荷接近于零(或介于±1单位电荷之间)。
在Pauling的化学键体系,一方面用形式电荷表达分子或者晶体的离子性,电荷可以多到几个正负电荷单位,这形式电荷有助于对离子晶体分门别类;另一方面又根据实际晶体实践经验感悟,提出了电中性原理,说分子和晶体每个原子上的净电荷很小、接近于零。上面实际计算的离子晶体中F、Cl、O的净电荷如此之小,证明电中性原理是符合客观实际的。
电中性原理和实际计算表明,分子和晶体的电子结构是每个原子上的净电荷很小、接近于零,由此派生了许多应用[1, 15]。
离子晶体常可以溶解于水生成水合离子,而又常常会标出这水合离子的形式电荷,于是好像印证了离子晶体中原子原本也具有同样高的离子电荷。
实际上,即使是水合离子,比如 [Fe(H2O)6]3+,它也不是Fe3+,而是正电荷分散在内层6个H2O的12个H上,以及外层更多水分子上 [15] ,它也符合电中性原理的概括,Fe的净电荷也会尽可能地小。
用考虑电子相关的post-HF方法MP2计算 [Fe(H2O)6]3+,体系电荷3+,5个单电子 [16] 。优化结构,水是用它的孤对电子与Fe3+配位的,见图2(D)。由于没有Fe3+的球对称化的原子波函数,不能作Δρ。净电荷取Mulliken atomic charges数据。此图6个水向Fe3+转移了大量的电子,转移量高达2.570,这使得原本3+的Fe的电荷只剩下+0.430,如果再加外层水分子,电荷还会更小。这充分体现了电中性原理。图2(D)中只标出了一个水分子的净电荷,所有水分子的净电荷数值是一样的。
还可以用DFT-D之B2PLYPD3 [17] 来计算一下,得到[Fe(H2O)6]3+中Fe的净电荷为+0.403。
本文虽然不认为有真正意义上的离子键、离子晶体,但还是不妨这么称呼,也是形式上的吧。只是不要仅停留在离子晶体或水合离子的形式电荷的层次上,以免受形式电荷的误导,而是要具体计算一下得到的实际的电荷量,来看待、分析离子晶体或水合离子,给电中性原理以具体的电荷数据支撑。
3. 结论
离子键、离子晶体的结合力,不是形成正、负离子引起的正负电荷的纯粹静电引力。离子键的转移电子多安排在反键区,离子晶体远不是真正形成正负离子,实际的转移电荷还很小,符合电中性原理。
离子键、离子晶体中的键,是极性共价键,这些键结合力的本质是原子对键上成键区的电子共享。
致谢
本文的计算由北京科音研究中心的卢天博士提供计算资源,并对此研究工作进行了讨论,特此致谢!