电网谐波电流小波变换实时检测研究

Real-Time Detection of Harmonic Current Wavelet Transform in Power Grid

摘要: 在对电网谐波治理和无功补偿时，需要实时检测分析电网中的谐波和无功电流，以便对电网中的谐波电流进行抑制和补偿无功功率。本文对小波变换算法在电网谐波电流检测中的应用做了研究，该算法利用mallat分解算法得到各频带的小波分解系数，然后将分解得到的小波系数进行单独重构，这样就可以分离出基波电流与各谐波分量。仿真与实验结果表明该方法可以很好的将基波电流与各谐波分离出来，能达到谐波电流实时检测的要求。

Abstract: In the harmonic control and reactive power compensation of the power grid, real-time detection and analysis of harmonics and reactive currents in the power grid are needed to suppress and compensate the reactive power in the harmonic current in the power grid. In this paper, the ap-plication of wavelet transform algorithm in power grid harmonic current detection is studied. The algorithm uses the mallat decomposition algorithm to obtain the wavelet decomposition coefficients of each frequency band, and then reconstructs the wavelet coefficients obtained by decomposition separately, so that the base can be separated. This allows the fundamental current and the harmonic components to be separated. The simulation and experimental results show that the proposed method can separate the fundamental current and each harmonic well, and can meet the requirements of real-time detection of harmonic current.

1. 引言

在电网供电系统中，电网电压是正弦交流电压，通常为50 Hz [1] 。当电网向电阻、电感、电容器等线性负载供电时，电流波形不变，仍为交流电。然而，当电网电压施加到非线性负载(如二极管整流器或交流电压调节器)时，电流波形失真，除了基本分量之外还包含谐波分量 [2] 。产生谐波的负载装置也是消耗基本无功功率的装置，它们在正常运行时给电力系统和电力用户带来危害。

综合国内外的研究现状，本文将现有谐波测量和分析的主要方法分四种：

• 基于傅立叶变换的谐波检测方法；

• 基于瞬时无功功率理论的谐波检测方法；

• 基于人工神经网络的谐波分析和检测方法；

• 基于小波变换的谐波分析与检测方法。

瞬时无功功率理论检测法、神经网络法是通过分析信号的时域信息，得出信号的基本参数。傅里叶变换及其改进算法是通过将时域变换为频域信息进行分析处理，降低了信号分析的难度 [3] 。很多情况下，要求不仅能够获取信号在时域和频域的全貌而且要得悉信号在某些时刻的局部特征，而单纯的时域或频域分析均无法满足此要求，有学者提出了小波变换。小波变换能够通过信号频率来调整时频窗口，能精确定位信号的时间和频率，从而能够更准确的检测电网谐波电流 [4] 。本文通过构建典型的电网谐波信号模型，利用mallat分析方法对谐波信号进行检测和分析，仿真结果表明此方法具有良好的时频局部化特性，适合于稳态谐波和时变谐波的检测分析。

2. Mallat算法

多分辨率分析，也称多尺度分析是建立在函数空间概念上的理论 [5] 。它主要是将 $L^2\left(R\right)$ 空间分解为一系列具有不同分辨率的子空间，然后将 $L^2\left(R\right)$ 中的函数 $x\left(t\right)$ 用各个子空间上的函数进行描述，即在各个子空间上进行投影，得到信号 $x\left(t\right)$ 在不同分辨率子空间上的特征，从而可以在不同的尺度上由粗及精地观察信号 [6] 。

在多分辨率分析中，尺度函数的双尺度方程和小波函数的双尺度方程可分别表示为

$\begin{array}{l}\varphi \left(t\right)=\sqrt{2}{\displaystyle \underset{n=-\infty }{\overset{+\infty }{\sum }}h\left(n\right)\varphi \left(2t-n\right)}\\ \phi \left(t\right)=\sqrt{2}{\displaystyle \underset{n=-\infty }{\overset{+\infty }{\sum }}g\left(n\right)\phi \left(2t-n\right)}\end{array}$ (1)

由此可以推出相邻尺度空间剩余系数和小波系数的关系为

$c_{j,k}={\displaystyle \underset{m=-\infty }{\overset{+\infty }{\sum }}h\left(m-2k\right)c_{j-1,m}}$ (2)

$d_{j,k}={\displaystyle \underset{m=-\infty }{\overset{+\infty }{\sum }}g\left(m-2k\right)c_{j-1,m}}$ (3)

Mallat算法是小波变换的快速算法，Mallat算法为小波变换在实际应用分析中奠定了基础，接下来我们对Mallat算法进行研究。

任意信号 $x\left(t\right)\in L^2\left(R\right)$ 在 $V_{j-1}$ 空间上展开为 [7]

$x\left(t\right)={\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{c}_{j-1,k}{2}^{\left(-j+1\right)/2}\varphi \left(2^{-j+1}t-k\right)}$ (4)

由式(4)有 $V_{j-1}=V_j\oplus W_j$ ，将 $x\left(t\right)$ 分解一次投影到 $V_j$ 和 $W_j$ 空间，得到信号 $x\left(t\right)$ 在 $V_j$ 下的粗像和在 $W_j$ 下的细节

$x\left(t\right)={\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{c}_{j,k}{2}^{-j/2}\varphi \left(2^{-j}t-k\right)}+{\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{d}_{j,k}{2}^{-j/2}\varphi \left(2^{-j}t-k\right)}$ (5)

其中 $c_{j,k}$ 为 $j$ 尺度上的剩余系数， $d_{j,k}$ 为 $j$ 尺度上的小波系数。式(5)中第一项为 $x\left(t\right)$ 在 $j$ 尺度空间的近似部分，第二项为 $x\left(t\right)$ 在 $j$ 尺度上的细节部分。由式(2)可知 $j$ 尺度空间的剩余系数 $c_{j,k}$ 和小波系数 $d_{j,k}$ 可以通过 $j-1$ 尺度空间的剩余系数 $c_{j-1,k}$ 经过滤波器系数组 $h\left(n\right)$ 和 $g\left(n\right)$ 后求得。那么，将 $V_j$ 空间的剩余系数 $c_{j,k}$ 进一步分解下去，可以得到 $V_{j+1}$ 和 $W_{j+1}$ 空间的剩余系数 $c_{j+1,k}$ 和小波系数 $d_{j+1}$ ，继续分解下去，可以得到任意尺度 $j$ 空间下的剩余系数和小波系数。

经过分解，可以得到信号 $x\left(t\right)$ 在各尺度空间的分解表达式

$x\left(t\right)={\displaystyle \underset{j=-\infty }{\overset{j}{\sum }}{\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{d}_{j,k}\left(t\right){\phi }_{j,k}\left(t\right)}}+{\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{c}_{j,k}\left(t\right){\varphi }_{j,k}\left(t\right)}$ (6)

与小波分解类似，可以由各尺度空间的剩余系数和小波系数对剩余系数进行重构，小波变化系数的重建公式为 [8]

$c_{j-1,m}={\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{c}_{j,k}\left(t\right)h\left(m-2k\right)+}{\displaystyle \underset{k=-\infty }{\overset{+\infty }{\sum }}{d}_{j,k}\left(t\right)g\left(m-2k\right)}$ (7)

3. 基于小波变换谐波电流检测

3.1. 电网电流的小波分解

本文采用多分辨率分析的Mallat算法对含谐波的电网信号进行分析，基于小波变换的多分辨率分析将含有谐波的电流信号分解成不同频率的块信号，将低频段上的结果看成基波分量，高频段为各次谐波分量，从而得到谐波信息 [9] 。

式(2)、式(3)描述的系数分解可以看作一个输入离散序列经过双通道滤波器的过程。最后由两个滤波器输出序列总的长度与输入长度保持一致 [10] 。

图1中，信号每次经过滤波器组 $\bar{h}$ 、 $\bar{g}$ 都进行2抽取，保证数据长度与输入长度保持一致。设电网电流信号 $x\left(t\right)$ 经过采样后得到的离散序列，它的最高频率为 $f$ ，序列长度为 $N$ 。将离散序列作为最高分辨率空间中的分量 $\overline{a_0}$ ，经过滤波器组 $\bar{h}$ 和 $\bar{g}$ 一次分解后得到频带为 $0~f/2$ 的细节分量 $d_1$ 和频带为 $f/2~f$ 的近似分量 $\overline{a_1}$ ， $d_1$ 和 $\overline{a_1}$ 的长度都为 $N/2$ 。将细节分量 $d_1$ 经过滤波器组 $\bar{h}$ 和 $\bar{g}$ 第二次分解，又可以得到频带为 $0~f/4$ 的细节分量 $d_{11}$ 和频带为 $f/4~f/2$ 的近似分量 $d_{10}$ ， $d_{11}$ 和 $d_{10}$ 的长度都为 $N/4$ ，这样经过n次分解可以得到频带为 $0~f/2^n$ 的细节分量和频带为 $f/2^n~f/2^{n-1}$ 的近似分量，它们的长度都为 $N/2^n$ ，直到的细节分量 $0~f/2^n$ 中只包含基波电流成分。

Figure 1. Schematic diagram of signal n-time decomposition

图1. 信号n次分解示意图

3.2. 基波电流的重构

电网电流信号 $x\left(t\right)$ 经过图1分解，得到了不同频带的小波系数，现在将基波分量单独重构，可以得到 $x\left(t\right)$ 中的基波电流成分。图2是由基波电流系数重建基波电流的示意图。

Figure 2. Schematic diagram of signal reconstruction

图2. 信号n次重构示意图

与图1相对应，在重构过程中为了保证恢复原信号的数据长度，将小波系数进行插2处理。

3.3. 仿真分析

采用小波变换原理对三相整流器带阻感负载时的电流进行谐波电流检测仿真实验，在saber仿真软件中建立图3所示的电路模型，其中，负载电阻 $R=10\Omega$ ，负载电感 $L=1\text{mh}$ ，采用小波分析进行谐波检测，在实验中，采样频率9.6 KHz，分解层数是5层，采用db 8小波，采用周期扩展来扩展边界。根据Nyquist采样定理，原始信号包含的频带0~4.8 KHz，最高谐波为96次谐波。

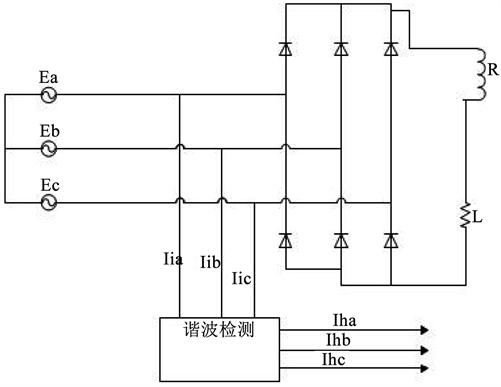
Figure 3. Harmonic detection circuit structure

图3. 谐波检测电路结构图

根据小波变换理论，小波变换谐波检测算法分为以下几步：

l 确定小波空间。将采样信号谐波电流 ${\text{i}}_{\text{la}}$ 根据谐波成分进行小波分解。基波电流系数位于第5层低频概貌中。

l 进行5层小波分解，将 ${\text{i}}_{\text{la}}$ 作为 $V_0$ 空间的低频 $C_{0,k}$ ，对信号进行5次2抽取，保证数据总长度与输入信号长度相等。得到不同频率段的小波变换系数。

l 将基波电流小波系数 $C_{5,k}$ 单独重构，得到基波电流 $C_5$ 。

l 在电网电流中减去得到的基波电流就可以得到谐波电流。

在利用小波变换对电网电流进行实时分解与重构时，需要将当前的信号进行扩展。由于电网电流的周期性，本文采用周期扩展的方法，采用上一个周期的信号数据对当前数据进行扩展。那么电网电流的稳定性也就决定了该算法的检测精度 [11] 。

对于负载恒定时电网电流检测进行小波变换谐波电流分析。保持图3中负载恒定，采用小波分析对电网电流进行谐波实时检测。图4是检测出的基波、分离出的各次谐波电流和谐波电流波形。

图4电网电流波形幅值为53.46 A，基波电流为53.41 A。从图5中可以看出检测出来的基波电流基本不包含谐波电流，也体现出基波电流已经从电网电流中完全分离出来了，从图5中也体现出能将各次谐波从电网电流中分离出来。仿真结果表明了基于小波分析的谐波实时检测具有较高的检测精度。

Figure 4. Detected fundamental current, separated harmonic currents and harmonic current waveforms

图4. 检测出的基波电流、分离出的各次谐波电流与谐波电流波形

Figure 5. Grid current, fundamental current and separated harmonic current spectrum

图5. 电网电流、基波电流与分离后的谐波电流频谱图

4. 全文总结

本文主要研究了小波分析在电网谐波电流实时检测中的应用。分析了基于小波变换谐波电流检测的原理，对恒定负载下的检测过程进行分析，仿真结果表明了小波变换具有时频局部化检测信号的能力，可以对谐波信号进行频带划分，提取各次谐波信息，基于小波分析的谐波实时检测具有较高的检测精度。