1. 引言
服装结构设计涉及大量几何计算和作图,传统的方法利用经验公式和参数简化计算,曲线的生成主要凭制版师的经验和感觉,图形的绘制也完全依赖于制版师的手工操作 [1] 。因此其整个服装结构设计过程既重复、繁琐,又极不精确,且容易出错。由于服装生产具有多品种、小批量、短周期的特点,传统的手工制图已无法满足这种需求。
服装CAD制版系统利用计算机强有力的计算功能和高效率的图形处理能力,辅助完成设计中的计算、分析、模拟、制图、编制等工作 [2] ,减少手工计算环节,提高设计质量、加快服装产品的研发,提高服装工业的生产效率。但是在服装CAD制版系统中,服装结构曲线仍是由制版师手动绘制或者拖拽生成,制版师依旧重复大量且琐碎的绘图工作 [3] ,致使整个服装制版效率不高。
服装结构曲线自动生成是智能化服装CAD制版系统主要功能之一 [4] 。不同种类服装结构曲线需要大量不同的公式推导,计算机在计算曲线参数时,就会遇到计算复杂度高和计算量大等问题。服装曲线数字化模型的选择和参数的简便计算成为了服装结构曲线自动生成的难点。
为了使服装结构曲线不再依赖于制版师的手工操作,通过研究服装结构曲线的绘制过程,以衬衣后片版型为例,提出一种基于贝塞尔曲线控制点的曲线自动绘制方法,实现了服装结构曲线绘制自动化,可用于基于参数设计的服装CAD制版系统,加快了服装制版速度,提高服装制版效率。
2. 相关工作
在计算机辅助设计中,常用到多项式插值曲线、参数样条曲线、贝塞尔曲线或者B样条曲线来拟合工业制造中的各种曲线 [5] 。文献 [6] 总结了多种服装CAD中常用的曲线和其应用特性,为服装CAD开发技术人员提供理论依据和准确的数学模型。这些曲线分别是参数样条曲线、贝塞尔曲线、3次Hermite样条曲线和B样条曲线。同参数样条曲线和B样条曲线相比,贝塞尔曲线的特点是能够非常方便的构造并且得到的曲线其内部拼接点处具有很好的光滑性, 整体线条优美 [7] 。
王姝 [8] 通过比较常用服装设计中曲线的优劣及适用场合,发现了贝塞尔曲线能够比较准确的通过控制多边形来确定服装结构图形的曲线;张建桥 [9] 使用了二阶贝塞尔曲线来表示服装结构曲线,同时利用贝塞尔曲线的端点性质实现了相邻曲线的“光顺”连接;宋琨和张渭源 [10] 等通过分析服装结构曲线的一些共同点,提出使用三次贝塞尔曲线拟合,可以满足服装结构中可能遇到的各种类型的曲线。
在现有的贝塞尔曲线计算机算法常使用:Bezier定义作图法 [11] 、依曲率变化的非均匀取点逼近法 [12] 、圆弧样条逼近法 [13] 和定比分割判别计算法 [1] 。
定义作图法是利用参数方程计算出密集点连接而成,因其计算量过大只适合计算机辅助人工绘图。
依曲率变化的非均匀取点逼近法仅使用整型数运算并无需乘除法运算,与传统方法相比有较快的运算速度但其计算量相近。
圆弧样条逼近法采用单、双圆弧样条结合的方法来拟合三次贝塞尔曲线。先把曲线分成N段,其中前N – 1段用单圆弧样条逼近,最后一段用双圆弧样条来逼近并且保证了一阶几何连续。虽然其计算量相比传统方法较少,但是存在一定的误差,精准度不高。
定比分割判别计算法与本文类似,其利用参数方程中的参数离散程度(定比分割性质)来控制迭代计算以及绘图精度,还介绍了如何通过已知条件求解出贝塞尔曲线的控制点,再用上面提到的算法绘制出所要求的贝塞尔曲线。作者所讨论的已知条件只包括已知曲线的端点和端点处的切方向,或者已知曲线的端点以及端点联线中点处的凹势。
本文所提出的方法与定比分割判别计算法不同之处在于本方法可以根据已知曲线上点的坐标计算贝塞尔曲线的控制点及绘制。同时定比分割判别计算法不具有一般性,对于服装结构设计的不同结构不同曲线,都需要大量的公式推导和繁琐计算,才能得出较为精确的服装结构曲线,大大增加了编程难度和服装结构数字化的工作量,而本文所提出的方法只需已知服装结构某一曲线上4个点,并不考虑不同服装结构的曲线类型,更具有普遍性。实验证明算法耗时少且误差小,算法整体复杂度低。
3. 服装结构曲线拟合
3.1. 服装结构曲线特征
在服装CAD中,需要将服装设计师绘制的设计图转变成1:1的版型图。版型图是由直线和各种曲线组合成的几何图形,其中曲线种类繁多,不同种类的曲线形态差别很大,如袖笼线、衣领弧线等。
以衬衫后衣片为例,其版型图由8条直线和5条曲线拼接构成,如图1所示。这些曲线分别是① 衣领弧线、② 袖笼线、③ 腰围弧线、④ 臀围弧线以及⑤ 下摆线。
各类曲线在手工制版中是按照一定设计原则和经验公式,依次连接若干设定的点再光顺连接。即服装结构曲线是由依次连接n (n ≥ 1)个点形成的光滑曲线 [10] 。图2是一名资深制版师的衬衣后片版型图,保留了制版过程。
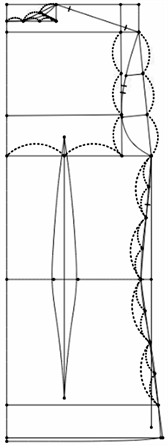
Figure 2. Back plate of the shirt layout with pattern process
图2. 含制版过程的衬衫后衣片版型图
图2中衣领弧线放大后为图3。其中P0,P1,P2,P3是曲线上的4点;图中的虚线代表了服装制版师绘制该曲线时的公式或者该曲线的设计原则,即P5是基础线段P0P4的1/3点,P1在P5上0.1 cm,P6是辅助线段P5P3的中点,P2是辅助线段P6P4的1/4点。由此确定了P0,P1,P2,P3的位置,然后在依次光顺连接,得到了衣领弧线。
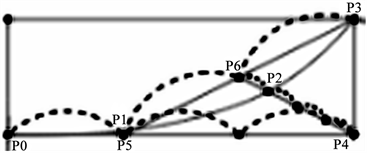
Figure 3. Collar arc layout with pattern process
图3. 含制版过程的衬衫后衣片衣领版型图
结合图2所示,由服装结构设计原则和制版经验公式可知,每种曲线都可以找到经过曲线上的4个固定点。但在服装CAD制版系统中,每条曲线经由制版师手动拖拽生成,不断调整控制点进行绘制。为了使服装结构曲线绘制不在依赖于制版师的手动操作,计算机必须通过计算得到控制点才能实现自动绘制各种曲线的功能。
3.2. 服装版型结构常用曲线
3.2.1. 贝塞尔曲线 [5]
贝塞尔曲线广泛应用于许多图形系统和CAD系统。由于其具有许多较好的性质,在曲线和曲面设计中,贝塞尔曲线更实用且更容易实现。
根据2.1节中服装结构曲线的特征,本文选取三次贝塞尔曲线作为服装结构曲线的数字化模型,其造型有C型曲线和S型曲线,如图4(a),(b)所示。
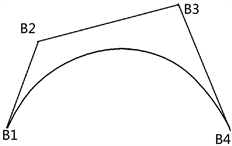 (a) C型曲线
(a) C型曲线 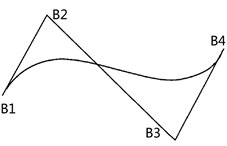 (b) S型曲线
(b) S型曲线
Figure 4. Shape of Bézier curve
图4. 贝塞尔曲线造型
三次贝塞尔曲线适用于服装结构各种曲线。常用C型曲线绘制袖笼线、领子弧线和下摆线;S型曲线绘制腰围弧线和臀围弧线等,如张建桥 [9] 在其设计的服装CAD原型设计系统中,以袖笼线为例,根据服装制版公式,计算相应位置点,使用贝塞尔曲线进行绘制。但其需要事先对不同种类的曲线进行相应公式计算和推导,因此不具有普遍性。
3.2.2. NURBS曲线 [5]
NURBS曲线在CAD与计算机图形学领域也具有广泛的应用,比贝塞尔曲线更能精确地表示自由型曲线;但由其数学表达式可知,除了需要计算控制点之外,还需要设置权因子和分析节点矢量。如刘庚鑫使用NURBS曲线绘制袖笼线时,选取了曲线上3个切向量作为节点矢量 [14] 。虽然其绘制袖笼线精度较高,但每种曲线都需要去额外分析其特征来获得节点矢量,导致计算工作量增加和复杂度提高。相比较而言,贝塞尔曲线则不需要这些工作,其精确度也能符合服装结构曲线的要求。
4. 贝塞尔曲线的控制点计算方法
三次贝塞尔曲线均由两个端点和两个柄点,一共四个控制点进行控制,其具体参数形式如式(1)所示:
(1)
式中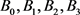 为相应的控制点;
分别为曲线的起点和终点。
为相应的控制点;
分别为曲线的起点和终点。
改变一个控制点的坐标,曲线的形状将随之改变。如图4中,控制点
的改变使得贝塞尔曲线从C型变化为S型。对于每个控制点的改变,均会影响这段曲线所有部分,控制点对曲线具有整体控制性 [15] 。
贝塞尔曲线在计算机绘制中通常都会使用相应的数学库函数,如JS的bezier Curve To,C++的Poly Bezier,Android的cubic To等。这些函数都需要贝塞尔曲线的控制点作为参数输入,如bezier Curve To (cp1x, cp1y, cp2x, cp2y),其中cp1x表示第一个贝塞尔控制点的x坐标,以此类推。在本文中,已知条件是曲线上的4个点,如何利用这4个点计算出曲线的控制点成为本文的重点。
4.1. 基于梯度下降法的控制点计算方法
梯度下降法是沿梯度下降的方向求解表达式
的极小值。选取定义域内任意初始点
,从
出发沿着负梯度方向走,可使得 下降最快,迭代公式如式(2)所示:
下降最快,迭代公式如式(2)所示:
(2)
式中: 表示在
处的梯度,负号表示沿梯度的负方向;
表示在
处的梯度,负号表示沿梯度的负方向;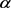 是梯度方向上的步长即学习效率。
是梯度方向上的步长即学习效率。
在本文中,设已知点
,假设4个控制点
,其中
。以
的
为例,初始控制点选择曲线上4个点A,B,C,D,此时的贝塞尔方程如式(3)所示:
(3)
取101个点即作为样本点,代入贝塞尔方程可得坐标,表示为
;同时也可以由三次多项式方程计算出101个点的曲线上实际坐标,表示为
。
梯度公式变换为式(4):
(4)
式中:
迭代公式如式(5)所示:
(5)
式中:n表示迭代次数。
同理可以算出
;整个算法的终止条件为
4.2. 基于解方程组法的控制点计算方法
若给定(n + 1)个固定点
,为了构造一条通过这些固定点的n次贝塞尔曲线,需要反求出通过
的贝塞尔曲线的(n + 1)个控制点
。
1) 传统方法
通常可根据固定点
的参数t用于反求
,由贝塞尔曲线定义可得到关于
的(n + 1)个方程构成的线性方程组如式(6)所示:
(6)
式中:
;
为
在贝塞尔曲线上的参数。
由上述方程组可解过
的贝塞尔曲线的(n + 1)个控制点
。分别代入
的坐标即方程组关于
的(n + 1)个方程式,可解出(n + 1)个控制点
的坐标值
。
2) 改进的解方程组法
由于本文中的固定点
的参数
未知,难以求解传统方法中的方程组。做出如下的改进,取参数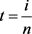 与之对应的新固定点
。令
与之对应的新固定点
。令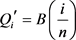 ,由此可得到新的关于
的(n + 1)个方程构成的线性方程组如式(7)所示:
,由此可得到新的关于
的(n + 1)个方程构成的线性方程组如式(7)所示:
(7)
在本文中,n取4,则三次贝塞尔曲线对应的4个控制点的线性方程组如式(8)所示:
(8)
分别代入对应固定点的坐标值即可求解对应的控制点坐标。
5. 曲线绘制实验
以图3的领子弧线为例,在服装设计中,该曲线的详细数据如下:线段P0P4 = 7.1 cm,线段P3P4 = 2.4 cm。按照所述的该曲线的绘制方法,以P3为x轴,以P0为y轴,通过计算得到4个点的坐标分别P0 (0, 2.4),P1 (2.3667, 2.30),P2 (5.3249, 1.5),P3 (7.1, 0),进而使用最小二乘法进行线性拟合曲线,得到的多项式方程式的各个系数为A = −0.00955545,B = 0.02350724,C = −0.02323944,D = 2.4。
在html5.0的canvas画布中,绘制了该曲线。为了更清晰的看清曲线,把坐标系放大了100倍,如图5所示。
由图5可知,使用最小二乘法线性拟合的曲线局部有可能会出现不连续的情况,如图中圈滑部分。整体曲线不够光滑,不符合服装结构曲线“光顺”的要求。
5.1. 贝塞尔曲线的控制点计算和绘制
梯度下降法除了4.1所提到的初始条件外,还需要根据实际情况初始化步长
和
。本文选取3个不同步长进行测试;同时
选取了0.01,结果如表1所示:
在html5.0的canvas画布中,使用js的bezierCurveTo函数绘制了表中的贝塞尔曲线。使用图5中的坐标系,绘制结果如图6(a),(b),(c),(d)所示,图中4个黑点表示曲线上已知的4个点。

Table 1. Calculation results of Bézier curve control point
表1. 贝塞尔控制点的计算结果
注:1,2,3号曲线控制点的计算方法为梯度下降法;4号曲线控制点的计算方法为解方程组法。
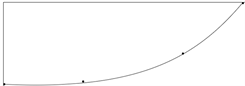 (a) 曲线编号1
(a) 曲线编号1 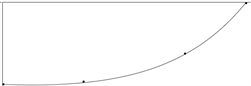 (b) 曲线编号2
(b) 曲线编号2  (c) 曲线编号3
(c) 曲线编号3  (d) 曲线编号4
(d) 曲线编号4
Figure 6. Linear fitted curves
图6. 贝塞尔曲线绘制结果
由图7可知:由2种方法计算得出的控制点进行绘制的贝塞尔曲线仍有小部分的偏差。可能的原因是:梯度下降法是在终止条件下得出最优的极值。
越小,理论上所绘制的曲线越准确的,但其带来的计算时间成本是非常庞大。解方程组法所采用的初始点并不是原来曲线上4个点,事先很难清晰地知道曲线上4个点在曲线的位置(即参数t);但可以通过多项式方程轻松地计算得到三等分点,这样就不能保证该方法生成的曲线一定经过原始的4个点。以上就是误差可能产生的原因。
5.2. 曲线的误差分析
为了更具体地比较2种方法,通过计算贝塞尔曲线上的均匀100个点与原曲线上的100点的距离和进行误差分析,误差函数为
。如果曲线上的比较点数量较少,误差和就可忽略不计,故适取100个点。具体数值如表2所示。
实验结果:在服装结构设计中,是允许有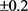 的误差;2种方法计算得到的曲线都是满足要求的;但梯度下降法耗时普遍过长,且精确度越高,需要时间则更多。解方程组法的误差较小且时间成本可以忽略不计。在计算贝塞尔曲线的控制点时,可以优先选用解方程组法进行求解。如果解方程组法得到的控制点有较大偏差或者不符合该曲线的设计准则,可以使用梯度下降法进行优化和调整。综合时间成本和精确度,梯度下降法的参数
和
默认都取0.01。
的误差;2种方法计算得到的曲线都是满足要求的;但梯度下降法耗时普遍过长,且精确度越高,需要时间则更多。解方程组法的误差较小且时间成本可以忽略不计。在计算贝塞尔曲线的控制点时,可以优先选用解方程组法进行求解。如果解方程组法得到的控制点有较大偏差或者不符合该曲线的设计准则,可以使用梯度下降法进行优化和调整。综合时间成本和精确度,梯度下降法的参数
和
默认都取0.01。
5.3. 曲线绘制自动化的应用
在基于参数的服装CAD制版系统中,可直接使用本文中的曲线控制点计算方法。按照例如表3中的服装版型参数和预先存储好的服装结构曲线设计公式,系统将自动生成服装版型原型图,如图8所示。

Table 3. Parameters of shirt back plate
表3. 衬衫后衣片版型参数
制版师将不在用手动拖拽控制点方式进行绘制及调整曲线;只需通过修改服装版型参数,系统将自动绘制及调整服装结构曲线,快速生成服装版型图。系统开始会使用基于解方程组法的控制点计算方法绘制曲线。如果自动绘制曲线的效果或者精确度令制版师不满意,制版师可向系统发送重新绘制请求。系统后台将采用基于梯度下降法的控制点计算方法重新自动绘制曲线,但由于其计算时间较长,不能马上出结果,需要制版师等待一段时间。
综上所述,本文实验将基于解方程组法的控制点计算方法作为曲线绘制的首选方法,基于梯度下降法的控制点计算方法作为曲线绘制的备用方法。结合3.1节中提到的服装结构曲线的设计原则和公式,自动绘制服装版型图,实现了服装CAD制版系统中曲线绘制自动化功能。
6. 结论
本文提出一种基于贝塞尔曲线控制点的服装结构曲线绘制自动化的方法。该方法仅依赖于经过曲线的几个固定点并且能够自动计算其曲线控制点。这些固定点是通过服装结构曲线的设计原则得到的,不再由制版师人工拖拽获得。实验证明其精确度符合服装结构设计的要求。相较于传统服装CAD制版系统中的曲线绘制,服装结构曲线生成将不再过多依赖于制版师的手工操作,而是结合具体服装结构设计中的数据标准和经验公式,运用本文的方法自动计算控制点,自动生成服装结构曲线,实现了服装CAD制版系统中曲线绘制自动化的功能,减少制版师不必要的重复工作,使得服装结构设计更加高效和便捷。
基金项目
东莞市专业镇创新服务平台建设项目“东莞市虎门服装协同创新中心”;广东省协同创新与平台环境建设专项资金。
参考文献