基于从头计算势能面的H + HS反应的理论研究

Theoretical Study of the Reaction H + HS Based on the Ab initio Potential Energy Surface

摘要: 利用准经典轨线方法计算了基于最新三重态势能面H + HS→S + H2反应的动力学性质。反应几率和反应截面与含时波包方法计算的结果吻合的非常好。计算结果表明在低能区碰撞能效的提高了反应的活性，而在高能区碰撞能则抑制了该反应的进行。另外，反应产物H2分子主要向前和向侧边散射，碰撞能对散射强度和方向影响较大。

Abstract: Quasi-classical trajectory (QCT) method has been used to calculate the dynamics of the reaction H + HS→S + H2 on the newly developed potential energy surface of lowest triplet state. The agreement of reaction probability and integral cross section between QCT and time-dependent wave packet (TDWP) calculations are fairly good. The results suggested that the collision energy enhances the reactivity in the low collision energy range, whereas inhibits the reaction at relatively high energies. In addition, the product molecules H2 are mainly scattered forwards and sideways, and the scattering intensity and direction are sensitive to the collision energy.

1. 引言

近年来，人们发现包含S-H键的最简单分子HS和H₂S在燃烧和大气化学中扮演重要角色。因此无论在实验上还是在理论计算上，H + HS反应都受到了广泛的关注。众所周知，反应体系的势能面决定了反应过程的动力学性质。早在1983年Martin等人利用完全活性空间自洽场(CASSCF)计算了 $\text{H}+\text{HS}\to \text{S}+{\text{H}}_{\text{2}}$ 的第一个势能面 [1] ，随后Maiti等人在两个最低三重态势能面( $1{}^3{A}^{\prime }$ 和 $1{}^3{A}^{″}$ )上研究了系间窜跃效应 [2] ，准经典轨线TSH (Trajectory Surface Hopping)计算结果表明系间窜跃造成的强电子淬灭在反应中起着很重要的作用。然而在2010年Lara等人提出碰撞过程中产生的中间产物最终通过反应分解为产物或者通过电子淬灭分解为基态反应物 [3] 。这一结论与文献 [2] 得到的结果恰好相反。运用多参考组态相互作用方法(MRCI) Zyubin构建了H₂S体系的从头算势能面 [4] ，并利用该势能面研究了S(¹D) + H₂/D₂反应的动力学性质。利用相同的从头算数据，Ho等人为H₂S体系构建了一个改善的基态势能面 [5] ，然而基于改善后势能面的准经典轨线计算结果与文献 [4] 十分接近。最近，吕双江利用多参考组态相互作用以及完全活性空间自洽场方法构建了一个高精度的最低三重态势能面 ${}^3{A}^{″}$ [6] ，研究显示H + HS反应的提取通道和交换通道的过渡态均为直线型构型，分别位于 $R_{\text{HH}}=\text{2}.\text{54}{a}_0$ 和 $R_{\text{HS}}=\text{2}.\text{62}{a}_0$ 处，以及 $R_{\text{HH}}=R_{\text{HS}}=2.87a_0$ 处，其中提取通道势垒高为0.091 eV。文章作者利用准经典轨线方法(QCT)和量子含时波包方法(TDWP)在0~2.0 eV能量范围内计算了H + HS反应的反应几率和积分反应截面。计算结果表明，由于提取反应能垒较低，在低碰撞能区反应就比较容易进行，而一旦碰撞能超过交换反应势垒，交换反应很快占据优势地位。从目前已有的文献来看，实验方面对H + HS反应的测量主要集中在对热速率常数的测定上面，而且绝大多数的都是在室温下执行。理论方面则主要集中在对碰撞反应过程标量性质的研究，而反应过程的矢量性质即立体动力学性质对于全面理解H + HS反应的微观机制具有重要意义。本文利用准经典轨线方法在文献 [6] 新构建的势能面上，详细地研究了 $\text{H}+\text{HS}\to \text{S}+{\text{H}}_{\text{2}}$ 反应的立体动力学性质，期待计算结果能对该反应的物理图像进行补充完善。本文的结果将对该势能面的准确性进行验证，并对实验上利用交叉分子束技术研究该反应以及类似的氢原子提取反应的空间动力学提供一定的参考意义。

2. 理论

运动及碰撞过程矢量在空间的分布需要在选定的质心坐标系中进行描述。图1为质心坐标系及其与矢量方向间的关系图。其中z轴平行于反应物相对速度矢量k，y轴垂直于k、 $k^{\prime }$ 组成的散射平面(xy面)， $j^{\prime }$ 表示产物的转动角动量。两矢量k、 $k^{\prime }$ 与坐标轴的夹角用 $\left(\theta ,{\theta }_r,{\varphi }_r\right)$ 来表示。散射角 $\theta$ 为反应物相对速度与产物相对速度方向的夹角，而 ${\theta }_r$ 和 ${\varphi }_r$ 则分别代表产物的角动量在质心坐标系下的二面角和方位角。

Figure 1. The xyz center-of-mass (CM) reference frame describing the vector correlations

图1. 描述矢量相关的xyz质心坐标系

在质心系中研究反应碰撞过程中的三个矢量k和 $k^{\prime }$ 以及 $j^{\prime }$ 的空间相关可以用以 $\left(\theta ,{\theta }_r,{\varphi }_r\right)$ 为变量的几率密度函数 $P\left(\cos \theta ,\text{cos}{\theta }_r,{\varphi }_r\right)$ 来描述，以修正的球谐函数 $C_{kq}^{*}\left({\theta }_r,{\varphi }_r\right)$ 为基函数将几率密度展开：

$P\left(\cos \theta ,\text{cos}{\theta }_r,{\varphi }_r\right)={\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{\displaystyle \underset{q=-k}{\overset{k}{\sum }}\frac{2k+1}{4\text{π}}}}\times \left(\frac{2\text{π}}{\sigma }\frac{\text{d}{\sigma }_{kq}}{\text{d}\omega }\right)C_{kq}^{*}\left({\theta }_r,{\varphi }_r\right)$

其中 $\sigma$ 是积分反应截面，散射角依赖的展开系数 $\frac{2\text{π}}{\sigma }\frac{\text{d}{\sigma }_{kq}}{\text{d}\omega }$ 称为极化依赖微分反应截面(PDDCS)。

在质心坐标系中，全相关的角分布 $k-k^{\prime }-j^{\prime }$ 可以用二面角分布函数 $P\left({\varphi }_r\right)$ 来描述，可以展开为傅里叶级数的形式：

$P\left({\varphi }_r\right)=\frac{1}{\text{2π}}\left(1+{\displaystyle \underset{even,n\ge 2}{\sum }{a}_n\cos n{\varphi }_r}+{\displaystyle \underset{even,n\ge 1}{\sum }{b}_n\sin n{\varphi }_r}\right)$

这里 $a_n=2\langle \cos n{\varphi }_r\rangle$ ， $b_n=2\langle \sin n{\varphi }_r\rangle$ 。在本计算中， $P\left({\varphi }_r\right)$ 展开到n = 24，分布函数结果就收敛了。

描述 $k-j^{\prime }$ 关联的 $P\left({\theta }_r\right)$ 分布可以展开为一系列的Legendre多项式：

$P\left({\theta }_r\right)=\frac{1}{2}{\displaystyle \underset{k}{\sum }\left(2k+1\right)a_0^{\left(k\right)}{P}_k\left(\cos {\theta }_r\right)}$

这里的展开系数 $a_0^{\left(k\right)}$ 称为定向系数(奇数)或取向系数(偶数)，可以用下式表示：

$a_0^{\left(k\right)}={\displaystyle \underset{0}{\overset{\text{π}}{\int }}P\left({\theta }_r\right)P_k\left(\cos {\theta }_r\right)\sin {\theta }_r\text{d}{\theta }_r}=\langle P_k\left(\cos {\theta }_r\right)\rangle$

本文利用标准的准经典轨线理论研究了碰撞能对反应的立体动力学性质的影响。根据已有大量研究表明准经典轨线方法在处理大部分三原子体系反应是非常有效的 [7] [8] 。在计算过程中利用数值积分的方法求解哈密顿运动方程，积分采用四阶Runge-Kutta-Gill法和Hamming修正的四阶Adams-Moulton预测校正法。反应物分子轴的初始取向和振动初相位利用Monte Carlo理论随机取样。计算条件如下：反应物分子HS处于基态(v = 0, j = 0)，碰撞能范围为0~2 eV，能量格点为0.1 eV，每个能量点计算2万条轨线。初始入射原子与靶分子之间的距离设置为30 Å，积分步长为0.1 fs，该时间数值足够小赖保证能量和角动量的收敛。在角动量J = 0和碰撞参数b = 0时，反应几率由P = N_R/N_T来确定，其中N_R为反应的轨线数目，N_T为计算的总轨线条数即2万。每条轨线的碰撞参数b通过b²在0到 $b_{\max }^2$ 范围内随机选取得到。一旦计算得到反应几率，反应的积分反应截面就可以由下式给出 ${\sigma }_R=\text{π}{b}_{\max }^2\lim N_R/N_T$ 。H原子与HS分子的碰撞可以通过三个通道来进行，分别是H原子交换通道 $\text{H}+{\text{H}}^{*}\text{S}\to \text{HS}+{\text{H}}^{*}$ ，H原子提取通道 $\text{H}+\text{HS}\to \text{S}+{\text{H}}_{\text{2}}$ 以及弹性碰撞不反应通道 $\text{H}+{\text{H}}^{*}\text{S}\to {\text{H}}^{*}\text{S}+\text{H}$ 。本工作主要研究提取通道反应，即反应产物为H₂分子。

3. 结果和讨论

为了验证准经典轨线方法处理该反应的可靠性，我们首先计算了反应的反应几率并与已有的精确的量子方法结果进行比较。图2给出了碰撞能在0~2 eV范围内角动量为零的条件下 $\text{H}+\text{HS}\left(v=j=0\right)\to \text{S}+{\text{H}}_{\text{2}}$ 的反应几率。本文计算的结果用圆点和正方形表示，文献 [6] 利用含时波包方法计算的结果用虚线表示。从图中可以看出准经典轨线计算的结果与含时波包方法计算的结果吻合的非常好，这说明量子效应例如零点能和隧穿效应在该反应中并不明显，对反应的动力学性质影响不大。由于该反应路径不存在势阱，只有一个能量为2.07 kcal/mol的小垒，因此反应的阈值较小。计算结果也同样显示只要能量超过0.05 eV，反应就会进行。随着碰撞能的增加，反应几率越来越大。当碰撞能处于0.4到1.2 eV之间时，反应几率几乎不会发生变化，而一旦超过1.2 eV，反应几率将会逐渐减小。这是因为此时增加的碰撞能大部分转化为促进交换反应的有效能。这说明在低能区，反应产物H₂占据比重较大，随着碰撞能量的增加，促进反应进行的有效能并没有增加，而在高能区，交换得到的产物HS占据优势地位。这一点可以从反应的总几率即交换反应和提取反应几率之和看出。图中的正方形表示总反应几率，其随着碰撞能的增加一直在增大，这间接说明碰撞能对交换反应一直起促进作用。更重要的是，交换反应在整个碰撞能区间都占据主导地位。从趋势图上可以看出，在大于1.8 eV的更高能量区，提取反应几率几乎为零。

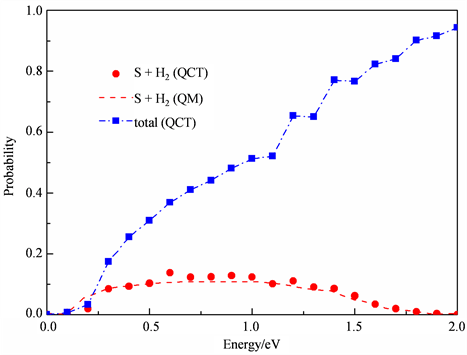
Figure 2. Comparison of the reaction probabilities between the QCT and TDWP calculations over the collision energy range of 0 to 2.0 eV

图2. 在0到2.0 eV碰撞能间利用准经典和量子含时波包计算得到的反应几率的对比

图3计算了 $\text{H}+\text{HS}\left(v=j=0\right)\to \text{S}+{\text{H}}_{\text{2}}$ 反应的积分反应截面，并与文献 [6] 利用耦合通道(CC)方法的结果进行了比较。很明显，两种方法计算的结果符合的很好。结果表明碰撞能在反应过程中扮演了重要的角色。积分反应截面并没有显示阈值，在低能区迅速的达到1.61 Ų，然后随碰撞能的增加较柔和的降低，这种行为符合势能面无垒或者小垒的动力学情形。由于积分反应截面取决于反应轨线百分比和碰撞参数b，从图2可以看出，在0.4到1.2 eV区间内的反应几率几乎保持不变，而在观察计算过程中随机取得的碰撞参数在此碰撞能区间变化也不大，这导致了积分截面的变化也很小。总之碰撞能在低能区提高反应的活性，但是在高能区则抑制了反应的进行。另外，在高能区1.3~2.0 eV间，准经典计算的结果略高于量子计算的结果。这是由于准经典轨线理论在处理反应过程中无法处理量子效应，例如零点能和隧道贯穿效应。尽管该反应在低能情况下的量子效应不明显，但在能量较大的情况下，很明显隧道贯穿效应对反应的影响逐渐体现，这导致量子结果比准经典结果要稍微大一些，而且随着能量的不断增大，这种差异也越来越大。

Figure 3. Comparison of the integral cross sections between the QCT and CC calculations over the collision energy range of 0 to 2.0 eV

图3. 在0到2.0 eV碰撞能间利用准经典和耦合通道计算得到的积分截面的对比

立体动力学的研究能帮助更好的理解碰撞能对反应的影响。图4描述了5个典型碰撞能下 $k-k^{\prime }-j^{\prime }$ 相关以及产物散射角分布的极化依赖的微分反应截面(PDDCSs)。图示的纵坐标P₀₀即 $\left(2\text{π}/\sigma \right)\left(\text{d}{\sigma }_{00}/\text{d}{\omega }_t\right)$ 表示简单的微分散射截面(DCS)，只表示产物分子的散射方向，与产物角动量的取向和定向并不相关。从图上可以看出H₂产物分子在0.4 eV的低能量下主要是向侧边和略微的向后散射，在 $\theta ={100}^{\circ }$ 处产生一个峰值，表明大量产物分子在该角度处散射强度最大。随着碰撞能的增加，产物分子H₂逐渐变得向前散射，并且散射强度对应的峰值角度也逐渐减小。这归因于该反应的机制属于直接反应，在碰撞能的增加下，产物的向前散射更加明显，这主要是由于冲击效应造成的。另外一般而言，对于三原子反应体系例如 $A+BC\to AB+C$ ，如果势能面是排斥型的，则产物分子倾向于向后半球散射。而对于吸引型势能面，则产物分子优先向前半球散射。此体系所采取的势能面特征是吸引的，导致理论上产物分子H₂应大部分向前散射。我们可以利用韩克利等人提出的质量组合模型合理的解释这种异常现象。他们经过研究发现质量组合对产物空间分布的影响要大于势能面对其分布的影响。H + HS反应体系属于典型的轻–重–轻模型，在该质量模型下，产物分子尽管在吸引型势能面上也优先向前散射。

Figure 4. The PDDCS P₀₀ for the reaction at five different collision energies as indicated in the figure

图4. 在图示5个碰撞能下极化依赖的微分反应截面PDDCSs P₀₀

通过上述研究发现，碰撞能和冲击效应对产物分子的散射方向有直接的影响。为了研究各个矢量空间的分布关联，我们在图5给出了PDDCSS P₂₀随散射角的分布关系。P₂₀是勒让德展开式的第二项 $\langle P_2\left(\text{cos}\theta \right)\rangle$ 的期望值，从图上可以看出它与P₀₀的趋势是相反的。这说明产物角动量优先沿着垂直于k矢量方向极化，即沿垂直于相对速度方向取向。当碰撞能增加时，产物分子的极化程度逐渐变强。P₂₀数值在较高和较低散射角条件下部分呈现正值，而在其它角度范围内，P₂₀数值均为负值。因此P₂₀的数值越小，产物角动量沿垂直于相对速度的方向进行取向的程度越大。

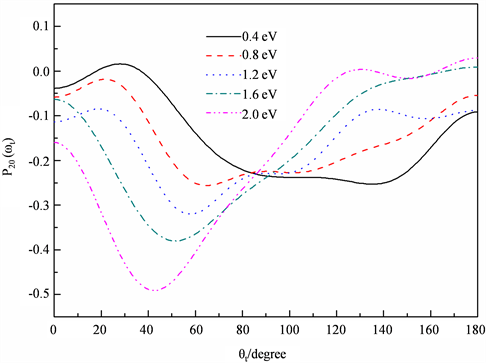
Figure 5. The PDDCS P₂₀ for the reaction at five different collision energies as indicated in the figure

图5. 在图示5个碰撞能下极化依赖的微分反应截面PDDCSs P₂₀

4. 结论

本文在最新高质量从头算势能面上采用准经典轨线理论对 $\text{H}+\text{HS}\to \text{S}+{\text{H}}_{\text{2}}$ 的动力学性质进行了研究。计算的反应几率以及积分截面与量子含时波包方法得到的结果在整个碰撞能范围内吻合的很好。经过数据分析碰撞能在反应碰撞过程中对动力学性质影响较大。计算结果表明碰撞能在低能区能有效促进反应的进行，而在高能区则抑制了反应的进行。计算得到的简单微分散射截面表明产物分子H₂的散射方向在低碰撞能下稍微向侧边和后半球空间散射，而随着碰撞能的增大，冲击效应导致分子主要向前进行散射。产物分子角动量沿垂直于相对速度方向进行取向，且取向程度随碰撞能的增加而增加。本文的计算结果表明该势能面的精度非常高，十分适合利用该势能面进行动力学计算进而揭示该反应的微观机制。反应物的振动和转动激发对动力学性质的影响以及氘原子取代氢原子的同位素效应正在研究中，期待能得到一些有意义的物理图像，并对类似反应的研究提供一些新的思路。

NOTES

^*通讯作者。