1. 前言
随着社会的进步,科技的发展,非线性偏微分方程在物理、数学等学科上的应用越来越广泛,因此也引起了许多数学家的关注。近年来,在许多学者的努力下,提出了许多求解非线性偏微分方程的精确解的方法,例如:Fourier变换 [1] ,三波法 [2] [3] [4] ,可变分离法 [5] 等方法来求解某类非线性偏微分方程的精确解。
本文主要考虑(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程的新精确解。此方程为
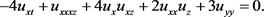 (1)
(1)
在1998年,Song-Ju Yu等人 [6] 将Bogoyavlenskii-Schiff方程 [7]
拓展为一个新的(3 + 1)维非线性演化方程
于是它被称为(3 + 1)维的Yu-Toda-Sasa-Fukuyama (YTSF)势方程,他们随后给出了该方程的行波解。为了方便研究,利用变换
把此方程化为它的潜在形式,也就是本文将要考虑的(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程。
通过扩展的同宿测试法 [8] [9] ,可以获得(3 + 1)维Yu-Toda-Sasa-Fukuyama (YTSF)势方程 [10] 的精确纽结呼吸波解,利用auto-Backland [11] 变换和广义投影的Riccati [12] 方程方法可以得到关于(3 + 1)维YTSF势方程的一些类孤立波子解和非行波解。本文将利用扩展的
展开法 [13] 和新的辅助方程 [13]
(2)
来求解YTSF势方程的一些新精确解的形式。
2. 扩展的
展开法的概述
1) 对于一般的非线性偏微分方程
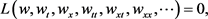 (3)
(3)
其中
是 及关于
的各阶导数的多项式。然后对(3)进行行波变换
及关于
的各阶导数的多项式。然后对(3)进行行波变换
(4)
为待定常数,将(4)代入(3)中,(3)就可化为
(5)
其中
2) 设方程(5)的拟解为
(6)
其中
,
中为待定常数,
可取
,
可通过齐次平衡法求出来,并且
满足以下非线性常微分方程
(7)
其中
为待定常数。
3) 将方程(6)和方程(7)代入方程(5)中,并将
中相同的指数幂的系数合并,令各次幂的系数为零,得到一个关于
,
,
的代数方程组。
4) 利用maple软件求解代数方程组,确定待定常数之间的关系。
5) 通过文献 [13] ,得到5组关于
的表达式
a) 当
且
时,
(8)
b) 当
且
时,
(9)
c) 当
且
时,
(10)
d) 当
且
时,
(11)
e) 当
,
时,
(12)
3. Yu-Toda-Sasa-Fukuyama势方程的新精确解
对方程(1)引入变换(4)
,可将(1)化为方程
(13)
对方程(13)两边进行一次积分得
(14)
其中
为待定常数,由(6)可知
关于
的最高次幂为
,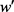 关于
的最高次幂为
,
关于
的最高次幂为
,由齐次平衡法得,最高阶导数线性项
和非线性项
进行平衡,则
,解得
。则(6)的表达式为
关于
的最高次幂为
,
关于
的最高次幂为
,由齐次平衡法得,最高阶导数线性项
和非线性项
进行平衡,则
,解得
。则(6)的表达式为
(15)
将(15)代入(14),得到3组解符合我们(3 + 1)维方程的系数关系
第一组:
第二组:
第三组:
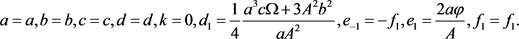
当第一、二、三组解满足
的条件时,
的表达式为
令
(
为不为零的常数),利用maple软件画出部分解的图像,如下:(图1~图3)
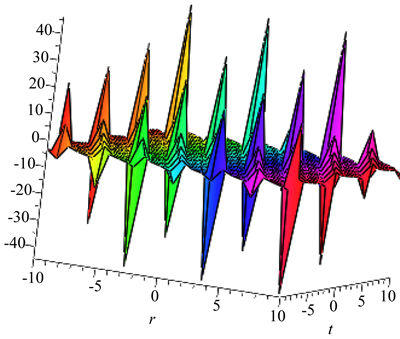
Figure 1. Triangle function solution
schematic diagram
图1. 三角函数求解示意图

Figure 2. Rational partition solution
schematic diagram
图2. 合理分区解示意图

Figure 3. Hyperbolic function solution
schematic diagram
图3. 双曲函数求解示意图
4. 结论
本文通过引用文献 [13] 中扩展的
方法求解(3 + 1)维YTSF势方程的精确解,此方法是把原来
正次幂的形式扩展成
展正负次幂的形式,在此基础上引入新的辅助常微分方程(2)的解的不同形式。通过maple软件确定表达式中待定参数之间的关系,即当方程(2)系数
满足(8)~(12)的关系时,得到了非线性偏微分方程的(3 + 1)维YTSF势方程的新的负幂次形式的精确解,包括双曲函数解、有理分式解和三角函数解的形式,并且此方法还可以用于求解其它非线性偏微分方程。三角函数具有周期性,三角函数解的图像如图1;有理分式的图像如图2所示,由图可以看出此图为中心对称图形;双曲函数是一种类似于三角函数的函数,具有三角函数的一些性质,双曲函数解的图像如图3,是中心对称图像。同时也希望能为大家拓宽解决此类问题的方法。