钢筋混凝土箱型柱塑性铰长度影响因素的试验研究

Experimental Study on Influence Factors of Length of Plastic Hinge of Reinforced Concrete Box Column

摘要: 本文通过对3根轴压比为0.1的钢筋混凝土箱型柱进行低周往复加载试验，探究了横向壁厚比、截面纵筋配筋率这两个因素对塑性铰长度的影响规律，得出以下结论：箱型混凝土悬臂柱在低轴压比时，其塑性铰长度是随着横向壁厚比的增大而增大的；其塑性铰长度是随着构件的纵筋配筋率的增大而增大的。

Abstract: Through doing low cycle reciprocating loading test of 3 reinforced concrete box column under axial pressure ratio of 0.1, the paper explores the transverse wall thickness ratio and cross section of longitudinal reinforcement ratio on the influence law of plastic hinge length, drawing the following conclusions that the plastic hinge length of reinforced concrete box column under low axial compression ratio is increasing with the increase of the ratio of transverse wall thickness and lon-gitudinal reinforcement ratio.

1. 引言

在地震力作用下，桥墩底部会产生较大的弯矩，从而使桥墩底部进入塑性状态进而形成塑性铰，随荷载增加将产生较大的变形直至破坏，而塑性铰长度就是钢筋混凝土柱从柱底沿高度方向的纵筋屈服的长度区域。塑性铰长度是进行结构延性计算和塑性设计的一个重要参数，塑性铰长度越大，则塑性铰区的塑性转动能力越好，即结构的延性越好 [1] [2] [3] [4] 。

关于影响钢筋混凝土箱型柱的塑性铰长因素的研究还不是很全面，目前大多数的研究工作(譬如参考文献 [1] [2] [5] [6] )是在总结了Priestley [7] 和Park [8] 模型的基础上，结合更多的试验结果进行改进，并且研究的重点是集中在实心截面形式的墩柱，而关于箱型柱这种空心截面形式的墩柱塑性铰长度影响因素研究的很少。因此本文通过钢筋混凝土箱型柱的拟静力试验，分析了截面壁厚比和纵筋配筋率对箱型柱塑性铰长度的影响。

2. 试验概况

2.1. 试件设计

本文参考葫芦河特大桥的某一桥墩，取3根编号分为RCBC-1、RCBC-3、RCBC-5的钢筋混凝土箱型柱作为研究对象，有关试件的具体尺寸参数如表1、图1所示。

Table 1. Basic parameters of the specimen

表1. 试件基本参数

2.2. 试验测量内容及方法

试验所使用的设备为四连杆。加载方式采用力与位移混合加载制度，具体的加载过程可以参考文献7中的试验。水平荷载加载前，按设计轴压比计算竖向恒载(3个设计试件均为0.1)并按恒载的50%进行预加载循环俩次后对试件的竖直方向缓慢加载至竖向恒载的100%。水平荷载的加载采用力(荷载)—位移控制的方法：试件开裂前按20 kN/40s逐级加载，开裂后按10 kN/20s逐级加载并循环三次直至屈服，屈服后按屈服位移的0.2倍逐级加载，当极限承载力下降10%~15%时，对试件停止加载 [9] 。加载设备和加载制度如图2所示。

Figure 1. Section size of specimen

图1. 试件截面尺寸

Figure 2. Loading device and loading regime

图2. 加载设备和加载制度

为了探究混凝土箱型柱的塑性铰长度变化规律，试验加载过程中主要测试的内容为荷载位移曲线与纵筋应变。

其中纵筋应变测量方法如下：

在距柱试件根部约1.5 h范围内(h为试件截面高度)的外侧纵筋上粘贴应变片，以测量塑性铰区纵筋应变的变化规律，由此可以通过纵筋应变值计算钢筋混凝土柱的塑性铰长度。纵筋应变片的测点布置见图3 (应变片是对称布置在试件推拉侧)，其中数字标号表示粘贴的纵筋应变片。

3. 试验结果整理与分析

3.1. 确定荷载–位移关系曲线

为了研究构件在低周往复荷载下从屈服到破坏的塑性铰长度变化，通过试验绘制了RCBC-1、3、5柱的荷载–位移曲线见图4，并且在后续分析中分别取图中的相应拐点、最大荷载点和荷载下降至最大荷载85%的点作为构件的屈服点P_y、峰值荷载点P_m、极限位移点P_u [10] 。

本文将选取构件在峰值荷载点和极限位移点时产生的塑性铰长度进行分析。

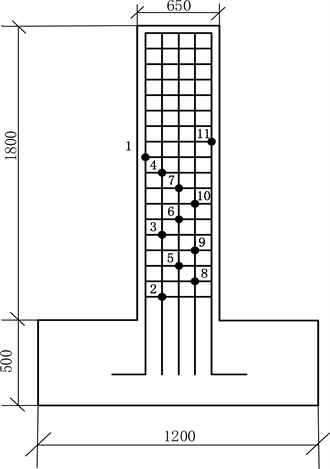
Figure 3. Number and arrangement of steel bar strain gauge for pushed side columns

图3. 受推侧柱试件钢筋应变片的编号和布置

Figure 4. Load-displacement curve

图4. 荷载–位移曲线

3.2. 计算塑性铰长度

作者采用纵筋屈服法来计算3根钢筋混凝土柱的塑性铰长度。

为探究塑性铰长度的发展规律，作者提取了RCBC-1、RCBC-3与RCBC-5从屈服点P_y到峰值荷载点P_m最后达到极限位移点P_u的柱根部1.5 h范围内受拉纵筋应变的测量结果，如图5、图6所示，图中横坐标为受拉纵筋应变，纵坐标为测点距柱根部的距离 [5] 。

由图5、图6可以看出，随着水平荷载的增加，纵筋应变逐渐增大，其增加幅度沿柱高的增加而减小。柱根部第1个应变片(编号为2)的值增加幅度最大，且首先屈服，达到极限位移点时，大部分编号为2的应变片失效，说明应变片被拉坏。从整个变化趋势看，屈服荷载前纵筋应变沿纵向基本呈线性分布，屈服荷载后柱根部纵筋的应变迅速增大，屈服范围逐渐增大。过纵筋屈服应变作直线垂直于横轴，与柱试件在峰值荷载点和极限位移点时的纵筋应变曲线分别产生交点 [5] 。

Figure 5. Curve of longitudinal bar strain along column height of specimens RCBC-1 and RCBC-3

图5. RCBC-1与RCBC-3试件的纵筋应变沿柱高的变化曲线

Figure 6. Curve of longitudinal bar strain along column height of specimens RCBC-1 and RCBC-5

图6. RCBC-1与RCBC-5试件的纵筋应变沿柱高的变化曲线

具体计算步骤如下：

1) 计算纵筋的屈服应变 ${\epsilon }_y=\frac{{\sigma }_y}{E}=\frac{\text{335N}/{\text{mm}}^{\text{2}}}{\text{20}\times {\text{10}}^{\text{5}}\text{N}/{\text{mm}}^{\text{2}}}=1.675$ ，取1675 $\mu \epsilon$ 。

2) 以RCBC-1与RCBC-5试件为例，在图6中过纵筋屈服应变作直线垂直于横轴，分别与纵筋应变曲线交于点A、B、C、D，这四个点对应的纵坐标即为该荷载作用下的塑性铰长度 [6] 。

在分析截面壁厚比这一影响因素时，作者选取RCBC-1与RCBC-3试件作为研究对象。通过上述计算塑性铰长度的方法，可以整理得到RCBC-1与RCBC-3试件的塑性铰长度，见表2。

Table 2. Plastic hinge lengths of RCBC-1 and RCBC-3 specimens

表2. RCBC-1与RCBC-3试件的塑性铰长度

注：低周往复加载试件的塑性铰长度取推、拉两侧的平均值。

在分析纵筋配筋率比这一影响因素时，作者选取RCBC-1与RCBC-3试件作为研究对象。通过上述计算塑性铰长度的方法，可以整理得到RCBC-1与RCBC-5试件的塑性铰长度，见表3。

Table 3. Plastic hinge lengths of RCBC-1 and RCBC-5 specimens

表3. RCBC-1与RCBC-5试件的塑性铰长度

注：低周往复加载试件的塑性铰长度取推、拉两侧的平均值。

3.3. 塑性铰长度的影响因素及分析

为探究影响塑性铰长度的因素，本文对3根箱型柱进行试验后得到其塑性铰长度，主要是探究截面横向壁厚比、纵筋配筋率对塑性铰长度的影响规律。

3.3.1. 截面壁厚比变化对塑性铰长度的影响

选取试件RCBC-1与RCBC-3进行对比分析，得到横向壁厚比变化对塑性铰长度的影响，各参数列于表4所示。

Table 4. Related parameters of each column section and plastic hinge length

表4. 各柱截面相关参数及塑性铰长度

1) 当轴压比为0.1时，RCBC-3试件相比于RCBC-1试件的横向壁厚比增加了40.9%，相应的峰值荷载点与极限位移点的塑性铰长度分别增加了0.89%、16.07%，说明提高构件的横向壁厚比对荷载加载前期的塑性铰长度影响较小，但是当构件趋于破坏时，对塑性铰长度影响比较大。这是由于受压柱在低轴压比下，其斜截面受剪承载力相对较低，因此构件主要是受剪破坏的，增大箱型柱的腹板面积可以大大提高其抗剪强度，从而提高试件的延性，这对塑性铰的生成是很有利的。

2) 从表4中可以看出钢筋混凝土箱型柱在低轴压比下，塑性铰长度在加载前期受横向壁厚比影响较小，但随着荷载逐渐增大，塑性铰长度受横向壁厚比影响较大，且随着横向壁厚比的增大而增大。

3.3.2. 纵筋配筋率变化对塑性铰长度的影响

选取试件RCBC-1与RCBC-5进行对比分析，得到纵筋配筋率变化对塑性铰长度的影响，各参数列于表5所示。

Table 5. Related parameters of each column section and plastic hinge length

表5. 各柱截面相关参数及塑性铰长度

1) 当轴压比为0.1时，RCBC-5试件相比于RCBC-1试件的纵筋配筋率增加了29.1%，相应的峰值荷载点与极限位移点的塑性铰长度分别增加了17.0%、22.5%，这是由于在给构件施加较小的轴压比时，箱型柱的破坏主要是由纵筋控制，当增加构件的纵筋配筋率时，有利于塑性铰的形成。

2) 从表5中可以看出钢筋混凝土箱型柱在低轴压比下，箱型柱的塑性铰长度随着其纵筋配筋率的增加而增大。

4. 结论

本文以3个试验对象为基础，分析了壁厚比、纵筋配筋率这两个因素对塑性铰长度的影响，塑性铰的形成可以提高桥梁在受到地震作用时的耗能大小，并提高箱型截面桥墩的延性，这对桥梁的抗震性能研究有着重要的意义。

1) 在低轴压比下，钢筋混凝土箱型柱的塑性铰长度在加载前期受横向壁厚比影响较小，但随着荷载逐渐增大，塑性铰长度受横向壁厚比影响较大，且随着横向壁厚比的增大而增大。

2) 钢筋混凝土箱型柱在低轴压比下，箱型柱的塑性铰长度随着其纵筋配筋率的增加而增大。

3) 在低轴压比下，可以适当的增加箱型柱的壁厚比和纵筋配筋率来提高箱型柱的抗震性能。

参考文献

NOTES

^*通讯作者。