1. 引言
本文中考虑三角形区域上如下椭圆型方程
(1.1)
其中
为三角形区域,
,以及
,
均为给定的光滑函数,n表示沿着边界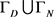 的单位法向量。
的单位法向量。
近年来,最小二乘有限元由于其结合了混合有限元法的优点已经被应用于流体力学领域中,如Stokes方程和Navier-Stokes方程等的数值求解 [1] [2] 。该方法的优点是可以避免Ladyzhenskaya-Babuška Brezzi (LBB)稳定性条件,所以等阶的插值多项式可用于所有变量,且所离散得到代数方程的系数矩阵具有对称正定的特点 [3] 。在求解时便于利用合适的迭代方法,如共轭梯度法等。为了得到高阶精度方法,有部分学者发展偏微分方程的最小二乘谱方法。文 [4] 中提出了椭圆型边值问题的拟谱最小二乘法,但是对于Chebyshev情况误差估计受其权函数影响而得不到最优。文 [5] 则研究耦合Legendre与Chebyshev方法且数值分析中避免了Chebyshev权函数的影响从而得到最优的误差估计。最小二乘拟谱方法还被应用于流体力学领域中Stokes方程的数值求解 [6] 。
谱方法由于其对于光滑解的偏微分方程有高阶谱精度,因此它与有限元法和有限差分法等一起成为偏微分方程重要的数值解法 [2] 。近年来,谱方法和拟谱方法被广泛应用于各领域数理模型的计算,如Navier-Stokes方程 [7] 和Fokker-Planck方程 [8] 等等。为了克服经典谱方法对矩形区域的依赖,基于Duffy’s三角形映射,文 [9] [10] 中发展了三角单元谱方法。文 [11] 中通过引进新的三角形映射研究了问题(4.4)的三角谱方法。该映射提供均匀的网格点映照 [12] [13] ,基于该映射,在 [13] 中考虑了三角单元谱元法,并在 [12] 中研究了相应的逼近理论与构造椭圆方法的三角谱元法。近年来,文 [14] 研究了耦合三角单元和矩形元谱元法。文 [15] 发展了椭圆方程和Stokes方程的三角谱元法且推广到三棱柱谱方法 [16] 。本文中利用文 [11] 的三角形映射,我们研究椭圆方程(4.4)的最小二乘三角单元Legendre Galerkin数值积分(LST-LGNI)解法。
2. 记号与三角形映射
对于任意非负整数s,设
为经典的Sobolev空间,其中
和
分别表示范数和半范数。当
时,则
,且
和
分别为它的内积与范数
。为了简单起见,记
对于任意的
,文 [11] 中给出了
到
的一个新型映射T:
(2.1)
令
,则T的逆映射
:
如文 [11] 中得到Jcobian为:
。因此,可定义内积为:
或者
(2.2)
文 [11] [13] 指出:由(2.2)得到若
在
的斜边中点
存在,则经过变换后有
(2.3)
设
其中
表示
次数不超过N多项式空间。因此,有限维空间可定义为:
(2.4)
设
和记
上与
对应的有限维空间为
。文 [11] [13] 定义拟插值
为
(2.5)
其中
,但
则由
所确定和
是
在上与LGL配置点对应的点。
3. LST-LGNI格式
引进通量
则
其中
,n和
分别对应边界
的单位法向量和单位切向量。如文 [1] 得到一阶方程组为
(3.1)
其中边界条件为
设
定义系统(3.1)在
范数下的最小二乘函数为:
(3.2)
其中
。即,对应的最小值问题为:求
满足
因此,上述对应的变分格式为:求
满足
(3.3)
其中
设
为三角形区域
上对应有限维空间
的所有次数不超过N多项式的空间。设
(3.4)
最小二乘函数(3.2)离散形式为:
其中
,
为Legendre-Gauss-Lobatto (LGL)插值算子,或者Chebyshev-Gauss-Lobatto (CGL)配插值算子。
类似地,得到离散的最小问题为:求
使得
(3.5)
因此,最小二乘三角形Legendre Galerkin数值积(LST-LGNI)格式为:求
使得
(3.6)
其中
4. 数值算例
为了验证格式(3.6)的谱精度和有效性,本节给出一些数值算例且与一些三角单元谱方法进行比较。下面定义离散的
误差为:
其中
和
分别为LGL节点和其对应的数值积分权函数。
例4.1:考虑问题(4.1),
,以及
。精确解为
(4.1)
(4.2)
文 [17] 中采用Chebyshev配置方法对该算例进行计算,这里则用LST-LGNI (3.6)计算。表1中分别给出了文 [18] 和我们的格式(3.6)的关于L2-范数的数值误差,其中误差的定义为
以及
。数值结果表明,该方法具有高阶谱精度且文 [18] 中给出的数值结果类差不多。

Table 1. Error in L2-norm for example 4.1
表1. 例4.1中的L2-范数误差
例4.2:考虑问题(4.4),其中
。精确解分别为(4.1)和图1中给出了最大值点误差和离散的L2-误差且数值结果显示误差具有高阶谱精度。表2中给出数值表明该方法的谱精度优于 [19] 方法。

Figure 1. Maximum point error and L2-norm error; On the left hand side: Error of the exact solution (4.1), on the right hand side: Error of the exact solution (4.3), where
,
图1. 最大值点误差和L2-范数误差。左侧:精确解为(4.1)的误差情况;右侧:精确解(4.3)的误差情况,其中
和
例4.3:考虑问题 [11]
(4.4)
精确解如文 [11] 中给出为

Table 2. Error in L2-norm for example 4.2
表2. 例4.2中的L2-范数误差
(4.5)
为了验证我们的方法LST-LGNI (3.6)对变系数为多项式情况也是有效的。在该算例中将我们的数值结果与文 [11] 的三角形Legendre谱方法的进行比较。表3中分别给出文 [11] 中三角谱方法与LST-LGNI (3.6)的数值结果。由此注意到格式(3.6)谱精度比 [11] 中给出的要稍好一些。

Table 3. Error in L2-norm for example 4.3
表3. 例4.3中的L2-范数误差
5. 总结
本文研究了最小二乘Legendre Galerkin的数值积分的方法。该方法结合最小二乘,离散时采用Legendre Galerkin数值积分处理,使得格式计算方便且导出的代数方程系数具有对称正定的特点,求解时允许采用如共轭梯度法。数值实验验证该方法具有高阶谱精度。更有意义是考虑复杂区域上的微分方程的求解,类似文 [14] 进一步将结合三单元与矩形元发展高效的最小二乘谱元格式。
基金项目
国家自然科学基金资助项目(No.11701119),大学生创新训练资助项目(No.201710595033),广西自然科学基金资助项目(No.2017GXNSFBA198053),广西混杂计算与集成电路设计分析重点实验室开放课题资助(No.HCIC201607)。
参考文献
NOTES
*通讯作者