CT系统参数标定及成像研究

Study on Parameters Calibration and Imaging of CT System

摘要: CT系统安装时存在的误差在一定程度上影响到样品的成像质量，本文提出了一种借助已知结构模板对CT系统进行参数标定后再对未知结构样品进行成像的方法。首先，借助已知结构的模板及其X射线接收信息，基于卷积逆投影图像重建方法讨论了一种已安装好的典型二维CT系统的主要参数标定；然后利用已获得的标定参数，建立基于图像灰度的吸收率计算模型，研究未知结构的样品成像问题；最后对影响标定精度和稳定性的误差因素进行分析，设计新模板以改进标定精度和稳定性。本文的研究对降低CT系统安装误差影响、提高样品成像质量具有一定意义。

Abstract: The errors arising during installation of CT system will affect the imaging quality of the samples to some extent. In this paper, a method is proposed to image the unknown structure samples by cali-brating the parameters of CT system with the known structure template. Firstly, based on convo-lution inverse projection method for image reconstruction, we discuss the main parameters cali-bration of a typical two-dimensional CT system with the help of the known structure template and its X-ray receiving information. Then, based on the obtained calibration parameters, a model for calculating the absorptivity based on image gray level is established to study the imaging problem of unknown structure samples. Finally, the error factors affecting accuracy and stability of the calibration are analyzed, and a new template is designed to improve accuracy and stability. The research in this paper has a certain significance to reduce the influence of CT system installation error and improve the imaging quality of the sample.

1. 引言

计算断层摄影(Computed Tomography)，简称CT，是电子计算机和X线相结合，应用到医学领域的重大突破，它使传统的X线诊断技术进入了计算机处理和图像显示的新时代 [1] [2] 。随着CT系统的应用日渐广泛，它可以在不破坏样品的情况下，利用样品对射线能量的吸收特性对生物组织和工程材料的样品进行断层成像，由此获取样品内部的结构信息。然而，CT系统在安装时往往存在误差，从而影响成像质量 [3] 。针对这一问题，本文首先基于一种典型的二维CT系统，借助已知结构的模板(即样品)及其X射线接收信息研究CT系统主要参数的标定，包括CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向；其次，基于已获得的标定参数，讨论未知结构的样品成像问题；最后，对影响标定精度和稳定性的因素进行分析，并设计新模板以改进标定精度和稳定性。

2. CT系统主要参数标定

文中使用的二维CT系统如图1所示 [3] ，平行入射的X射线垂直于探测器平面，每个探测器单元看成一个接收点，且等距排列。已知结构的模板几何信息如图2所示 [3] 。

Figure 1. Two-dimensional CT system schematic diagram

图1. 二维CT系统示意图

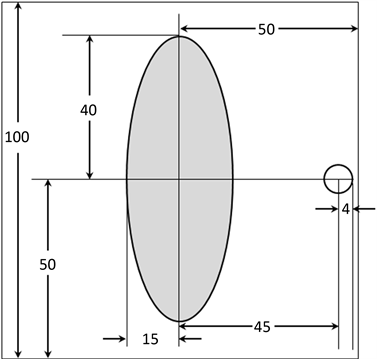
Figure 2. Geometric information of known structural templates

图2. 已知结构模板的几何信息

2.1. 探测器单元间距的计算

对文献 [3] 附件2的模板接收信息，根据吸收率的强弱进行染色，得到512个探测单元旋转180个方向的接收结果，见图3。

Figure 3. Absorption chromatogram

图3. 吸收率色阶图

分析图3中吸收率可知，当系统旋转到A处时，X射线与圆、椭圆相切，并在下一次旋转时与二者相离；B处吸收率最强而范围最小，此时X射线应最接近平行于椭圆长轴；C处接收范围最大而强度除去中间深色圆形的叠加后是最弱的，此时X射线应最接近平行于椭圆短轴，三种情况如图4中所示。

探测器单元间距公式为： $\Delta d=l/n$ ，其中l为n个连续探测器的总间距。

按照图4的分析，对文献 [3] 附件2中的数据进行比对，得：

$n_A\approx 29$ ， $l_A=8\text{mm}$

$△d_A=\frac{8}{29}\text{mm}\approx 0.2759\text{mm}$

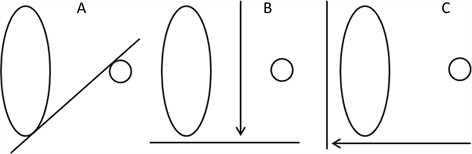
Figure 4. X-ray scanning at three positions

图4. ABC三处射线扫描情况

考虑到旋转可能跳过平行于长轴或短轴的方向，对B、C附近几组数据进行比对发现，数据之间变化很小，可认为系统转到此两处时近似经过两轴，得：

$n_B\approx 109$ ， $l_B=30\text{mm}$

$△d_B=\frac{30}{109}\text{mm}\approx 0.2752\text{mm}$

$n_C\approx 289$ ， $l_C=80\text{mm}$

$△d_C=\frac{80}{289}\text{mm}\approx 0.2768\text{mm}$

由于C处采集的数据较多，认为该处数据能更合理的反映探测单元间的实际距离，因此得到最终结果为0.2768 mm。

2.2. 卷积逆投影图像重建

逆投影是指各个方向的投影逆向返回到该方向的位置，如果对多个投影方向中的每个方向都进行这样的逆投影，就可以建立平面上的一个部分，典型的方法是卷积逆投影重建 [4] 。

卷积可看成一种滤波手段 [5] ，卷积逆投影相当于先对数据滤波再将结果逆投影回来，可以使模糊得到校正。而卷积重建法是一种变换重建法，可以根据傅里叶变换推出 [6] 。

图像函数 $f\left(x,y\right)$ 的二维傅里叶变换为：

$F\left(u,v\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }f\left(x,y\right){\text{e}}^{-j2\text{π}\left(ux+vy\right)}\text{d}x\text{d}y}}$

逆变换公式为：

$f\left(x,y\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }F\left(u,v\right){\text{e}}^{j2\text{π}\left(ux+vy\right)}\text{d}u\text{d}y}}$ (1)

用 $u=r\cos \theta ,v=r\sin \theta$ 进行代换，得公式(1)的极坐标形式：

$f\left(x,y\right)={\displaystyle {\int }_0^{\text{2π}}{\displaystyle {\int }_0^{\infty }F\left(r,\theta \right){\text{e}}^{j2\text{π}\left(x\cos \theta +y\sin \theta \right)}r\text{d}r\text{d}\theta }}$

由傅里叶变换共轭对称性得：

$f\left(x,y\right)={\displaystyle {\int }_0^{\text{2π}}{\displaystyle {\int }_0^{\infty }F\left(r,\theta \right){\text{e}}^{j2\text{π}\left(x\cos \theta +y\sin \theta \right)}\left|r\right|\text{d}r\text{d}\theta }}$ (2)

令 $f^{\prime }\left(x,y,\theta \right)={\displaystyle {\int }_{-\infty }^{\infty }{\text{e}}^{j2\text{π}\left(x\cos \theta +y\sin \theta \right)}F\left(r,\theta \right)\left|r\right|\text{d}r}$ ，公式(2)等价于：

$f\left(x,y\right)={\displaystyle {\int }_0^{\text{π}}{f}^{\prime }\left(x,y,\theta \right)\text{d}\theta }$ (3)

当r取 $\left(-1/2d,1/2d\right)$ 时，公式(2)近似为：

$f\left(x,y\right)\approx {\displaystyle {\int }_0^{\text{π}}{\displaystyle {\int }_{\frac{-1}{2d}}^{\frac{1}{2d}}F\left(r,\theta \right){\text{e}}^{j2\text{π}\left(x\cos \theta +y\sin \theta \right)}\left|r\right|\text{d}r\text{d}\theta }}$

即：

$h\left(\rho \right)={\displaystyle {\int }_{\frac{-1}{2d}}^{\frac{1}{2d}}\left|r\right|{\text{e}}^{j2\text{π}\rho }\text{d}r}$ (4)

联立公式，经化简得：

$f^{\prime }\left(x,y,\theta \right)={\displaystyle {\int }_{-\infty }^{\infty }g\left(\rho ,\theta \right)h\left(x\cos \theta +y\sin \theta -\rho \right)\text{d}\rho }$ (5)

由化简结果知，可以先将投影数据 $g\left(\rho ,\theta \right)$ 和相应脉冲滤波器(公式(4))进行卷积，然后用公式(3)对不同旋转角θ求和，就能实现图像重建。

本文利用Matlab函数进行卷积重建，还原探测器视角的扫描图像，将图像二值化，编程算出图像的中心点、椭圆的中心并建立坐标系，如图5所示。

Figure 5. Restoring image to establish coordinate system

图5. 还原图像建立坐标系

图中G点为图像正中心，由旋转平移的性质知，原系统旋转中心坐标相当于G点在图5坐标系中的坐标。这里我们设图5的左下角顶点为坐标原点。

先将复原图比例调整为与文献 [3] 附件1中一致。

la是经过椭圆心、圆心的直线，lb为椭圆长轴。原图中，椭圆长短轴的交点、圆心的位置是已知的，计算两线的方程为：

$\text{la}:y=-0.5677x+258.0935$

$\text{lb}:y=1.7613x-204.6182$

联立解得旋转中心为(−9.0663, 6.3578)。

2.3. 平面投影角度计算模型

求解CT系统X射线的180个方向，关键在于确定每个时刻X射线相对于椭圆心、圆心连线的夹角，为此，本节建立了基于平面几何投影的角度计算模型。

Figure 6. Centroid distance projection model

图6. 圆心距投影模型

在利用投影计算方向之前，文中选取了部分只穿过椭圆的X射线，对它们的接收强度与它们穿过椭圆的长度进行拟合，发现二者之间呈线性相关，关系式如下：I = 1.7722L。

在图6中，AB为某时刻探测器相对位置，A、B分别为椭圆心O₁、圆心O₂经X射线在探测器上的投影，可知：∆CAO₁~∆CBO₂，则有 $\frac{\left|\text{CA}\right|}{\left|{\text{CO}}_1\right|}=\frac{\left|\text{CA}\right|+\left|\text{AB}\right|}{\left|{\text{CO}}_1\right|+\left|{\text{O}}_1{\text{O}}_2\right|}$ ，化简得： $\frac{\left|\text{CA}\right|}{\left|{\text{CO}}_{\text{1}}\right|}=\frac{\left|\text{AB}\right|}{\left|{\text{O}}_{\text{1}}{\text{O}}_{\text{2}}\right|}=\cos \alpha$ 。

|O₁O₂|已知，AO₁、BO₂分别经过椭圆心、圆心，由前述线性相关性，得出这两条X射线应是穿过椭圆和圆的射线中接收强度最大的两条，因此通过筛选出文献 [3] 附件2中每列经过椭圆的射线接收强度最大值和经过圆的射线接收强度最大值，就可找到每次旋转后的AO₁和BO₂，两线间距离为投影|AB|，从而可得 的值。

利用Matlab拟合出的余弦函数为： $\cos \alpha =-0.0093+0.9926\ast \cos \left(0.0175t+0.4807\right)$ ，相关度信息为：R-SQUARE = 0.9995，RMSE = 0.0141，表明拟合效果较好。

求反函数拟合得到180次旋转的角度变换公式为： $P=1.0015t+28.1355+90$ ，单位为度。

由上式可计算出X射线在以椭圆心为原点的坐标轴中的初始方向，见图7。

Figure 7. Initial direction of X-ray

图7. X射线初始方向

因此，CT系统使用的X射线的180个方向如表1所示(单位为度)。

Table 1. 180 Directions of X-ray

表1. X射线的180个方向

3. 未知结构样品成像研究

3.1. 图像的重建和位置还原

文献 [3] 附件3是利用上述CT系统得到的某未知样品的接收信息，利用MATLAB函数卷积重建还原探测器视角的扫描图像，得到该未知样品的几何形状如图8所示。

Figure 8. Shape reconstruction of sample

图8. 样品形状重建

由于系统X射线初始角度为119.1370˚，为计算样品在托盘中的位置，文中用MATLAB函数将样品绕旋转中心逆时针旋转29.1370˚。

又因为旋转后得到的图形大小为362 * 362像素，而托盘图像大小为256 * 256像素，应进行裁剪，所以取以距原图像中心以左(9.0663/100) * 256像素、以上(6.3578/100) * 256像素为中心的256 * 256像素的空图像矩阵对原图进行裁剪，得到样品在托盘中的位置如图9所示。

Figure 9. Position of sample on pallet after cutting, rotating and translating

图9. 裁剪旋转平移后样品在托盘上的位置

3.2. 基于图像灰度的吸收率计算模型

图10为文献 [3] 附件1中样品吸收率的色阶图，由该图可知，托盘上放置样品的地方吸收率为1，其余地方吸收率为0。

Figure 10. Absorption chromatogram of annex 1

图10. 附件1中吸收率色阶图

图11为文献 [3] 附件2中图像重建后的灰度矩阵图像：

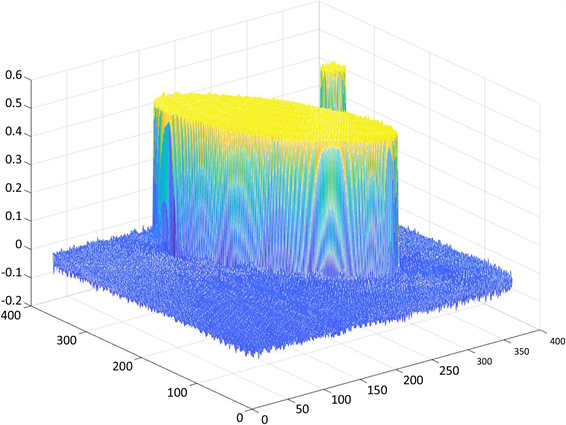
Figure 11. Gray matrix after image reconstruction of annex 2

图11. 附件2中图像重建后的灰度矩阵图

忽略为还原样品位置处理图像时产生的噪点，观察矩阵值发现该样品所在位置对应像素点的灰度值均相同，可得出以下结论：某一点的吸收率是关于该点像素灰度值的相对值，并将灰度值最大的像素点对应位置的吸收率设为1，其余像素位置吸收率均以该像素为基准进行等比例缩小，得到吸收率计算模型：

$\{\begin{array}{l}{\alpha }_{\left(i,j\right)}=\delta \ast g_{\left(i,j\right)}\\ \delta =1/{\left[g_{\left(i,j\right)}\right]}_{\max }\end{array}$

其中 $$ 为矩阵第i行第j列像素对应位置的吸收率，δ为将最大灰度值标准化为1的比例， $g_{\left(i,j\right)}$ 为矩阵第i行第j列像素的灰度值。

根据吸收率计算模型公式对文献 [3] 附件3重建图像的灰度矩阵进行标准化运算，得到的新矩阵每个元素的值即为该点像素对应位置的吸收率，标准化之后的图像如图12所示，与图9相比灰度变化较明显。

Figure 12. Standardized gray image

图12. 标准化后的灰度图像

4. 标定精度及稳定性

4.1. 影响因素分析

影响标定精度和稳定性的因素主要包括以下三点：

1) 标定探测器相邻单元之间距离时的误差。

本文通过计算椭圆长轴长度与椭圆长轴所跨单元数量之间的比值来近似确定探测器相邻单元之间的距离。相比于采用圆的半径、椭圆短轴来计算的方法，该方法可获得更高的精度。但是，无论采用哪种方法，图形的边缘都不可能正好对准探测器单元，因此，在计算过程中将出现不可避免的误差。采用尽可能大的图形来做计算只能尽可能缩小这一偏差在最终结果中的比例，不能彻底消除误差。

2) 计算探测器各个时刻位置时的误差

文中利用椭圆心和圆心的距离及其在CT探测器上的投影距离的比值来获得探测器各个时刻相对于x轴的倾斜角。这一方法在椭圆和圆在探测器上的投影重叠时，将无法推导出探测器的精确方位，只能凭借函数的特征来拟合出探测器的当前位置。在高精度要求的场合，这将引起接下来旋转中心计算的偏差甚至重建图像的畸变。

3) 确定重建图像和原图之间关系时的误差

重建图像可以被大体视为原图经过旋转、平移和缩放后的结果，其中旋转和缩放都可能引起图像失真 [7] 。文中采用双三次插值 [8] 来尽可能保证图像画质不退化。但是由于图像是由矩阵来表示的，每一次处理过程中数据的舍入都会产生一定的误差，而总的误差会在这些误差的叠加当中被放大。其中y轴的位置并不能由数据直接得到，而需要通过旋转中心和x轴的位置来推导，这将导致2)中有关倾斜角和旋转中心的误差在后面的计算中被放大。

4.2. 新模板设计

针对上述误差，为改进标定精度和稳定性重新设计模板如图13、图14所示：

Figure 13. Template for first calibration

图13. 第一次标定用的模板

将标定过程分为两个阶段。在第一阶段使用图13的模板，模板中有且仅有一个椭圆，避免了图形重合的现象，完整地获取180个射线方向(而不是通过函数模拟)，从而精确计算CT系统旋转中心和重建图像的倾斜角度。第二阶段使用图14的模板，该模板在原来椭圆的基础上，在x轴上和y轴上分别增加一个正圆。这样能精确确定x轴和y轴的位置，并能获得更为精确的重建图像和原介质的比例尺。但是，这种做法将造成额外的一次扫描，增大了标定过程的成本。

另外，由于更大的图形能够在一定程度上减小离散图形带来的误差，因此，本文决定采用比原来模板更大的图形来进行标定。但图形也不能无限放大，要保证托盘能够放置样品且样品能够被扫描到。

5. 结束语

本文在计算相邻探测器距离以及射线各个时刻方向的时候，将原问题抽象为几何模型，极大地降低

Figure 14. Template for second calibration

图14. 第二次标定用的模板

了解题难度和运算量。为了快速方便地重建投影图像并寻找CT系统旋转中心，文中采用了卷积法，使得重建后的图像具有较高的精确度和还原度。利用MATLAB命令对图像进行旋转、裁剪、平移等处理过程中双三次插值等方法的运用最大程度上避免了图像失真问题。通过对参数标定过程中的不精确和不稳定因素的分析，本文对症下药，设计了一种新的标定模板。对标定参数的精确性和稳定性的进一步探讨是今后研究的内容。

基金项目

云南大学教育教学改革研究项目(2017Y13)。

参考文献