1. 引言
极端降水事件给人们的生产、生活及财产造成了重大影响和损失,如6.30长沙特大暴雨、7.16北京暴雨,但同时也促进了极值分析领域的发展 [1] 。IPCC报告指出气候变暖导致世界上绝大多数地区暴雨频率、强度有所增加 [2] 。因此极端气候下的防灾问题受到了人们的广泛关注 [3] [4] 。进行极端降水事件的估计,对洪涝规划与工程设计具有重要的意义。
传统的极值模型 [1] 有广义极值分布(GEV)与广义帕累托分布(GPD),GEV用来拟合块最大值或者块最小值,但由于需要的样本量很大,不太适用于缺乏数据的地区。广义帕累托分布(GPD)可以根据选定的阀值来扩大样本量,从而有效的利用了较大降雨量,因此收到了更为广泛的应用 [5] [6] 。
本文基于GEV分布来拟合日本广岛地区30年的降雨数据。但由于广岛的降雨量具有较强的非平稳性,所以将采用季度模型来进行模拟,最后通过北野 [7] 提出的经验度理论,对各季节的模型做最大外推年限的试算,其结果可为国内的洪涝治理与工程设计提供科学有效的参考。
2. 研究方法
2.1. 泊松分布与极值分布
已知n年的日最大降雨量数据,其中日降雨量超过y mm的共有0个,根据泊松分布:
(1)
(2)
其中
是n年最大值的概率分布函数;
为每n年降雨量超出y mm的数据个数。当n取1时,式1为GEV分布函数。
对GPD分布函数 [8] :
(3)
其中u为阀值。当降雨量y超过u时,该降雨量可被视为极值数据。
即为GPD分布函数。
2.2. Delta估计
假定
为一标量函数,
为GEV分布的参数
极大似然估计值,那么有如下的公式:
(4)
(5)
(6)
其中式(4)表明标量函数
的估计值服从均值为
,方差为
的正态分布。
为
的方差协方差矩阵,计算时均以估计值代入,此方法即为delta法。
2.3. 季度模型
对于非平稳的数据,可采用以下的非平稳的GEV模型来进行研究:
(7)
但从长期角度来看,一个地区的降雨模式,气候是较为稳定的,所以假定模型的尺度参数与形状参数不变,而本文中的降雨数据受季风与夏秋季的台风影响,所以降雨量具有较为明显的差别,故本文采用以下的非平稳GEV模型:
(8)
2.4. 似然比检验
本文将使用似然比检验进行季度模型适合与否的检验,似然比检验的原理 [1] 如下所示:
假设较为简单的模型
是较为复杂的模型
的子模型(本文中季度模型为
),它们各自的对数似然函数值为
、
,令
,此时的D服从卡方分布。当
(
为卡方分布的
的分位数)时,此时较为复杂的模型
更符合实际。
2.5. 模型检测
对最终的模型需要做模型拟合度的检测,常用非参数的检测方法包括pp图、qq图检测,但是对于非平稳模型的pp图、qq图,我们将式8代入下式 [1] :
(9)
此时
近似的服从标准的Gumbel分布。pp图和qq图上的点分别通过下式计算:
(10)
(11)
2.6. 经验度试算
北野 [7] 通过经验度的计算,得出当经验度K小于2时,模型的结果较为可信,下面是经验度的公式:
(12)
其中
为泊松分布的发生率,及单位时间内事件发生的歌,由公式的形式可知经验度K的倒数与变异系数的平方形式一样,但是并不能由变异系数代替,这是因为
为泊松分布的发生率的前提是伽马分布为贝叶斯估计的自然共轭分布,经验度的具体计算方法请参阅文献 [7] 。
3. 实例应用
3.1. 模型拟合
本文选取日本广岛市1985~2014年的日最大雨量值进行分析。基于日本气象厅发布的历年台风数据 [9] ,广岛相对于日本偏北部的城市所受台风影响较多,降雨数据较为不平稳。
广岛市位于日本本州西部,属亚热带湿润气候,冬季凉爽至温和,夏季炎热潮湿。与日本大部分地区一样,夏季的温度稍稍滞后于夏季的时令。冬季是最干燥的季节,但降水事件也比较频繁。降雨在6月和7月达到高峰,另外由于夏季的台风影响,暴雨事件也频繁发生。因为全球性的气候变暖,全球暴雨事件的不稳定,有必要加深对极端降雨事件的理解,本文采用GEV分布进行模型拟合。下图1为30年各季节月最大日降雨量。


Figure 1. Maximum daily rainfall of every month in different seasons
图1. 不同季节月最大日降雨量
从图中可以看出,夏秋季节,雨量值偏大,春冬季节雨量值较小,但考虑到模型的实用性,模型并不是越复杂越好,所以本次模型假设:
(9)
(10)
不考虑季节模型时,估计值为:
≈ 8.06/mm (0.37),
≈ 5.83/mm2 (0.32),
≈ 0.35/mm (0.06),括号内为标准差,由delta法计算得到。模型的对数似然函数值为−1273.54。
考虑季节模型时,估计值如下表1所示:

Table 1. Estimation of seasonal model parameters
表1. 季节模型参数估计值
注:括号内为标准差。
季节模型的对数似然函数值为−1227.35。季节模型比一般模型多了二个参数,于是有以下的结果:
(11)
因此此时较为复杂的季节模型更能拟合广岛地区的降雨数据。
由式(10)、(11)计算得到的模型诊断图如下所示:
图2为pp图与qq图,它们都近似为直线,说明模型的拟合效果较好。
 (a) 概率图
(a) 概率图  (b) 分位数图
(b) 分位数图
Figure 2. Model check plot
图2. 模型诊断图
3.2. 经验度计算
经验度随重现期变化的曲线以及相应经验度小于2的重现水平曲线分别如图3和图4所示:
 (a)
(a)  (b)
(b) 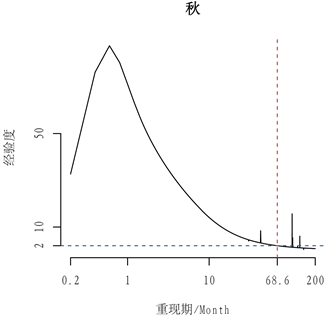 (c)
(c)  (d)
(d)
Figure 3. Degree of experience curve
图3. 经验度曲线
 (a) 春
(a) 春 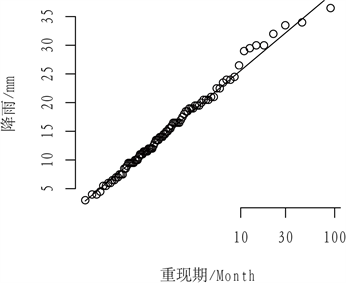 (b) 夏
(b) 夏 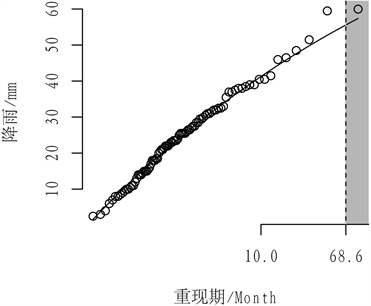 (c) 秋
(c) 秋  (d) 冬
(d) 冬
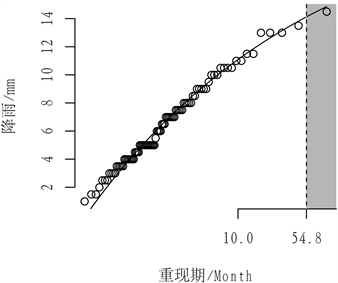
Figure 4. Return level curve
图4. 重现水平曲线
图3显示,经验度随着重现期的增大而减小,图(a)中显示,当重现期大于54.2个月时,经验度开始小于2,这说明基于30年(乘以春季3个月) 90个月的降雨数据,最大的外推重现期为54.2个月。图(b)、(c)分别为68.6、84.6个月。而图(b)中经验度始终大于2,这可能是由于近似计算的原因,在进行试算后,得知夏季的降雨分布近似为Gumbel分布,所以,我估计它的形状参数为0,具有一定的误差。图中数据的波动,是由于数据量较少造成的。
图4中的空心点为90组的季度日最大降雨量值;曲线是基于90组数据得到的回归模型;(a)、(c)、(d)中的灰色区域表示,当数据的重现期分别大于54.2、68.6、84.6个月时,经验度K小于2。由此对应的横坐标,即为基于已有的降雨数据,所能得到的最大重现期的重现水平值。
4. 结论
本文基于日本广岛地区30年的日最大降雨量数据,进行季度模型的计算,通过似然比的检测得出,季度模型能有效的提高模型拟合的优度。然后我们进行了最大外推重现期的计算。通过经验度的计算,我们得出春季重现期在54.2个月内的外推是比较可信的,相应的秋季与冬季的最大外推重现期为68.6、84.6个月。夏季的结果不太准确,是由于Gumbel分布的近似计算造成的。后期的工作中应该针对Gumbel分布找出合适的经验度计算方法。模型中考虑降雨数据的不均匀性可以有效地提高模型拟合的优度。经验度的计算简单直接,能够明确的给出外推的极限,可为防洪,工程设计提供决策参考。
NOTES
*通讯作者。