1. 引言
人的面部表情向来都是神秘而复杂的,就像世界名画《蒙娜丽莎的微笑》一样,但同时,人们对于面部表情的探索也从未止步。目前在计算机领域一个非常热门的课题就是用计算机生成面部表情。并且,随着科研学者们的不断研究,目前这项技术已应用在了生活中的很多领域。用计算机生成面部表情这一研究课题无论是在理论研究中,还是在实际应用中都具有十分重要的意义,广泛的应用领域使得它有着广阔的发展前景。
人类具有6种基本表情:高兴、悲伤、愤怒、惊讶、厌恶和恐惧。我们可以将这六种表情称为基表情,而其他的表情都是可以通过这些表情基线性表示 [1] [2] ,也就是说如果我们可以获得一个人的六个基本表情的三维模型,那么我们就可以利用它们生成这个人的其他表情。一般来说,我们将基本表情的三维人脸模型称为表情基,因此,如何快速而高效地生成不同的表情基,成为了生成面部表情的基础。本文针对人脸结构的特征,将人脸模型转化为三角网格模型,再根据给定的样例表情基生成目标表情基。如何将给定的样例表情基的面部表情迁移到目标人脸模型并同时考虑到目标人脸模型的个性化特征是其中的关键问题,具体描述如下:
1、量化模板表情的形变
量化模板表情的形变是表情迁移的基础,由于使用三角网格来表征人脸模型,因此模板表情的形变就可以转化为量化网格顶点的形变 [3] [4] [5] 。首先可以考虑用顶点的位移量来表征形变,但是考虑到模板模型和目标模型的差异,我们就需要按比例来对这个位移量进行缩放。基于以上两个主要因素的考虑,本文选择使用一组仿射变换来表征模板模型各三角网格的形变。
2、使用仿射变换的一致性约束网格形变
为了能尽可能真实的将模板模型的表情迁移到目标模型上,需要在网格形变的过程中添加约束,即仿射变换的一致性。仿射变换的一致性是指如果模型中的多个三角网格共用一个顶点,那么各三角形形变后也应使得公共顶点位于同一位置 [6] [7] 。该约束条件可以保证形变后的模型具有光滑的表面。
本文针对基于样例的生成面部表情基系统进行研究,研究内容主要包括将源三角网格的形变表征为仿射变换、通过仿射变换的一致性约束网格形变两个主要方面。
2. 生成算法设计
2.1. 计算样例面部表情模型的形变梯度
一般情况下,可以选择通过将面部模型转化为三角网格模型来对模型的形变进行量化分析,这也就意味着可以通过分析每一个三角网格的形变来最终确定整个模型的形变。表征形变最常用的方式就是通过位移场将每一个顶点的位移记录下来,但是这种表征方法通常只适用于较小的形变,尤其是没有形状上的变化的情况,因为这种方法只考虑了顶点在笛卡尔坐标系内的位移,而忽略了向量的变化。所以如果要用在生成面部表情上,还需要使用比位移场更加精确全面的方法来表征三角网格的形变,即不仅仅要考虑位置上的平移,还要考虑长度上的伸缩变换。因此本文选择使用仿射变换来表征三角网格的形变。
将模型分为由三个三角网格组成而成的四面体的确可以达到简化计算模型形变梯度的目的,但是同时还要考虑三角网格之间的关系。因此本文使用另一种方法生成更加独立的四面体,即为每一个三角网格增加一个垂直于三角网格方向的顶点
。
为了将新顶点放置在垂直与三角网格的方向上,并确保垂直空间与三角网格一起旋转,以及它的位置能够根据三角网格边向量长度的变化而以相同的比例进行缩放,因此定义如下公式用于计算新添加的顶点
:
(1)
其中
为L2范式。
在添加了辅助顶点
之后,就可以通过应用等式来以闭合的形式计算每个三角网格的形变梯度。也就是说,得到的形变梯度的张量场近似等于三角网格模型的表面,而不再需要对其内部进行剖析,考虑各三角网格之间存在的内部关系。
2.2. 计算目标面部表情模型的形变梯度
给目标模型的每一个三角网格都添加一个类似的辅助顶点
自然是没问题的,但实际上是没有必要的,因为这只会增加之后的计算过程的复杂度。在生成目标面部表情时,和处理给定的样例面部表情不同,它并没有真实的形变传输的过程,而是通过一系列计算得到的相应数据。所以需要关心的只有实际发生变化的目标三角网格本身的变化,而不用考虑垂直空间上的变化。因此,我们能够不需要额外添加新的辅助顶点
,得出目标模型中每个三角网格的形变梯度的表达式。
假设对于三角网格i,它的三个顶点分别为
,则
(2)
其中
和
都是3 × 2矩阵,分别包含了三角网格形变前和形变后的边向量,即:
(3)
由于矩阵
是3×3矩阵,共有9个未知量,而矩阵
和
都是3 × 2矩阵,只能提供6个等式,因此若要求解等式3-6中矩阵
,则需要对矩阵
和
进行QR因式分解,即
(4)
其中
是一个3 × 3的正交矩阵,而
是一个2 × 2的上三角矩阵,由此可以计算出,目标模型的形变梯度
:
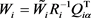 (5)
(5)
2.3. 三角网格间的映射
网格形变传递的目标是将模板模型展现的三角网格形变转移到目标模型的网格上。从概念上讲,理想的结果是非常明确的:目标模型眼睛部位的形变应该和模板模型的眼睛部位的形变相似,目标模型嘴巴部位的形变和模板模型的嘴巴部位的形变相似等等。然而,对于三角网格来说,顶点索引等数字信息里并没有表示眼睛,嘴巴等概念。即使可以借助一些工具让如眼睛,嘴巴等这样的语义信息可用,但更加精细的细节关系,如具体到每个三角形之间的对应关系,依旧是不明确的。因此,在该系统的设计过程中,需要考虑如何用一些方法来表示模板模型的三角形与目标模型的三角形之间的对应关系。
先考虑最简单的情况,如果模板模型和目标模型的网络拓扑结构相同,则模板模型的三角形与目标模型的三角形之间的对应关系应为一对一的对应关系,也就是所,目标模型的三角网格i发生的形变应该和模板模型的三角网格i发生的形变相同。
但是很多时候,让模板模型和目标模型可能拥有不同数量的顶点、不同数量的三角网格,不一样的网格拓扑结构。为了应对这些更为复杂的情况,我们需要一个映射M来表示模板模型的三角网格和目标模型的三角网格之间的映射关系。这个映射M由三角网格索引的离散对组成:
(6)
一对
表示索引为
的目标模型的三角网格应该像索引为
的模板模型的三角网格那样变形。由于对映射M没有更多的限制条件,因此该映射具有极强的通用性。在大多数情况下,M是一个多对多映射,但它也可以是双射或者满射,因此,目标模型的一个三角网格可以与模板模型的几个三角网格相匹配,反之亦然。
采用三角网格的形变梯度来表征网格变形,采用离散的三角网格配对来标识三角网格的对应关系,这是我们开始传输网格形变的两个必要条件。本文采用的策略是首先从模板模型中计算出每个三角网格的形变梯度,之后通过映射M中的对应关系,直接构建出一个形变后的目标模型。为了推导这个过程,首先考虑模板模型和目标模型具有相同的网格拓扑的情况。因此,模板模型的三角网格与目标模型的三角网格之间存在一一对应的关系,这消除了在映射M中显式的给出三角网格间关联的需要。这样设计构造好的算法,在面对更复杂的情况时,即在不同的网络拓扑间进行形变传输,也仅需要稍微更改即可。
2.4. 仿射变换的一致性
模板模型的仿射变换
的非平移部分S表征了模板模型的三角网格形状的变化。然而,它并不能直接应用于相应的目标模型的三角网格,因为S仅包含方向和大小的变化,不含有关于三角网格相与其相邻网格之间的位置信息。所以为了确保仿射变换在应用到目标模型的三角网格上时可以保持相互之间的一致性,即共享顶点的三角网格在变形后,该共享顶点依旧位于同一位置。因此对于仿射变换集合,需要定义如下约束:
(7)
其中
是共享顶点
的三角网格的集合。
为了在将模板形变传输到目标网格上并同时保持这些一致性要求,需要最小化模板模型与目标模型非平移变换的部分之间的差异,并且通过以下约束公式来确保仿射变换的一致性,其中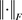 表示矩阵的范数,也可以称为佛罗贝尼乌斯范数,或者矩阵元素平方和的平方根:
表示矩阵的范数,也可以称为佛罗贝尼乌斯范数,或者矩阵元素平方和的平方根:
(8)
虽然公式(8)中的形变约束公式可以用二次规划方法解决,但与之相比更有效的方法是通过计算顶点位置来重新构造需要解决的问题,以此来消除约束条件。其中关键的思想是根据三角网格的顶点定义未知的目标网格变换。然后,我们不直接求解仿射变换的解,而是直接求变形后的顶点位置。该方法满足所有约束条件,因为通过这样的建造,任何共享顶点都将被转换到相同的位置。
2.5. 确定并优化顶点集合
为了能够尽可能准确地生成变形后的目标模型,要求必须同时求解全部顶点,而不是一次求解一个顶点。因此该系统需要一个框架来执行此计算,以防止精度误差累积和由于整个网格中变形梯度的不一致而导致的分布误差。由于模板模型中的形变梯度与目标模型的形变梯度不一致,因此不存在形变梯度与模板模型中的形变梯度完美匹配的变形目标模型。若假设S为理想中的形变梯度的集合,T为实际的形变梯度的集合,那么优化过程就可以表示为找到变形梯度T的集合并使它尽可能地接近于S中的理想变量。该过程可以通过最小化S和T中指定的矩阵之间的差异来表示:
(9)
Subject to
在目标函数中,当
等于
时,这个范数的值为零。因此,使对于所有i来说的
都为最小值就可以找到形变梯度尽可能接近理想值的网格模型。正如前面所讨论的,因为形变梯度对于平移来说是不变的,所以对于这种优化函数有无限多种解决方案:一个最优解的所有平移也是最优的。因此需要一个约束,即固定一个顶点的位置,使得解决方案是唯一的。
在模板模型和目标模型具有不同网格拓扑的一般情况下,使用网格映射集合M来规定模板模型和目标模型的哪些三角网格应该类似地变形。网格映射集合M保证了在三角网格数不同的情况下,将模板模型中的变形梯度与目标模型中的变形梯度正确的关联起来:
(10)
Subject to
该公式允许在不同拓扑结构的网格之间进行形变传输,因为网格映射集合M可以编码正确的三角网格关联。如果一个目标模型的三角网格对应于几个模板模型的三角网格,则最小化的误差将包括目标模型三角网格的形变梯度与所有相应的模板模型三角网格的形变梯度之间差的范数的总和。在考虑到所有的对应关系之后,该公式的结果始终是整体最佳的顶点集合。
3. 系统实现
本文中所涉及的系统最终在Unity3D上实现。Unity3D是由Unity Technologies开发的一个让玩家轻松创建诸如三维视频游戏、建筑可视化、实时三维动画等类型互动内容的多平台的综合型游戏开发工具,是一个全面整合的专业游戏引擎。所使用的编程语言为C#和JavaScript。
3.1. 输入模块的实现
对于系统的输入模块,首先通过从文本框里得到的用户手动输入的文件名称,确定需要读取的目标文件。之后再对这些目标文件的内容进行分析处理。为了保存OBJ文件的内容,系统创建了的一个特殊的类ObjMesh。首先分析OBJ文件的内容,按照相应的规则将顶点信息、顶点法线信息、贴图点坐标信息以及面信息都分别存储在一个链表中,然后将面信息中关于顶点索引部分的信息提取到面数组中以供之后的调用,不同于面信息的处理,对于顶点等信息,需要先对其进行去重处理,再保存进各自的数组中以供之后的调用。对于要生成的形变后的目标模型而言,首先要对它的各种数组等进行初始化,考虑到要生成的形变后的目标模型与形变前的目标模型具有相同的顶点数和三角网格数,因此直接读取形变前的目标模型的相关信息,对要生成的形变后的目标模型的各种数组等进行初始化,之后再将计算得到的顶点坐标和顶点法线等信息重新读入数组。
3.2. 输出模块的实现
对于系统的输出模块,首先通过从文本框里得到的用户手动输入的文件名称,确定新生成的形变后的目标模型要保存的文件名称。之后再对这些目标模型的内容进行分析处理并写入相应的OBJ文件。通过MeshToString函数,将Mesh中的信息按照OBJ文件的相应格式进行改写,最终生成一个包含全部网格信息并符合OBJ文件格式的字符串。最后在检测到用户点击了保存按钮之后,将生成的字符串写入到用户指定的文件中。
3.3. 图形界面
对于系统图形界面是设计部分,Unity3D平台可以直接调用GUI控件完成交互页面的设计,另外还需要考虑镜头和光源的位置,尽可能使得生成的模型清晰可辨,最终的界面展示如图1、图2所示:
4. 结论
本文使用的方法在处理模板模型与目标模型的网格拓扑相同的情况时可以做到完全由计算机自动生成且真实感良好。但是当网格拓扑不一致时则仍然需要对特征点进行手工标记,耗时较久且标记的结果会直接影响最终的目标表情基的生成质量。因此在未来的工作中,可以考虑修改三角网格间对应关系的生成方法,避免大量的手工标记,并且进一步增强生成表情基的真实感。
致谢
感谢我的导师张成文教授对于我学业和研究的指导与帮助。感谢北邮学五1116寝室全体同学的团结与友谊。感谢北邮研究生3年的教育与培养。感谢所有对我学业及论文提出意见与建议的老师和专家们。
参考文献