二次数值半径相关问题研究

Research on the Related Problems of Quadratic Numerical Radius

摘要: 本文利用Spectraloid算子及分块算子矩阵的方法研究了有界分块算子矩阵的二次数值半径不等式的问题，得到两个乘积算子的二次数值半径不等式及分块算子矩阵的二次数值半径幂不等式的性质。

Abstract: In this paper, the quadratic numerical radius of 2 × 2 block operator matrices is studied by method of Spectraloid operator and block operator matrices, and the multiplicative properties of quadratic numerical radius and power inequality of quadratic numerical radius are obtained.

1. 引言

Hilbert空间中线性算子数值域是二次型和Rayleigh商逻辑上的推广，它具有深厚的理论基础和广泛的应用价值。Hilbert空间中有界线性算子 $A$ 的数值域定义为

$W\left(A\right)=\left\{\frac{\left(Ax,x\right)}{\left(x,x\right)}：\left(x,x\right)\ne 0\right\},$

称 $w\left(T\right)=\sup \left\{\left|\lambda \right|:\lambda \in W\left(T\right)\right\}$ 为数值半径。数值域是复平面上的凸集，而且在泛函分析、动力系统稳定性分析、控制论以及量子运算领域具有重要应用。比如，根据有界线性算子数值域的定义，容易证明数值域闭包含谱集 [1] ，即

${\sigma }_p\left(A\right){{\displaystyle \cup }}^{\text{}}{\sigma }_r\left(A\right)\subset W\left(A\right),\sigma \left(A\right)\subset \overline{W\left(A\right)}.$

这个性质称为数值域的谱包含性。数值域的凸性是个极其重要的性质，也就是说如果找到数值域的一个支撑线，则意味着找到了线性算子谱分布的半平面。然而，由于凸集的连通性，数值域有时不能更精确刻画谱的分布状态，比如谱集是若干不相交子集的并集时。鉴于此，瑞典的Tretter [2] [3] 等学者在研究 $2\times 2$ 分块算子矩阵时最先引进了二次数值域的概念。

定义1.1：Hilbert空间 $X\times X$ 中的有界 $2\times 2$ 分块算子矩阵 $T=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]$ 的二次数值域定义为

$W^2\left(T\right)=\left\{\lambda \in C:\exists f,g\ne 0使得\left|\begin{array}{cc}\frac{\left(Af,f\right)}{{\Vert f\Vert }^2}-\lambda & \frac{\left(Bg,f\right)}{\Vert f\Vert \Vert g\Vert }\\ \frac{\left(Cf,g\right)}{\Vert f\Vert \Vert g\Vert }& \frac{\left(Dg,g\right)}{{\Vert g\Vert }^2}-\lambda \end{array}\right|=0\right\}$ 。

二次数值域也是复平面子集，而且应用二次数值域可以建立自伴 $2\times 2$ 分块算子矩阵的变分原理，估计算子的特征值。值得注意的是，对于有界线性算子来说，二次数值域是数值域的子集，但不一定连通，并且二次数值域也具有谱包含性质。因此，关于线性算子的谱刻画方面，二次数值域能提供比数值域更精确的信息。于是，二次数值域是一个非常热门的研究课题，受到了国内外学者的广泛关注(见 [4] [5] [6] [7] [8] )，其中需要提及的一个研究课题是二次数值半径。

定义1.2：设 $T=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]$ 是Hilbert空间 $X\times X$ 中的有界 $2\times 2$ 分块算子矩阵，其二次数值半径 $w^2\left(T\right)$ 定义为

$w^2\left(T\right)=\sup \left\{\left|\lambda \right|:\lambda \in W^2\left(T\right)\right\}$ 。

二次数值半径是刻画二次数值域的重要工具。数值半径、二次数值半径、谱半径 $r\left(T\right)$ (即， $r\left(T\right)=\max \left\{\left|\lambda \right|:\lambda \in \sigma \left(T\right)\right\}$ )和算子范数 $\Vert T\Vert$ (即， $\Vert T\Vert ={\sup }_{\Vert x\Vert =1}\Vert Tx\Vert$ )之间满足关系式

$r\left(T\right)\le w^2\left(T\right)\le w\left(T\right)\le \Vert T\Vert$ 。

据我们所知，关于经典的数值半径，有不等式

$w\left(TS\right)\le 4w\left(T\right)w\left(S\right)$ 。

如果 $T,S$ 可交换，则上述不等式变为

$w\left(TS\right)\le 2w\left(T\right)w\left(S\right)$ 。

如果 $T,S$ 可交换且是非负，则

$w\left(TS\right)\le w\left(T\right)w\left(S\right)$ 。

自然会想到的一个问题，关于二次数值半径，上述不等式是否成立呢？另外，关于经典数值半径的幂不等式

$w\left(T^n\right)\le {\left[w\left(T\right)\right]}^n,n=1,2,3,\cdots$

也是非常重要的研究课题。于是，本文将要研究乘积算子二次数值半径不等式和幂不等式等性质。

2. 预备知识

对于一般的有界线性算子数值半径具有以下结论成立。

引理2.1 [1] [4] 设 $T,S$ 是Hilbert空间 $X$ 中的有界线性算子，则

$w\left(TS\right)\le 4w\left(T\right)w\left(S\right)$ ；

如果 $T,S$ 可交换(即 $TS=ST$ )，则

$w\left(TS\right)\le 2w\left(T\right)w\left(S\right)$ 。

引理2.2 [1] [4] 设 $T,S$ 是Hilbert空间 $X$ 中的有界线性算子，如果 $T,S$ 可交换且是非负算子，则有不等式

$w\left(TS\right)\le w\left(T\right)w\left(S\right)$ 。

引理2.3 [1] [4] 设 $T$ 是Hibert空间 $X$ 中的有界线性算子，则对任意正整数 $n$ 有

$w\left(T^n\right)\le {\left[w\left(T\right)\right]}^n$

成立。

下面给出Normaloid算子、Spectraloid算子、Convexoid算子的定义。

定义2.1：对于一个有界线性算子而言，如果满足 $r\left(T\right)=\Vert T\Vert$ ，则称 $T$ 是Normaloid算子。其中 $r\left(T\right)$ 表示算子 $T$ 的谱半径， $\Vert T\Vert$ 表示算子范数。

定义2.2：对于一个有界线性算子 $T$ 而言，如果满足 $r\left(T\right)=w\left(T\right)$ ，则称 $T$ 是Spectraloid算子。

定义2.3：对于一个有界线性算子 $T$ 而言，如果满足 $\overline{W\left(T\right)}=Conv\left(\sigma \left(T\right)\right)$ ，则称 是Convexoid算子。

比较Normaloid算子，Spectraloid算子以及Convexoid算子的定义容易发现，Normaloid算子一定是Spectraloid算子；Convexoid算子也是Spectraloid算子。

分块算子矩阵二次数值半径和内部元素数值半径具有以下关系。

引理2.5：设 $T$ 是Hilbert空间 $X\times X$ 中的有界 $2\times 2$ 分块算子矩阵, $T=\left[\begin{array}{cc}A& B\\ 0& D\end{array}\right]$ 或 $T=\left[\begin{array}{cc}A& 0\\ C& D\end{array}\right]$ ，则

$w^2\left(T\right)=\max \left\{w\left(A\right),w\left(D\right)\right\}$ 。

特别地，当 $T=\left[\begin{array}{cc}A& 0\\ 0& D\end{array}\right]$ 时， $w\left(T\right)=w^2\left(T\right)$ 。

证明：当 $T=\left[\begin{array}{cc}A& B\\ 0& D\end{array}\right]$ 或 $T=\left[\begin{array}{cc}A& 0\\ C& D\end{array}\right]$ 时，容易证明

$W^2\left(T\right)=W\left(A\right)\cup W\left(D\right)$ 。

于是有 $w^2\left(T\right)=\max \left\{w\left(A\right),w\left(D\right)\right\}$ 。

当 $T=\left[\begin{array}{cc}A& 0\\ 0& D\end{array}\right]$ 时， $W\left(T\right)=Conv\left(W\left(A\right)\cup W\left(D\right)\right)$ ，其中 $Conv\left(G\right)$ 表示集合 $G$ 的凸组合，从而 $w\left(T\right)=w^2\left(T\right)$ 。

3. 主要结果及其证明

当 $T,S$ 是 $2\times 2$ 有界线性算子时，

$w\left(TS\right)\le 4w\left(T\right)w(S)$

自然成立，但是关于二次数值半径，不等式

$w^2\left(TS\right)\le 4w^2\left(T\right)w^2(S)$

不一定成立。比如设

$T=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],S=\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]$ ，

则 $w^2\left(TS\right)=1$ ， $w^2\left(T\right)=0$ ， $w^2\left(S\right)=0$ ， $w^2\left(TS\right)\le 4w^2\left(T\right)w^2\left(S\right)$ 不成立。下面我们将给出上述不等式成立的充分条件。

定理3.1：设 $T,S$ 是Hilbert空间 $X\times X$ 中的 $2\times 2$ 有界线性算子，如果 $T,S$ 是Spectraloid算子，则

$w^2\left(TS\right)\le 4w^2\left(T\right)w^2\left(S\right)$ 。

证明：当 $T,S$ 是Hilbert空间 $X\times X$ 中的有界线性算子时，由引理2.1知

$w\left(TS\right)\le 4w\left(T\right)w\left(S\right),$

且

$r\left(T\right)\le w^2\left(T\right)\le w\left(T\right)\le \Vert T\Vert ,r\left(S\right)\le w^2\left(S\right)\le w\left(S\right)\le \Vert S\Vert .$

于是

$w^2\left(TS\right)\le 4w\left(T\right)w(S)$

当 $T,S$ 是Spectraloid算子时，满足

$r\left(T\right)=w\left(T\right),r\left(S\right)=w(S)$

即

$w^2\left(T\right)=w\left(T\right),w^2\left(S\right)=w(S)$

故

$w^2\left(TS\right)\le 4w^2\left(T\right)w^2(S)$

推论3.1：如果 $T,S$ 是Normaloid算子或者Convexoid算子，则有 $w^2\left(TS\right)\le 4w^2\left(T\right)w^2\left(S\right).$

其次，我们将要讨论不等式 $w^2\left(TS\right)\le 2w^2\left(T\right)w^2\left(S\right)$ 何时成立的问题。

定理3.2：设 $T,S$ 是Hilbert空间 $X\times X$ 中的 $2\times 2$ 有界Spectraloid算子，且 $T,S$ 可交换，则有 $w^2\left(TS\right)\le 2w^2\left(T\right)w^2\left(S\right)$ 。

证明：因为 $T,S$ 是Spectraloid算子，故

$w^2\left(T\right)=w\left(T\right),w^2\left(S\right)=w\left(S\right)$ 。

再考虑到 $T,S$ 的可交换性，由引理2.1可知

$w^2\left(TS\right)\le 2w^2\left(T\right)w^2\left(S\right)$ 。

于是，结论立即得证。

推论3.2：如果 $T,S$ 是Normaloid算子或者Convexoid算子，且 $T,S$ 可交换，则

$w^2\left(TS\right)\le 2w^2\left(T\right)w^2\left(S\right)$ 。

再其次，我们将要讨论不等式 $w^2\left(TS\right)\le w^2\left(T\right)w^2\left(S\right)$ 何时成立的问题。

定理3.3：设 $T,S$ 是Hilbert空间 $X\times X$ 中的 $2\times 2$ 有界线性算子，且 $T,S$ 可交换， $T$ 是非负算子，当 $T,S$ 是Spectraloid算子时，有

$w^2\left(TS\right)\le w^2\left(T\right)w^2\left(S\right)$ 。

证明：当 $T,S$ 可交换， $T$ 是非负算子时，有

$w\left(TS\right)\le w\left(T\right)w\left(S\right)$ ，

故

$w^2\left(TS\right)\le w\left(T\right)w\left(S\right)$ 。

当 $T,S$ 是Spectraloid算子时，有

，。

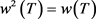于是

。

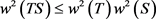结论证毕。

推论3.3：如果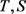是Normaloid算子或者Convexoid算子，且可交换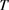，是非负算子，则

。

最后，我们将要讨论二次数值半径的幂不等式问题。

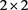定理3.4：设是分块算子矩阵的二次数值半径，则对任意正整数，有

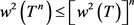
成立。

证明：因为，故

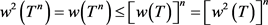
所以

。

结论得证。

定理3.5：设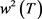是分块算子矩阵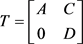的二次数值半径，则对任意正整数，有

成立。

证明：因为，从而

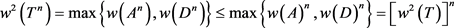
所以

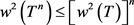
结论证毕。

同理可证下面推论：

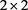推论3.4：设是分块算子矩阵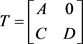的二次数值半径，则对任意正整数有

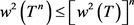
成立。

基金项目

内蒙古大学校级大学生创新创业训练计划资助项目(项目编号：201811209)，Project 201811209 supported by Inner Mongolia University Training Program of Innovation and Entrepreneurship for Undergraduates，国家自然科学基金(批准号：11561048)。

NOTES

^*通讯作者。