预应力矮肋T梁桥跨中横隔梁力学性能及计算方法分析

Analysis of Mechanical Properties and Calculation Method of Mid-Span Transverse Beam of Prestressed Low-Ribbed T-Beam Bridge

摘要: 由于预应力矮肋T梁桥结构高度小，主梁抗扭刚度小，桥梁在受力时，力在桥梁上的横向分布会与普通T梁不同，横隔梁的力学性能也会发生变化。为了解预应力矮肋T梁桥跨中横隔梁的力学性能以及掌握预应力矮肋T梁桥跨中横隔梁的合理计算方法，本文通过全桥有限元分析方法、偏心压力法理论对预应力混凝土矮肋T梁桥跨中横隔梁进行受力性能分析，然后与现场试验结果进行对比分析。结果表明：横隔梁截面应力沿梁高成线性分布；有限元分析方法的计算结果与试验结果的最大误差为9.4%，最小误差为1.5%；运用偏心压力法的计算结果与试验结果的最大误差为27.7%，最小误差为10.5%；采用偏心压力法计算的中性轴位置与实际中性轴位置有偏差。可见横隔梁受力均匀，工作状态良好；全桥有限元分析方法可很好的模拟预应力矮肋T梁桥横隔梁的受力性能，理论计算的横隔梁的应力与试验结果吻合，误差小于9.4%，计算精度高，可用于实际工程设计当中；采用偏心压力法理论对预应力矮肋T梁桥的横隔梁进行内力计算是不太适用的，计算精度不高，不能真实的反应梁的实际受力情况；偏心压力法理论计算不够精确的原因是受压翼缘板的有效翼缘宽度计算不够合理。

Abstract: Due to the small structural height of the prestressed low-ribbed t-beam bridge and the small torsional stiffness of the main beam, the transverse distribution of the force on the bridge will be different from that of the ordinary t-beam when the bridge is under stress, and the mechanical properties of the transverse beam will also change. In order to understand the mechanical properties of the mid-span transverse beam of the prestressed low-ribbed T beam bridge and master the reasonable calculation method of the mid-span transverse beam of the prestressed low-ribbed T beam bridge, based on the finite element method of the whole bridge and the theory of eccentric pressure, this paper analyzes the mechanical behavior of the mid-span transverse beam of the prestressed concrete low-ribbed t-beam bridge, and then makes a comparative analysis with the field test results. The results show that the cross section stress is linearly distributed along with the beam height. The maximum error of the finite element method is 9.4% and the minimum error is 1.5%. The maximum error of the eccentric pressure method is 27.7% and the minimum error is 10.5%. The neutral axis position calculated by eccentric pressure method deviates from the actual neutral axis position. It is concluded that the transverse beam is in good working condition. The finite element analysis method of the whole bridge can well simulate the mechanical behavior of the transverse beam of prestressed low-ribbed t-beam bridge. It is not suitable to calculate the internal force of the transverse beam of the prestressed t-beam bridge by using the theory of eccentric pressure. The theoretical calculation of eccentric pressure method is not accurate enough, and the reason is that the effective flange width calculation of the compression flange plate is not reasonable enough.

1. 引言

预应力混凝土矮肋T梁具有施工方便、受力合理、耐久性好、美观等优点 [1] [2] [3] [4] [5] 。目前我国工程界在不同类型桥梁的横隔梁力学性能及计算方面作了很多理论探讨 [6] ，并取得了很多成果。但对于这种矮肋T梁结构的横隔梁力学性能及计算方法，还缺少深入的探究。本文运用理论计算与科学试验相结合的方法，对预应力矮肋T梁桥跨中横隔梁的力学性能及合理的计算方法进行探讨。希望能为相似桥型的工程设计提供些许参考。

2. 试验研究

本文以克山4 × 16 m的简支预应力混凝土矮T梁桥为试验对象，该桥横断面由5片矮肋T梁组成，计算跨径为14.96 m，梁端及跨中设置横隔梁，横梁宽0.3 m，混凝土材料均为C50混凝土。设计荷载等级：公路I级汽车荷载。在确保计算时加载位置及加载力大小与实际加载一致的情况下，对桥梁进行静载试验，采用汽车超-20车队中的55 t重车进行加载，车辆两侧车轮中心间距1.8 m。

2.1. 试验加载工况

将跨中横隔梁视为4跨弹性支撑连续梁。测试车轮荷载作用时横隔梁受力情况，分为两个工况进行加载。工况1：对横隔梁边跨跨中位置进行正弯矩加载，加载时让55 t重车后轴单侧车轮中心压在横隔梁边跨跨中位置，车头朝向桥墩，车尾朝向跨中。工况2：加载时让55 t重车后轴单侧车轮中心压在横隔梁次边跨跨中位置，车头朝向桥墩，车尾朝向跨中。如图1~图3所示。

Figure 1. Test the longitudinal loading position

图1. 试验纵向加载位置

Figure 2. Working condition 1: lateral loading position of load

图2. 工况1：荷载横向加载位置

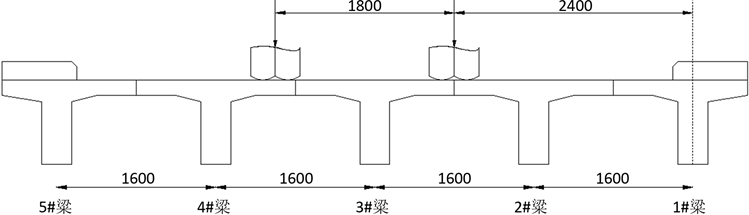
Figure 3. Working condition 2: lateral loading position of load

图3. 工况2：荷载横向加载位置

2.2. 测点布置

在车轮荷载作用下，测试横隔梁跨中受力情况时，在横隔梁边跨跨中与次边跨跨中沿竖向各预埋4个应变计，其中HY1南与HY1北表示同一竖向高度的南北两个测点，其他测点编号意义与HY1相同。如图4所示。

Figure 4. Arrangement of measuring points

图4. 测点布置

3. 理论分析方法

3.1. 全桥有限元分析

考虑到横隔梁为梁结构，建模时横隔梁采用梁单元的形式分析更加合理准确。采用Midas Civil进行桥梁的建模分析。按照实际结构情况，两端及跨中按实际尺寸设置横隔梁，其余部分采用虚拟横梁进行横向连接，横梁与主梁正交。有限元模型见图5，T梁相关参数见表1、表2，边梁和中梁钢绞线配束见表3。试验研究对应计算荷载以集中荷载形式输入，采用55 t车加载，后轴与中轴重皆为220 KN，前轴重110 KN，计算荷载在模型中的加载位置试验荷载加载位置相同。

Figure 5. Finite element model

图5. 有限元模型

Table 1. Design parameters of T beam

表1. T梁设计参数

Table 2. Geometric characteristic parameters of T beam section

表2. T梁截面几何特性参数

Table 3. T beam steel wire bundle

表3. T梁钢绞线配束

3.2. 偏心压力法

采用偏心压力法理论来计算横隔梁的内力，实际上是运用偏心压力法绘制出横隔梁的内力影响线，然后将求得的横隔梁计算荷载在相应的影响线线上进行加载，得出所求截面内力。偏心压力法适用于桥梁的宽跨比B/L小于或接近0.5的情况，基本前提是：汽车荷载作用下，中间横隔梁可近似地看作一根刚度为无穷大的刚性梁，横隔梁仅发生刚体位移；忽略主梁的抗扭刚度。本文所依托桥梁的宽跨比B/L = 0.501接近于0.5，故可按偏心压力法计算。

3.2.1. 荷载横向分布影响线

根据《桥梁工程》 [7] [8] 可知，当各主梁惯性矩相等时，荷载横向分布影响线的竖标值计算公式为：

${\eta }_{ik}=\frac{1}{n}\pm \frac{{\alpha }_i{\alpha }_k}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\alpha }_i^2}}$ (1)

${\eta }_{ik}$ ：当P = 1位于第k号主梁轴上时，对i号主梁的总作用。

${\alpha }_i$ ：各片主梁梁轴到截面形心的距离。

利用公式(1)计算出各片主梁的荷载横向分布影响线竖标值，并绘制出荷载横向分布影响线，见图6、图7。

3.2.2. 横隔梁计算荷载

对于跨中一根横隔梁的桥梁来说，加载时除了直接作用在其上的轮重外，前后的轮重对它也有影响，可以采用假设荷载在相邻横隔梁之间按杠杆原理传布的方法计算。采用55 t车加载，后轴与中轴的轴重为220 KN，前轴重110 KN，所计算的作用在横隔梁上的计算荷载为P0q = 225.5 KN。

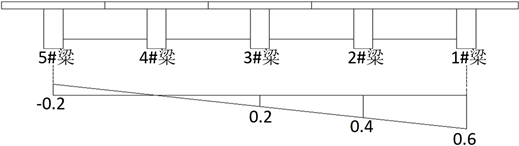
Figure 6. Influence line of transverse distribution of load on 1# beam

图6. 1#梁荷载横向分布影响线

Figure 7. Influence line of transverse distribution of load on 2#

图7. 2#梁荷载横向分布影响线

3.2.3. 横隔梁计算荷载

由《桥梁工程》(第四版)可知，横隔梁任意截面r的内力计算公式为：

荷载P = 1位于截面r的左侧时

$M_r{\displaystyle \underset{左}{\sum }{R}_i{b}_i}-e$ (2)

荷载P = 1位于截面r的左侧时

$M_r{\displaystyle \underset{左}{\sum }{R}_i{b}_i}$ (3)

${\displaystyle \underset{左}{\sum }{R}_i}$ ：所求截面以左全部支撑反力 $R_i$ 的总和，支撑反力 $R_i$ 可有2.3.1节绘制的荷载横向分布影响线求得。

$b_i$ ：支撑反力 $R_i$ 至所求截面距离。

e：荷载P = 1至所求截面距离。

由公式(2)、(3)计算出横隔梁内力影响线的竖标值，绘制出横隔梁边跨跨中与次边跨跨中截面的内力影响线，见图8、图9。

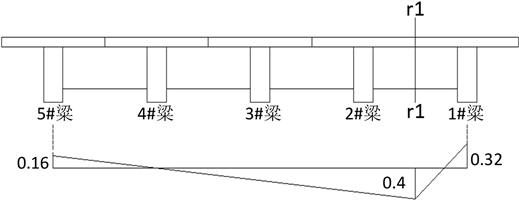
Figure 8. r1 section internal force influence line

图8. r1断面内力影响线

Figure 9. r2 section internal force influence line

图9. r2断面内力影响线

在不计入冲击系数的情况下，根据内力影响线及计算荷载的加载位置求出r1、r2截面弯矩内力值为：Mr1 = 140 KN∙m，Mr2 = 272 KN∙m。

3.2.4. 横隔梁截面应力计算

在计算横隔梁应力的时候需考虑剪力滞的影响，横隔梁受力时两侧的翼缘板协同参与受压。经过计算横隔梁上缘参与受压的翼缘板有效宽度λ = 3.0 m，则横隔梁应力计算截面图示见图10，截面应力计算公式为：

$\sigma =\frac{M\cdot y}{I}$ (4)

M：截面弯矩，Mr1 = 140 KN∙m，Mr2 = 272 KN∙m。

y：截面中性轴至所求应力点的垂直距离。

I：截面惯性矩。

Figure 10. Stress calculation cross section of transverse beam

图10. 横隔梁应力计算截面

4. 计算结果及对比分析

为了分析预应力矮肋T梁桥横隔梁的受力性能以及验证理论计算的正确性，在技术标准和加载工况相同的情况下，运用全桥有限元分析法、偏心压力法对结构进行分析，并将计算结果与试验研究所得结果进行对比分析。工况1、工况2荷载作用下横隔梁跨中各测点应力计算及试验结果对比分析见表4、表5以及图11、图12所示。

Table 4. Stress comparison in working condition 1

表4. 工况1应力比较

Figure 11. Comparative analysis of stress in working condition 1

图11. 工况1应力对比分析

Table 5. Stress comparison in working condition 2

表5. 工况2应力比较

Figure 12. Comparative analysis of stress in working condition 2

图12. 工况2应力对比分析

从表4、表5中可以看到各测点试验结果的均方差为 ${\sigma }_{\text{HY1}}=0.01$ 、 ${\sigma }_{\text{HY2}}=0.005$ 、 ${\sigma }_{\text{HY3}}=0.06$ 、 ${\sigma }_{\text{HY4}}=0.005$ 、 ${\sigma }_{\text{HY5}}=0.015$ 、 ${\sigma }_{\text{HY6}}=0.015$ ，表明数据离散程度小，试验结果具有可靠性，试验结果可用于与各计算方法的分析结果进行对比分析。运用有限元分析方法的计算结果与试验结果的最大误差为9.4%，最小误差为1.5%，运用偏心压力法的计算结果与试验结果的最大误差为27.7%，最小误差为10.5%。

由图11、图12可知，工况1、工况2试验测得应力值与计算所得应力值皆沿梁高成线性分布，而运用有限元分析方法绘制的应力沿梁高变化曲线与试验所得曲线更加吻合，且中性轴位置接近。

从图11、图12可知，采用偏心压力法计算的中性轴位置与实际位置有偏差，由2.2.4节可看到影响中性轴位置的因素是受压翼缘板的有效翼缘宽度。

5. 结论

1) 横隔梁受力时应力沿梁高成线性分布，横隔梁受力均匀，工作状态良好。

2) 全桥有限元分析方法可很好的模拟预应力矮肋T梁桥横隔梁的受力性能，理论计算的横隔梁的应力与试验结果吻合，误差小于9.4%，计算精度高，可用于实际工程设计当中。

3) 采用偏心压力法理论对预应力矮肋T梁桥的横隔梁进行内力计算是不太适用的，计算精度不高，不能真实的反应梁的实际受力情况。

4) 采用偏心压力法理论计算不够精确的原因是受压翼缘板的有效翼缘宽度计算不够合理。