1. 引言
为了解决高层建筑的结构承载问题,建筑体系和结构形式持续进步和创新。其中型钢–混凝土组合结构与传统的钢混结构和钢结构相比具有独特的性能优势,被普遍地用于世界各国高层建筑的设计中。作为重要的城市标志性建筑,型钢–混凝土组合结构一旦在地震灾害中遭受破坏,势必将产生巨大的经济损失,极大地影响到地震救灾和震后重建工作。因此,对其抗震性能的研究具有重要的现实意义。
对于由混凝土材料组成的高层结构而言,因材料碳化、冻融循环、温度效应等因素影响,材料自身力学性能在服役期内会发生较大的变化 [1],进而会影响结构的抗震能力。当前常规的结构抗震设计只针对完好结构,尚未考虑服役期内材料性能的劣化,使得面向完好结构的抗震性能设计与服役期内实际结构的真实性能存在差距,这样的差距对于设计精度较高的复杂高层建筑的影响往往是不可忽视的。
对于突发地震载荷下结构损伤的研究,大量的国内外学者致力于量化损伤状态指标和建立地震损伤模型。例如,王振宇 [2] 和沈祖炎 [3] 等基于各类地震损伤模型,从材料、构件和结构3个层次对国内外结构地震损伤评估的研究成果进行了系统总结和综合评述。在结构层面,主要是利用整体法和加权组合法来计算结构的地震损伤。比如:Messina等 [4] 通过遭遇地震作用前后,部分构件基本频率的变化情况来评估结构损伤,在此基础上顾祥林 [5] 建议以结构频率作为损伤指标来定义整体结构的损伤状况。而Ang H.S等 [6] 以构件的能量消耗率作为权重系数,将构件损伤值进行加权组合得到楼层损伤值,继而对楼层损伤进行加权组合得到整体结构的损伤。
在抗震设防的领域,结构易损性的定义是:对于地面运动的给定参数值,构件发生超过某个损伤程度的条件概率 [7]。目前,结构易损性理论在工程实际中已有较为成熟的实践和应用,各国学者对易损性理论的研究也取得大量成果,先后形成了多种分析方法,主要包括经验易损性分析方法和理论易损性分析方法 [8],后者由于适用范围广、限制条件少的特点,得到了广泛的应用和发展。2000年,Karim和Yamazaki [9] 率先提出利用数值模拟方法来建立易损性曲线。Shinozuka [10] 采用Monte Carlo模拟法得到了桥梁的地震易损性曲线。庞于涛等 [11] 结合人工神经网络方法(ANN)建立结构随机能力模型,并通过增量动力分析(IDA)获得结构响应,形成地震易损性曲线。H. Hwang和刘晶波 [12] 基于地面运动、局部工程场地条件和桥梁本身参数三个方面的不确定性,提出一种直接回归概率需求模型线性拟合法来评估结构的地震易损性,并对美国中东部受New Madrid地震带影响的高速公路系统的易损性进行分析。何益斌等 [13] 分别以结构最大层间位移角和最大顶点位移角作为结构整体性能指标,结合性能水平限值来有效地评估结构的地震易损性。
众多研究均未考虑组合结构由于材料的性能劣化所引起的损伤以及抗震性能衰减的时变效应。本文即以复杂高层型钢–混凝土组合结构为研究对象,考虑材料在服役期内的性能劣化,基于增量动力分析(IDA)获得了结构在不同服役年限时遭遇地震的响应,并根据地震损伤模型和理论地震易损性分析方法,绘制结构地震易损性曲线,研究结构的材料时变特性对结构损伤和抗震性能的影响,评估结构在服役期内的抗震性能。
2. 复杂高层型钢–混凝土组合结构时变地震易损性分析
本文面向型钢–混凝土组合结构,考虑混凝土在服役期内的劣化过程,提出一种考虑材料时变特性的地震易损性分析方法,其技术路线如图1所示。首先,选取合理的混凝土材料时变模型,通过改变弹性模量、抗压强度等材料参数来反映材料的时变特性。然后利用商业有限元软件建立考虑材料时变特性的复杂高层型钢–混凝土结构模型,并利用增量动力分析(IDA)得到在不同服役期内遭遇突发地震灾害的结构动响应。接着,选取合理的性能指标和损伤判别准则,建立具备损伤等级对照标准的结构地震损伤模型。最后,结合地震损伤模型和结构地震响应,基于传统可靠度理论形成易损性曲线,探讨复杂高层型钢–混凝土组合结构在各服役期内的失效模式和损伤概率,为评估此类结构的抗震性能和预测预防结构地震灾害提供理论依据。
2.1. 混凝土材料时变模型
混凝土材料的劣化机理复杂,国内外科研工作者基于现场统计大数据的现场实测法和实验室模拟环境法等,获取了大量混凝土强度的实测数据和试验数据,分析了不同气候和不同环境下强度的时变规律,建立了一系列强度均值时变效应的理论模型 [14]。高向玲、李杰等 [1] 结合国外多因素综合分析概念,通过回弹法和钻孔法,检测了大量服役期为1~60年的建筑,收集大量的统计数据,并通过假设检验和参数估计方法得到混凝土强度时变概率分布函数,建立了一个新的混凝土材料强度时变模型。该模型能直观地反映混凝土强度时变效应对于结构承载能力的影响,且适用年限期限较长,故本文选用此模型进行分析。
该混凝土强度时变模型可描述为:
(1)

Figure 1. Technical route for seismic vulnerability analysis considering time-varying properties of materials
图1. 考虑材料时变特性的地震易损性分析的技术路线
式中,
为服役t年时的混凝土强度,
为混凝土标准抗压强度。
根据上述模型以及材料的弹性模量与其抗压强度之间的关系式,建立混凝土材料的弹性模量时变模型:
(2)
2.2. 地震损伤模型
地震易损性分析的前提条件是定义一个合理的结构损伤的界定标准。层间位移角既是高层建筑结构地震变形的重要控制参数,也是基于首次被超越准则的建筑结构地震损伤模型的重要性能指标。很多的学者基于层间位移角对高层建筑的损伤状态进行评估,并提出了与上述定性的损伤描述所对应的定量的损伤值范围。参照多位研究者的结论 [14] [15],本文提出以层间位移角作为设计参数的地震损伤评估模型,如式(3)所示。
(3)
其中,
为服役期某时刻结构的层间位移值;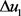 、
、
和
、
、
和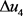 分别对应结构达到轻微损伤、中等损伤、严重损伤和倒塌状态时的层间位移限值。此模型的损伤值D的取值范围为[0,1),无论层间位移如何变化结构损伤值只能接近而无法达到1,当损伤值D达到0.8时表示结构已经达到倒塌极限状态。此模型能够与结构损伤等级和地震设防水准直接联系,能直观评价结构的抗震性能是否达到相应的设防标准。
分别对应结构达到轻微损伤、中等损伤、严重损伤和倒塌状态时的层间位移限值。此模型的损伤值D的取值范围为[0,1),无论层间位移如何变化结构损伤值只能接近而无法达到1,当损伤值D达到0.8时表示结构已经达到倒塌极限状态。此模型能够与结构损伤等级和地震设防水准直接联系,能直观评价结构的抗震性能是否达到相应的设防标准。
各个性能水平对应的层间位移限值是层间位移角限值和楼层层高的乘积,即:
(4)
式中,
为层间位移角限值,h为计算层层高。根据抗震设防的三水准要求:结构保持基本完好符合小震不坏的设防要求、结构发生轻微损伤和中等损伤满足中震可修的设防要求、结构发生严重破坏满足大震不倒的设防要求。根据《建筑抗震设计规范》,本文界定地震破坏的不同等级的4个层间位移角限值分别为1/800、1/400、1/200和1/100。表1显示了地震损伤对应的5个等级,层间位移角的限值和该模型定义的损伤值三者的对应关系。

Table 1. Classification of seismic performance level of complex high-rise steel-concrete composite structures [15]
表1. 复杂高层型钢–混凝土组合结构抗震性能水准的划分 [15]
2.3. 结构地震易损性分析
目前,国内外学者研究地震易损性的主流方法分为两种:经验易损性方法和理论易损性方法 [8]。其中,后者又分为基于数值模拟的损伤超越统计法和基于可靠度的直接回归拟合法 [8]。第二种方法基于确定性有限元分析获得大量的地震响应,作为统计分析的样本,进行易损性分析并绘制易损性曲线。这个方法的基本假设是在不同地面运动强度下,结构的响应可通过对数正态分布进行拟合,并假定结构损伤概率服从对数正态分布。
在地震易损性分析中,获取结构的地震响应的方法主要是增量动力分析(IDA)。该方法将单一的时程分析扩展为增量时程分析,综合了静力推覆分析和非线性时程分析的诸多优点,在抗震分析中有着大量应用。
本文基于可靠度的直接回归拟合法,通过增量动力分析得到结构的地震响应,结合结构地震损伤模型,计算地震损伤值,将地震损伤值对数化后进行线性回归拟合,计算结构在不同损伤状态下的超越概率,最终绘制易损性曲线。本文绘制地震易损性曲线具体的过程如下:
1) 按照地震波的选取原则,选择足够数量的地震波,并对地震波进行预处理,即控制地震持续时间、截取代表性波段以及进行调幅处理。
2) 选取合理的抗震性能指标,定义合理的结构损伤破坏状态以及相应的损伤极限值,建立地震损伤模型。
3) 结合所选的调幅地震波对型钢-混凝土组合结构的有限元模型进行一系列非线性时程分析(IDA),得到层间位移角和层间位移等地震响应。
4) 基于建立的地震损伤模型,计算与各结构响应值对应的损伤值。
5) 将地震损伤值对数化后进行线性回归分析,得到结构地震损伤对数值与地震波参数(地面加速度峰值(PGA))对数的线性回归方程,如式(5)所示。
 (5)
(5)
6) 计算结构在不同破坏阶段的超越概率,绘制地震易损性曲线。结构超越目标极限性能的失效概率为:
(6)
式中:
为结构地震损伤值;
为结构某一破坏阶段的极限状态损伤值。因为
和
均服从正态分布,所以特定的失效概率可表示为
(7)
根据文献 [12],当易损性曲线以PGA为自变量时,
取为0.5。
3. 算例分析
3.1. 工程模型的建立
基于结构有限元分析软件MIDAS GEN建立如图2所示的高层型钢–混凝土组合结构模型。模型由型钢混凝土混合柱、钢框架梁和钢筋混凝土核心筒组成,具体的构件材料和截面尺寸如表2所示。总高度为90 m,共20层,各层层高4.5 m,标准层的平面布置图如图2所示。该结构符合《建筑抗震设计规范》的要求,外部框架结构和核心筒结构的抗震等级为一级,抗震设防烈度为8度,设计使用年限为60年。

Table 2. Material and section size list of components
表2. 构件的材料和截面尺寸表

Figure 2. Standard floor plan and schematic diagram of structure
图2. 结构标准层平面图及结构示意图
采用塑性铰模型进行动力弹塑性时程分析,如图3所示,包括3D梁–柱单元和3D墙单元,前者如图3(a)所示,其节点内力和节点位移分别如式(8)和式(9)所示。
(8)
(9)
后者如图3(b)所示,单元由位于墙体中央的线单元和连接于该线单元上下两端的刚体梁单元组成的,中间的线单元与3D梁–柱单元具有相同的受力特点。上述各图所示的弹簧并非真实的弹簧结构,只表明塑性变形会集中发生在图示中的弹簧位置。
本文选取的型钢混凝土柱铰的滞回模型为克拉夫双折线模型,型钢梁铰为标准双折线模型,钢筋混凝土墙铰的为修正武田三折线模型,这三种模型分别如图4所示。
3.2. 结构增量动力分析(IDA)
进行地震易损性分析的前提是获取结构大量的地震响应作为统计分析的样本,增量动力分析(IDA)是获取大量地震响应的较好的一种方法。其基本步骤是对结构施加一个地震动记录(地震波),将这一地震动记录按一定的比例系数调整为多个强度水平的地震动,并在每一强度水平下分别进行时程分析,然后利用插值的方法得到一条工程需求参数与地震动强度指标的关系曲线,即IDA曲线。更换地震动记录,获得多条IDA曲线,对其进行统计分析,以评估在不同地震水准下的结构的抗震性能。
 (a) 3D梁–柱单元
(a) 3D梁–柱单元  (b) 墙单元
(b) 墙单元
Figure 3. Schematic diagram of plastic hinge
图3. 塑性铰示意图
本文选取的15条地震波如表3所示,选择各个地震波中较有代表性的一段,控制地震持续时间为30 s,以峰值加速度PGA作为地震动参数,将15条地震波的PGA从0.1 g调整至1.0 g,得到150条地震动记录,分别进行动力弹塑性时程分析。图5给出了在Elcent地震波(PGA = 0.1 g)的作用下,算例结构顶层的层间位移随时间变化的曲线图。统计结构在不同地震波和不同地震动强度下的最大层间位移和层间位移角,并根据地震损伤模型计算地震损伤值,绘制出该型钢-混凝土组合结构的设计IDA曲线,即不同峰值加速度所对应的地震损伤图线,如图6所示。
 (a) 克拉夫双折线模型
(a) 克拉夫双折线模型 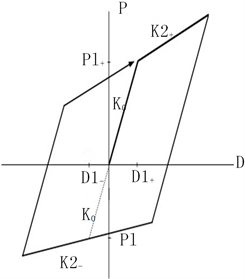 (b) 标准双折线模型
(b) 标准双折线模型  (c) 修正武田三折线模型
(c) 修正武田三折线模型
Figure 4. Hysteresis model
图4. 滞回模型
从图6中可以发现,由于地震波的频谱特性的差异,结构在不同地震波作用下的层间位移角也有明显的区别,绘制出的IDA曲线表现出一定的离散性。图6中的序号指的是表3中各个地震波序号。
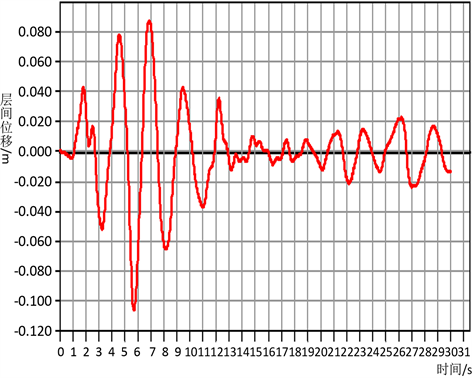
Figure 5. Top layer displacement time history diagram
图5. 顶层层间位移时程曲线图
3.3. 地震易损性分析
基于2.3节中的方法进行易损性分析,并绘制算例的设计地震易损性曲线。首先,将图6中的IDA曲线中各地震损伤值对数化后进行线性回归分析。PGA的对数值作为横坐标,地震损伤对数值为纵坐标,利用MATLAB软件进行线性回归分析,得到线性回归函数。本模型的设计地震易损性曲线的线性回归分析过程及线性回归方程如图7所示。
基于上述线性回归分析的结果,根据式(6)和式(7)计算结构在不同破坏阶段的超越概率,得到算例结构的设计地震易损性曲线,如图8所示。
从图8中可以发现,算例的设计地震易损性总体上随地震强度增大而不断提高。当PGA低于0.2 g时,结构发生轻微损伤和中等损伤的概率随地震动强度的加大而迅速增加,说明在此阶段内,该结构处于轻微和中等损伤状态且损伤发展十分迅速,结构对地震动强度的变化敏感。当PGA达到0.2 g时,结构发生轻微损伤超越概率基本达到100%,并且当地面峰值加速度达到0.5 g时,结构已经处于中等损伤状态。结构发生严重损伤情况要在PGA超过1.0 g时才可能出现,当PGA超过2.0 g时结构才有倒塌的可能,且发生两种损伤情况的超越概率随地震强度增长的速率较为平缓。当PGA小于0.6 g时,相同PGA作用下,结构倒塌的超越概率要远小于前三种损伤概率,说明该型钢-混凝土结构具有良好的安全性,不易发生倒塌。
3.4. 结构时变地震易损性分析
由于混凝土材料的性能呈现时变特性,结构在服役期间的抗震性能会随着材料性能的改变而改变。本节将2.1节中混凝土材料的性能时变模型与上述整个地震易损性分析的过程相结合,获得不同服役期遭遇地震的结构易损性曲线,以评估算例结构在整个服役期间内抗震性能的变化情况。
根据式(1)和式(2),计算出算例模型中的混凝土材料在不同年限下的抗压强度和弹性模量的时变规律,计算结果如表4所示。
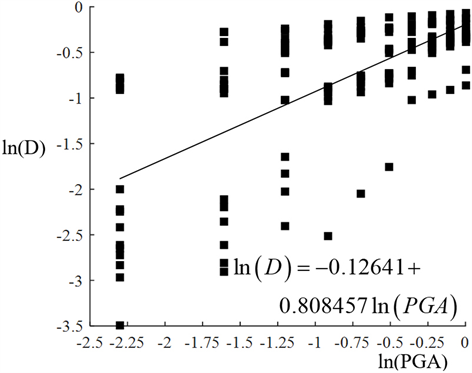
Figure 7. Linear regression analysis and equations
图7. 线性回归分析及回归方程
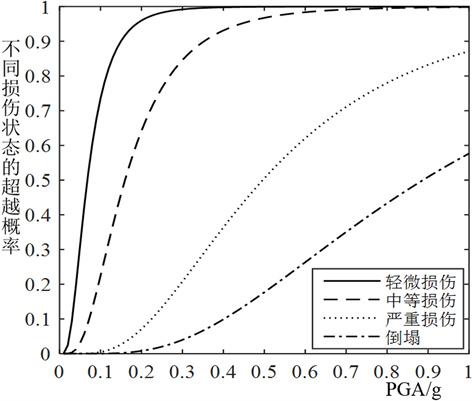
Figure 8. Design seismic vulnerability curves
图8. 设计地震易损性曲线


Table 4. Compressive strength and elastic modulus of concrete at different ages
表4. 混凝土在不同年限下的抗压强度和弹性模量
将服役期5~60年间每隔5年的时变力学性能参数输入型钢–混凝土组合结构模型,不断更换地震波的输入,采用IDA法计算结构的时变响应,根据结构的损伤模型获得时变损伤值,并逐一将其对数化后进行线性回归分析,最后得到时变地震易损性曲线,如图9~12所示。
图9为结构在不同服役时刻遭遇地震发生轻微损伤时的易损性曲线。可以看出,当PGA 达到0.2g时,结构发生轻微损伤的超越概率已接近100%。为了便于分析,该图只截取了PGA在[0,0.2]的区段。将图中设计地震易损性曲线与不同的服役时期发生地震的时变易损性曲线进行比较可以发现,结构发生轻微损伤的概率会受到材料特性的影响。当服役60年、55年以及50年遭遇地震时,结构发生轻微损伤的概率明显超过了设计概率值,这是因为弹性模量等性能指标的改变会导致结构刚度随之发生变化,从而影响到了结构的抗震性能。根据《建筑抗震设计规范》,本算例结构遭受多遇地震时,PGA取为0.07 g;而遭受罕遇地震时,PGA应取为0.4 g。从图中可以看出,在各服役时刻,结构遭遇到多遇地震时发生轻微损伤的概率在45%至55%左右。结构在服役第45~60年间发生轻微损伤的概率显著增加,这表明当结构服役45年后,随着材料弹性模量等性能指标的下降,结构刚度降低,如若遭遇到多遇地震,结构很可能开始进入塑性变形阶段。

Figure 9. Time-varying seismic vulnerability curves for minor damage
图9. 轻微损伤的时变地震易损性曲线
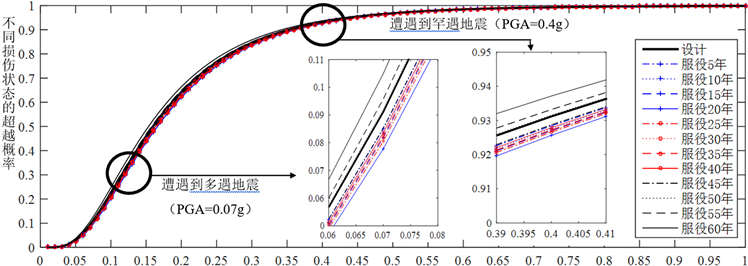
Figure 10. Time-varying seismic vulnerability curves of moderate damage
图10. 中等损伤的时变地震易损性曲线
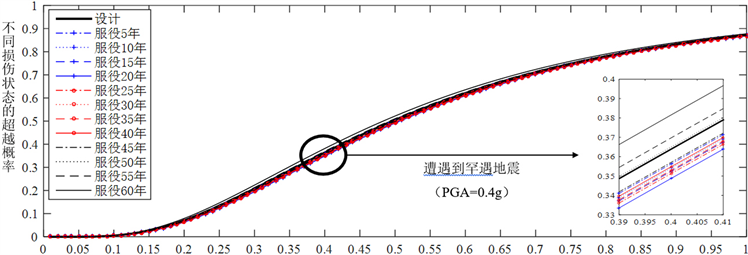
Figure 11. Time-varying seismic vulnerability curves of severe damage
图11. 严重损伤的时变地震易损性曲线
图10和图11为结构在服役期内遭遇地震发生中等损伤和严重损伤的易损性曲线。可以看出,在不同的损伤状态下,结构的地震易损性概率随着材料的时变特性而不断变化。并且在服役的前45年内超越概率的改变相对来说并不明显,这是由于本文的算例结构使用的材料时变模型显示出混凝土材料在一般的大气环境之下服役20年之后才开始逐渐劣化,即结构在服役前二十几年,并没有发生显著的材料劣化现象。从图10可以看出,在各服役时刻,结构遭遇到多遇地震发生中等损伤的概率在7%至11%左右;而遭遇罕遇地震发生中等损伤的概率在92%至94%左右。从图11可以看出,在各服役时刻,结构遭遇到多遇地震不太可能会发生严重损伤;而遭遇罕遇地震发生中等损伤的概率在34%至38%左右。当PGA为0.07 g,即当服役第60年遭遇多遇地震时,发生中等损伤的概率为0.106,设计概率为0.09,前者比后者高了约17.8%,表明材料的时变性能会影响结构的抗震性能。当PGA为0.4时,即当服役60年遭遇罕遇地震时,发生中等损伤的概率为0.936,设计概率0.929,前者比后者高了约0.75%。当PGA为0.4时,即服役第60年遭遇罕遇地震时,发生严重损伤的概率为0.382,设计概率0.362,前者比后者高了约5.5%。
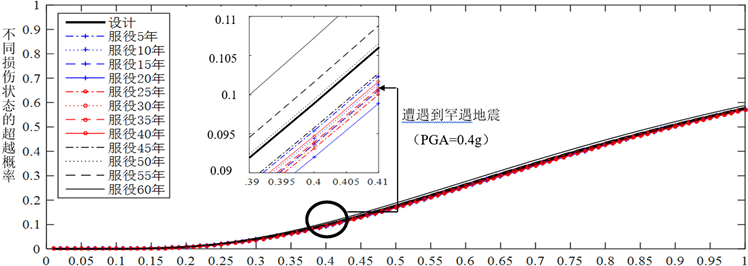
Figure 12. Collapse time-varying seismic vulnerability curves
图12. 倒塌的时变地震易损性曲线
图12为结构在服役期内遭遇地震发生倒塌的易损性曲线。从图中可以看出,在各个服役期时刻,结构遭遇罕遇地震时倒塌的概率在9%至11%左右,且在不同服役期间,结构倒塌的超越概率因混凝土材料时变特性而发生变化。当PGA为0.4 g时,当服役第60年遭遇罕遇地震时,发生倒塌的概率为0.108,设计概率0.097,前者比后者高了约11.3%;当服役第55年遭遇罕遇地震时,发生倒塌的概率为0.101,设计概率0.097,前者比后者高了约4.1%,说明材料的时变性能会影响结构的抗震性能。
4. 结论
本文研究了材料的时变特性对复杂高层型钢–混凝土组合结构抗震性能的影响,基于增量动力分析(IDA)获得了组合结构在不同服役年限遭遇地震时的动响应,依据结构性能对照标准和地震损伤模型,绘制了设计易损性曲线和时变易损性曲线,获得了如下主要结论:
1) 考虑材料的性能劣化和时变特征,可以更为准确地分析和评估不同服役期间的复杂高层型钢–混凝土组合结构的抗震性能;
2) 地震易损性曲线直观地反映了某一水平的地震动作用下组合结构的破坏概率。就本文的组合结构而言,设计地震易损性总体上随地震强度增大而不断提高。当地震动强度较小时,该结构处于轻微和中等损伤状态且损伤发展十分迅速,表明此时结构对地震动强度的变化十分敏感。结构发生严重损伤和倒塌的概率随地震强度增长的速率较为平缓,且结构倒塌的超越概率要远小于前三种损伤,说明该型钢–混凝土结构具有良好的安全性,不易发生倒塌。
3) 地震作用下组合结构的地震易损性曲线呈现出一定的时变特性,与不考虑材料时变性能的设计地震易损性曲线存在差异。在服役的前期超越概率的改变尚不明显,但在服役后期,不同损伤的超越概率已经明显超过了设计概率值,例如,在服役第60年遭遇多遇地震时,发生轻微损伤的概率比设计概率高了约7.8%。在服役第60年遭遇罕遇地震时,发生严重损伤的概率比设计概率高了约5.5%,发生倒塌的概率比设计概率高了约11.3%。这是因为材料弹性模量等性能指标的改变会导致结构刚度随之变化,从而影响了结构的抗震性能。因此,本文提出的基于材料时变特性的钢-混组合结构地震易损性分析方法能够直观地反映结构在不同服役期内抗震性能的差异,可以为结构预测预防地震灾害提供一定的依据。
基金项目
国家自然科学基金面上项目(51678135);江苏省自然科学基金面上项目(BK20171350)。