基于BP神经网络的房价预测研究——以邯郸市为例

Forecast of Housing Price Based on BP Neu-ral Network—Taking Handan as an Example

摘要: BP神经网络是截止目前应用最为广泛的一种网络结构模型，其对变量之间的非线性关系有着极强的拟合映射能力。本文以邯郸市2003年至2016年的平均房价以及主要因素数据为对象，采用BP神经网络来构建房价预测模型。实验结果显示，在相对稳定的外部环境下，BP神经网络对邯郸市的房价实现了有效预测。

Abstract: BP neural network is a network structure model, which is the most widely used currently. It has a strong ability to fit and map the nonlinear relationship between variables. This paper takes the average house price and main factor data of Handan from 2003 to 2016 as the object, and uses BP neural network to construct a house price forecasting model. The experimental result shows that BP neural network can effectively predict the housing prices in Handan in a relatively stable ex-ternal environment.

1. 引言

房价涨跌背后的原因十分复杂，其受到很多因素的影响，比如市场供需、相关政策法规的出台、房屋自身特征、地区生产总值、房地产投资、人口总量等，这使得对于房价的研究变的更加困难。由于全盘考虑相关因素对房价的影响是十分困难与不现实的，所以本文的定量研究中并没有考虑相关外部环境以及房屋自身特征等因素，如市场供需平衡、相关政策法规、房屋自身特征等因素本文都不予考虑。房价的变化趋势与影响因素之间往往呈现一种复杂的非线性关系，而传统的研究方法，如线性模型等，在处理非线性关系时误差往往比较大。而BP神经网络在处理非线性关系时具有十分突出的性能，在实际操作中，通过不断调整相关参数即可得到预测结果。目前BP神经网络的发展已经十分成熟，在理论及实操中都取得了巨大进步，已是当下应用最多的一种网络拓扑结构。本文采用BP神经网络模型来对邯郸市2003年至2016年间的房价数据进行模型训练与仿真。

2. BP神经网络的概述

2.1. BP神经网络基本原理

人工神经网络(ANN)，是通过对人脑神经系统的抽象和建模而得到的简化模型，是一种具有大量连接的并行分布式处理器，由简单的处理单元组成，具有通过学习来获取知识并解决问题的能力 [1]，尤其在处理非线性函数关系时性能十分突出。

BP神经网络是一种基于反向传播算法的多层前向网络，除了含有输入层和输出层之外，还具有一个或多个隐含层。每层的处理单元只接收来自上一层处理单元输出的信号，并将接收到的信号进行处理之后，输入至下一层，最终模型结构是一个各层处理单元之间全连接，同层处理单元之间无连接的前向无环网络拓扑结构，其网络结构如图1所示。

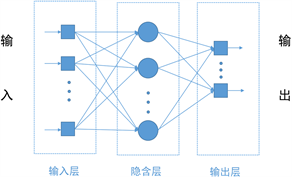
Figure 1. 3 Layer forward network architecture

图1. 3层前向网络结构

BP神经网络的学习过程由信号的正向传播与误差的反向传播构成。在输入信号的正向传播阶段，信号由输入层进入网络，经过隐含层的逐层处理之后，最终传递至输出层，得到网络的预测值。若此预测值与期望值不符，网络将转入误差的反向传播阶段。在误差的反向传播过程中，将期望值与预测值之间的误差经隐含层逐层向输入层传递，由此得到各层各单元的误差信号，然后依此误差信号实现对网络连接权值的更新。在训练过程中，反复执行信号的正向传播与误差的反向传播，直到网络输出的误差小于预先设定的阈值，或进行到预先设定的学习次数为止 [1]。

2.2. BP神经网络的学习算法

由于BP神经网络能够通过隐层神经元之间的连接自动学习输入数据的内在规律，具有强大的自学习能力而被广泛应用。BP算法的实质是从输入经过非线性映射到达输出的问题。通过梯度下降法迭代权值，以样本的输出与期望输出的偏差极小为目标进行学习，使权值误差沿误差函数的负梯度方向改变，学习的实质是不断修改权值，使得输出值与实际值尽可能地接近，直到网络各权值便不再改变，对任何符合条件的输入，网络都会给出一个相应的输出结果。

BP神经网络的算法是BP神经网络的学习过程可以分为两个阶段：

第一个阶段就是输入已知的样本值，通过网络结构和前一次迭代的权值与阈值，计算出神经元的输出。

第二阶段就是对权值和阈值进行修正，首先是从最后一层向前计算出各权值阈值对总误差的影响，然后再根据这对各权值阈值进行修改。这两个过程反复交替，直到达到我们的预期为止。

2.3. BP神经网络的应用

由于误差反向传播(Error Back Proragation, BP)网络具有：1) 非线性映射能力；2) 较强的泛化能力等很多传统计量经济方法中没有的性质。而事实上，实际应用中90%的神经网络系统都是基于BP算法的，作为人工神经网络中最为常用的算法模型，BP神经网络具有较为完备的理论基础。因此，BP神经网络在诸多领域都得到了广泛应用，主要包括：1) 航空航天业：高性能飞机自动驾驶仪、飞行器控制系统、自动驾驶增强等；2) 汽车业：汽车自动驾驶系统、保单行为分析；3) 银行业：支票和其他文档读取、信用卡申请书评估；4) 国防工业：武器制造、目标跟踪与识别、脸部认识、声呐雷达、信号/图像识别；5) 金融业：房地产评价、房价预测、贷款指导、抵押审查、信用曲线分析、货币价格预测等 [2]。

3. 基于BP神经网络的房价预测模型构建

3.1. 房价预测数据的说明

影响房价因素的选取对模型构建有着巨大影响，选取的因素应该能够客观充分反应房价的变化趋势。而影响房价变化的因素十分复杂，诸如市场供需、政策变化、房屋自身特征等因素量化起来十分困难，所以同时考虑所有相关因素对房价的影响也十分不易。基于此种考虑，本文根据实际情况以及相关文献资料选取了以下6个影响因素作为预测房价变化趋势的指标：地区生产总值/万元、建筑业总产值/万元、城镇居民人均可支配收入/元、城镇居民储蓄存款余额/万元、历年总人口/万人、城镇化率%。平均房价/元∙m⁻² = 商品房销售额/商品房销售面积。本文选取《邯郸统计年鉴》2003年至2016年间的数据作为建模数据，数据详情如表1所示。

由于在采集到的原始数据中，各变量之间的数量级存在着非常大的差异，对网络的收敛速度以及计算结果会产生不可预知的结果，因此需要对其进行归一化处理，本文采用离差标准化方法对原始数据进行线性变换，把其映射在区间[0, 1]上，映射函数为：

$x^{\ast }=\frac{x-\min \left(x\right)}{\max \left(x\right)-\min <span\; class="bracketMark">(\; x\; )</span>}$

$x^{\ast }$ 与 $x$ 分别为归一化后的值与原始值， $\min \left(x\right)$ 与 $\max \left(x\right)$ 分别为 $x$ 的最小值与最大值。在得到仿真结果之后，还需通过反归一化得到正常值，本文采用R语言中normalizeDate与denormalizaDate函数分别实现数据的归一化与反归一化。

Table 1. Data of handan from 2003 to 2016 on housing sales prices and related factors

表1. 2003年~2016年邯郸房屋销售价格及相关因素数据

3.2. 模型的构建

3.2.1. 网络参数初始化

本文所选BP网络模型为3层网络拓扑结构，网络输入为归一化后的六个因素数据，网络的输出为归一化后的平均房价数据。隐含层与输出层的激活函数分别为tansig函数与purelin函数，评价拟合优度的函数为最小均方函数(LMS)，训练方法则采用具有动量的自适应梯度下降法。

输入层节点数为6，输出层节点数为1，动量系数设定为0.4，学习率设定为0.001，每次训练次数为5000次，报告训练的次数为5次，初始权值与偏置采用系统默认值，其他参数为缺省值。

3.2.2. 隐含层节点数的确定

在理论上，目前还没有一个科学的方法确定隐含层节点数，但在相关的研究中，实验者已经积累了不少可以借鉴的经验。确定隐含层节点数的一个最基本原则是：在满足设定的精度要求前提下，网络结构要尽量紧凑，尽可能取少量的节点。在实际操作中，往往由经验公式给出节点数的大致取值范围，然后再用试凑法确定具体的节点数，网络可以先设定较少(较多)的节点，然后在逐渐的增加(减少)，最终选取训练均方误差最小的隐含层节点数。常用的经验公式为 [3] [4] [5] ：

$m=\sqrt{n+l}+\alpha$

其中：m为隐含层节点数；n为输入层节点数；l为输出层节点数； $\alpha$ 为0~10之间的整数。由前文所述，n的取值为6，l的取值为1，所以m最终的取值范围是4~14。在其他参数不变的前提下，BP网络在不同隐含层节点数目下的训练均方误差由表2给出，最终选取的隐含层节点数为10。

Table 2. Network training mean square errors with different numbers of hidden layer nodes

表2. 不同隐含层节点数目下的网络训练均方误差

3.2.3. 模型训练与仿真结果

本文以R语言为建模工具，利用神经网络AMORE程序包来构建BP神经网络房价预测模型。将邯郸市房价数据分为两部分：2003年至2013年的数据为训练网络所需的训练集，2014年至2016年的房价数据为模型仿真阶段所需的测试集。图2反应了实际值与仿真值的变化趋势，表3内容为实际值与仿真值的比较结果。由表3可知，2014年与2015年的预测误差率分别为0.68%、1.67%，预测结果与实际情况较接近；2016年的预测误差为18.63%，与实际值相差很大。

Table 3. Analysis of BP neural network prediction results

表3. BP神经网络预测结果分析

Figure 2. BP network simulation diagram

图2. BP网络仿真图

4. 小结

在模型仿真阶段，2014与2015年的预测效果较好，误差控制在2%之内，2016年的预测效果不佳，误差为18.63%。对2016年出现的巨大预测偏差结合时政发现，2015年国家出台了一系列有利于购房者政策，如公积金政策的逐步放宽、330新政的出台、降准降息等政策；再结合2016年出现的房地产政策过度宽松、超乎预期的货币宽松政策、经济下行周期下，负利率与资产荒等导致的保值压力、房地产市场回暖的情形下，土地供应搞“饥饿营销”等情况 [6]，不难看出复杂的经济形势以及相关的政策出台对全国房地产市场产生了巨大的冲击。在这样的情形下，2016年邯郸市房地产市场也未能幸免。除了受上述政策等外部环境的影响之外，本文在选取变量因素上采取的主观态度也对预测精度产生了不可忽视的影响。综上所述，2016年房价的实际值与仿真值之间的巨大差异主要是由剧烈的外部环境所导致。

从建模的结果可知，在相对稳定的外部环境下，BP神经网络实现了对邯郸市房价的准确预测，说明BP网络可以作为房价预测的一个有效手段。

NOTES

^*通讯作者。