1. 引言
水道地形测量作为河道资料的主要获取方式,其模式已基本定型于利用GNSS测定点的平面位置,利用测深仪测定点的水深,附之以瞬时潮位或水位资料获得高程,以此确定点的三维坐标 [1]。故水位资料是生产过程控制的关键环节。有关河道观测的水位的获取及推算论述很多,如黄佑生等提出了由上游往下游推求的水面线试算迭代模型 [2];周儒夫等提出了水道水位节点布控和水下测点高程推算方法等 [3] [4];也有采用GNSS测量值作为水位的方法等。但针对具体河段如何选取合理的水位获取方式和推算模型方面的文章较少,为了验证这些不同水位推算方法对水位变化复杂条件下的工程河段水道地形测量精度的影响,笔者选择了宜昌河段的某一区域进行了试验研究,采用不同的软硬件、不同的水位获取方法及推算模型进行对比试验,为水位变化复杂条件下工程河段水道地形观测提供了理论及实践依据,具有较强的针对性、实用性。
2. 水位推算模型与原理
2.1. 线性内插推算模型
对于恒定均匀流量的天然河道 [5],其水面线计算原理基于一维能量方程,然后逐个断面采用直接步进法推求,计算公式如下:
(1)
式中:
、
分别为河道下游、上游断面水位;
、
分别为河道下游、上游断面流量系数;
、
分别为河道下游、上游断面流速;
为重力加速度;
、
分别为上下游河道断面之间的沿程水头损失和局部水头损失。
实际项目生产中,特别是水位不变或均匀线性变化的情况,往往按照上下游(测量区域起止点)断面水位落差和断面布设情况,采用平均落差逐个进行推算。
2.2. 时差法水位推算
大多数测量作业区域的河道水位变化为非线性、非均匀变化,故水位推算也不能简单采用线性内插的方法,这时可以采用时差法水位推算模型。主要原理如下:首先在水道观测一岸的开、收工位置布设水位节点(存在横比降测区可以在河道另一岸合理位置加设水位观测水尺);从水下开始前到结束后按照规定的频次或水位变化的情况进行水位观测。然后根据测量作业布置的中心线法或三点法(也叫区域法)进行水位推算,称之为时差法水位推算。根据不同的条件,可采用二步内插法、平面内插法、距离加权法等进行水位推算,水道观测规范(SL257-2017)给出了具体的推算公式与要求,这里不再赘述。
2.3. GNSS潮位法推算
以上两种方法中,潮位采用了人工或自计水位进行推算。在水道测量时,有时水位通过GNSS测量获得,称为GNSS三维水道观测技术,即利用GNSS观测值作为潮位的模式进行水道地形测量 [6]。
若设H为WGS84参考椭球下大地高,L为GNSS天线高,d为测深系统探头静吃水,T为基于当地基准的当地潮位改正,S为测深系统的测量水深值,ζ为高程异常值,h为基于当地的河底高程。通过相互关系可知 [7]:
(2)
(3)
(4)
若当地基准面为1985国家高程基准面时,ζ为高程异常,此时
高程。则式(4)可转换得到:
(5)
根据项目外业生产可知:S由测深仪实时测得水深,d + L为固定值(钢卷尺丈量),若GNSS接收机实时采集到1985国家高程基准面下的正常高,便可实时测得水下1985国家高程基准的河底高程。
3. 试验布置及数据处理
3.1. 试验实施
本试验选取河段为三峡工程坝下游宜昌河段,一是本河段受水利工程影响水位变化大,且变化过程经常呈非线性变化;二是河道基本比较顺直、河床稳定,底质为山体礁岩构成,测深仪施测过程中其模拟回声效果良好。项目实施区域示意图如图1所示(示意图进行了缩放与旋转调整)。

Figure 1. Schematic diagram of river reach, control distribution and section layout for project implementation
图1. 项目实施河段、控制分布及断面布设意图
1) 控制网布设及转换参数求取
在长约20公里的带状测区内,上中下合理选取3个国家C级控制点,通过测量及解算,求取国家坐标转换七参数,平面及高程转换残差满足CH/T2009-2010标准要求,并对转换参数进行实地检查与校核工作。
2) 水位控制基点测量
在转换参数控制区域内,选择长约5 km左右范围的测量作业区域起止埋设2个水位基点,采用四等水准观测精度联测国家二等水准成果,用作水位施测起算点(河段基本顺直,根据长期资料积累可知,本段不存在横比降情况)。
3) 区域水道地形测量
① GNSS基准站及流动站设置:在水下测量区域中间,架设GNSS基准站,设备系统配置中输入当地坐标系统及求取的七参数,以准确得到当地实时平面坐标与当地基准高程值,流动站接收到基站信息,进行实时改正,并选择已知点进行精度检校。
② 水位控制测量:在水下测量区域的首尾进行水位控制测量,精度达到五等水准精度,同时设立人工水尺和潮位自计仪;在水下测量期间,采用人工和自计两种方式记录水位变化值。
③ 水道地形测量:水下作业前先将测深仪各部件连接、设置、改正及检校。将GNSS天线与换能器采用一体杆连接,确保其在同一垂直平面上,并量取GNSS天线相位中心(或天线底部)到换能器底部之间的距离,同时精确量取回声仪探头吃水深度。
本次试验采用3 × 10 m铁船作为测量船(此船长期在本区域实施测量工作,稳定性较好),在头部约三分之一处左边安装一套中海达测深系统,单独数据采集与处理;右边安装海鹰Hy1601测深系统,海鹰Hy1601作为水深采集单元,将水下和平面数据分别输入Hypack软件和亿点通海洋测量软件,实现全野外一体化、实时同步水道地形测量与数据采集。
水道地形测量采用横断面法,断面方向应大致与水流方向垂直,断面间距为180 m,测点间距取5 m。作业过程中应用Hypack导航测量软件现场严格控制船的走向,随时关注行船的平稳性、GNSS跟踪的卫星数量、卫星图形精度、基站信号和模式及观测精度等情况。三种软件自动记录流动站测得的水面点的平面位置、高程,同步瞬时记录测深仪测得水深值。
④ 为了验证单波束GNSS验潮与船的姿态关系,在试验过程中,将一体化罗经与运动传感器Octans的改正参数输入了亿点通海洋测量软件。
3.2. 数据处理
本次试验数据处理总共得到以下几种数据形式:
1) 采用在水道地形测量开始及结束的位置观测的水位值,按照断面个数及水位落差进行逐个断面水位推算,即线性内插法。
2) 采用Hypack软件按照时间和距离的中心线法(时差法)内插推算模式推算每个断面的水位。
3) 分别采用中海达测深系统自带软件和亿点通海洋测量软件进行处理,得出验潮模式下(时差法)每个断面和每个定标点的水位,以及GNSS验潮模式下的每个断面和每个定标点水位。
4. 水位获取与改正分析
4.1. 试验辅助观测分析
1) 人工水位观测
测量作业期间通过人工和自计的方式对现场水位进行了观测,其变化情况如图2所示。其测量作业期间水位是先上涨、后回落、再上涨的一个变化过程且开始阶段涨幅较大,整个作业期间水位变化达0.5 m左右,是典型的工程调节模式下的非线性变化过程。
2) 声速剖面观测
在测量期间,试验组于上午、中午采用声速剖面仪对测区内进行了两次垂直声速测量,为了便于水深声速改正,测量结果见图3所示。通过观测得知,无论在时间和空间上,其声速变化较小,其影响可以忽略。
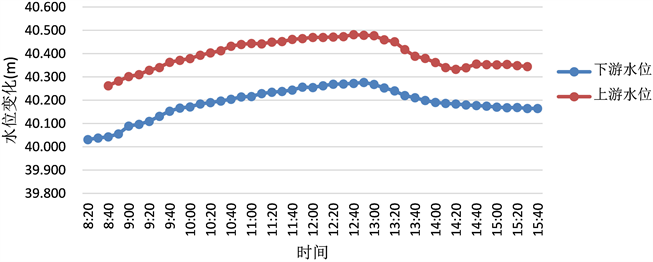
Figure 2. Schematic diagram of water level changes in upstream and downstream during surveying
图2. 测量作业期间上下游水位变化情况图
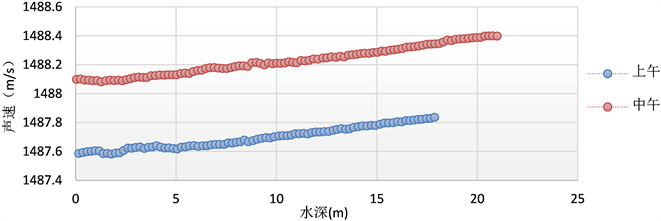
Figure 3. Schematic diagram of sound velocity profile measurement
图3. 声速剖面测量示意图
4.2. 试验数据对比分析
1) 不同测深系统测深对比
为了验证不同测深系统的水深观测值的是否存在差异性,试验组挑选了水下变化情况复杂的SY16号断面进行对比分析,如图4所示。
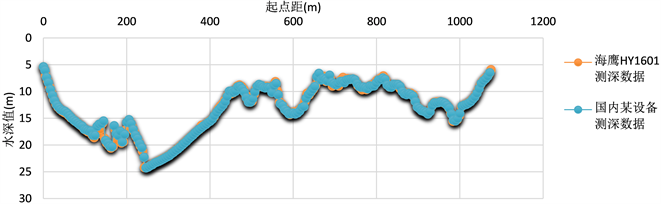
Figure 4. Schematic diagram of synchronized depth observation with different equipment
图4. 不同设备同步水深观测对比图
通过查看现场的模拟回声及后处理回放数据对比分析可知,国内两套测深设备系统观测数据基本无差异,满足水道地形测量生产的需要。
2) 不同水位获取与改正方式对比分析
本次试验采用基于Hypack时差法(时间和距离的中心线法)推算的水位作为基准值,将传统断面个数线性内插法、中海达测深系统和亿点通海洋测量软件处理人工(自计)实测验潮数据(时差法)、GNSS验潮数据分别作对比分析,其结果见图5及表1所示。
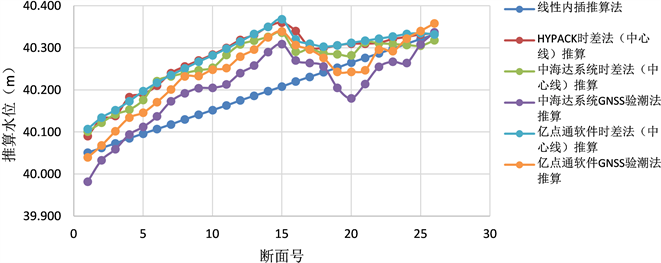
Figure 5. Different water level acquisition methods and comparative analysis sketches
图5. 各种水位推算方法与对比分析图

Table 1. Table for distribution of mutual differences between different water level values and baseline values
表1. 不同水位值与基准值互差分布
为了验证姿态改正对GNSS潮位值的影响情况,实验组对接入姿态仪的亿点通海洋测量软件,在数据后处理时分别进行姿态改正和不改正两种情况数据分析,取其中一个断面进行对比,其结果见图6所示。
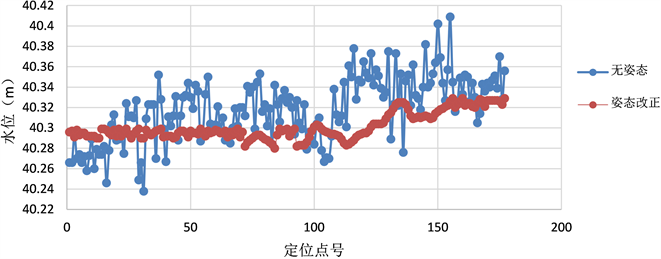
Figure 6. Comparisons between attitude correction and non-correction in a domestic oceanographic survey software
图6. 亿点通海洋测量软件进行姿态改正与不改正之间的比较
从图5、图6和表1可知:
1) 工程调节河段,其水位呈现非线性变化的情况下,不宜采用在水道地形测量开始及结束的位置观测的水位,按照断面个数及水位开始和结束时的落差进行逐个断面水位推算的这种线性内插方法。
2) 不同软件处理系统对数据进行处理,在时差法上对比可知,其互差均小于5 cm,故采用人工(自计)验潮值通过时差法进行水位改正,精度最高且符合实际情况。
3) 中海达测深系统(未接入姿态改正)GNSS验潮值经过粗差剔除及多次滤波处理后,按断面取平均与基准值对比,互差最大值为0.13 m;亿点通海洋测量软件(接入姿态仪)GNSS验潮值进行了姿态改正、粗差剔除及多次滤波处理后,按断面取平均值与基准值对比,互差最大值为0.068 m,且小于5 cm的达80.7%;说明采用GNSS潮位接入姿态改正是很有必要的。
4) 根据《水运工程测量规范》,在水深 ≤ 20 m时,要求水深测量精度σh ≤ 0.2 m,按照水位改正精度为σh的1/3,即≤0.07 m的要求,表明接入姿态仪后,采用合理的处理方法,GNSS三维水深测量可以达到此精度要求。
5. 结论与建议
通过试验及分析表明,不同的水位获取与推算方式,其值会出现较大差别;如果采用的方法不合理,甚至会出现水位值错误,从而导致水道地形测量精度不高的情况发生。所以在水利工程调节影响、水位变化复杂的河段进行水道测量时,水位获取与推算方面建议如下:
1) 结合水道地形测量的项目用途、成图比例尺、测区情况等因素合理选取水位的获取与推算方式,特别是基于非线性变化的河段,其人工(自计)验潮模式下的水位推算方式(时差法,中心线法或区域法)最为可靠,但要注意水位零点的误差传播。
2) 通过对比分析,采用断面平均的GNSS验潮方式(有姿态改正),满足《水运工程测量规范》相关要求,可以根据项目用途及要求合理选取GNSS验潮方式。
3) 试验表明,姿态改正能有效提高GNSS验潮精度。但是在数据处理过程中,要应用软件剔除粗差,选择适宜的GNSS滤波方式及次数。如果是长江这种带状河段,可以优先选取断面平均法作为最终的断面水位。
总之,受水利工程调节影响河段水位获取与改正方法对水道测量精度的影响较大,在类似河段进行水下地形测量时,要充分分析河段特性,选取合理的水位获取及推算方法。
基金项目
本论文为国家重点研发计划专题《堤防工程风险识别和监测预警技术研究(2017YFC1502604)》的分项研究内容。
参考文献