1. 引言
盾构隧道施工中因埋深而受到水土的压力作用,致使管片之间容易产生渗漏现象,对隧道使用功能有严重的影响。盾构隧道管片之间防水是通过预留沟槽嵌套密封垫来达到目的,密封垫的可靠性能决定了隧道的整体质量和安全,重复性的出现渗漏现象,返修时投入人力物力,严重的影响到施工效率和成本 [1] [2] [3]。
随着盾构施工埋深的深度不断增大,密封垫所受的水土压力增大。密封垫可靠性在于所受的接触应力大于水土压力才能起到密封效果,因此针对管片密封垫密封性能的研究对于提高隧道寿命、降低施工成本等具有重大意义。国内外学者对管片密封性能进行了大量研究。Ding [4] 等人研究开发了一套新颖的装置,用以研究在施工和操作阶段,在现场荷载条件下,检测管片密封垫的密封性能及力学行为。Gong [5] 等人采用试验与计算相结合的方法对南京渭三公路隧道(南京渭三公路隧道)进行了密封性与力学性能的研究,建立了密封垫的有限元模型,并对试验结果进行了验证。Shi [6] 等人根据隧道管片接头的使用环境,对三元乙丙橡胶在地下水环境中进行加速老化试验,得出其性能退化规律。根据材料老化后力学性能的变化规律,提出了一种用于管段连接的三元乙丙橡胶垫片的时变本构模型,并利用室内老化试验的结果,得到了材料老化后力学性能的时变参数表达式。Shalabi [7] 等人在静载荷和动载荷作用下,对密封垫的隧道衬砌管片的渗漏特性,设计实验分析不同垫圈材料在水压小于0.9 MPa时的密封性能(氯丁橡胶和三元乙丙橡胶垫圈,带开口底座)。Shalabi [8] 等人研究了槽内垫片的力学性能和密封性能。考虑了两种类型的垫圈:低设计水压的开式底座垫圈和高水压的闭式底座垫圈。重点研究了密封垫在槽内载荷作用下的变形行为和密封垫的密封潜力,包括密封垫接触载荷、松弛、挤压以及水压作用下接头间隙的变化。Li [9] 等人首次对上海地铁13号线采用的纵缝进行了足尺试验,实验中考虑到混凝土、螺栓和垫片对接头力学性能的影响。董林伟 [10] 设计实验研究密封垫两侧侧限材料的不同,对密封垫耐水压力试验的影响。陈云尧 [11] 等人利用ABAQUS软件建立二维模型,采用平均接触压力作为评价指标,分析盾构隧道管片接缝处于不利工况下的失效模式;最后结合橡胶硬度参数、密封垫孔洞参数调整,研究密封垫防水性能改善方法。龚琛杰 [12] 等人在调研国内典型大直径水下盾构隧道的接缝防水构造的基础上,建立接缝弹性密封垫的设计方法,该设计方法由工程参数提取、试验前有限元预分析、试验研究和试验后有限元分析4部分内容构成。最后,应用该设计方法成功指导南京纬三路长江隧道的接缝弹性密封垫设计,证明其科学性和可行性。吴炜枫 [13] 等人以广州深层排水盾构系统东濠涌试验段工程为依托,根据工程实际尺寸1:1制作了弹性密封垫和混凝土试件,进行密封垫防水试验,确保弹性密封垫具有稳定的长期耐高水压性能。
以上研究在试验方面对管片密封垫的分析已经很成熟,但是试验过程繁重且不易操作。因此考虑利用有限元软件对管片密封垫进行密封特性分析。对于隧道安全性能要求,长时间处于高水压的环境中,对密封性能要求更加严格。利用ansys软件,建立管片密封垫的仿真模型,由于模型处于对称结构,故建立二维模型,减少仿真时间,设计方案使密封垫模型在不同的压缩位移下,分析管片密封垫所受接触应力和Von Mises应力,分析管片密封垫的密封性能,为管片密封设计提供理论基础。
2. 工程背景
山西省某引水工程施工设计为单线单洞隧洞,盾构区间起始里程为K52 + 854,终止里程为K47 + 337.1,隧道全长5516.9 m,隧道内径4520 mm,外径5220 mm,设计纵坡1/3000,采用一台泥水盾构自下游向上游掘进。工程标段主要横穿中条山及其北麓,地面高程在530~600 m之间,地形总体沿隧洞出口方向逐渐降低,洞线位于地下水位以下,地下水位高出洞底最大约105 m,也即工作环境地下水最大压力大小为10 bar,且地下水位沿着隧洞出口方向逐渐降低。根据施工地段地质岩土勘察报告,隧道埋深60~100 m,标段地层上部为第四系全新统洪冲积物、下部为第四系上更新统洪积物。盾构法施工的主要隧洞穿越硬岩性为卵石混合土、含砂低液限粘(粉)土。砂卵石的主要成分是片麻岩、混合花岗岩、辉绿岩、角闪岩等,充填物为低液限粉土及中粗砾。施工区间桩号K52 + 854~K49 + 500段以低液限粘土为主,位于地下水位以下0~30 m向掘进方向地下水位逐渐升高;桩号K49 + 500~K47 + 350段以卵石混合土为主,位于地下水位以下30~105 m,其中桩号K47 + 500~K47 + 350位于地下水位90~105 m。
3. 管片橡胶密封垫的参数确定
EPDM(三元乙丙橡胶)橡胶密封垫是国内管片密封的主流材料,一般为多孔性,具有较好的耐压缩性,靠预压缩后产生的回弹力给密封接触面一定压力,当施工中由于管片拼装产生一定的间隙和偏移时,密封垫的密封性能依旧很好。由于实际施工过程中很难对其进行密封性能分析,故建立密封垫模型,利用ansys有限元软件模拟工作状态。现做如下假设 [14] [15] :① 三元乙丙密封垫的材料的弹性模量和泊松比不随着密封垫压缩量改变而改变;② 密封垫在压缩过程中的体积不随压缩而变化;③ 混凝土的弹性模量比密封垫的大很多,将混凝土所做的边界当做刚性边界;④ 不考虑温度对橡胶材料的影响。
针对橡胶材料模型和本构方程,国内外学者已经提出许多用于描述橡胶材料应力应变关系的应变能函数:如Mooney-Rivlin模型、Yeoh模型 [16] [17] Mooney-Rivlin模型可以针对橡胶大变形性能问题提供解决方法,因此本文材料Mooney-Rivlin模型2参数来描述三元乙丙橡胶材料性能。
(1)
式中W为应变能密度,
为Mooney-Rivlin系数,
为第一,第二应力张量不变量。橡胶材料弹性模量 和剪切模量G有如下关系:
和剪切模量G有如下关系:
 (2)
(2)
由于前面已对橡胶材料进行假设,由橡胶材料不可压缩性可得泊松比 ,(2)式可得
,(2)式可得 。
。
剪切模量G与弹性模量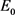 与系数
与系数 的关系为:
的关系为:
 (3)
(3)
结合 的经验比值
的经验比值 ,建立起弹性模量
,建立起弹性模量 与橡胶材料系数
与橡胶材料系数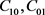 的数学关系。橡胶材料一般情况下橡胶硬度是已知的,根据橡胶硬度HA和弹性模量
的数学关系。橡胶材料一般情况下橡胶硬度是已知的,根据橡胶硬度HA和弹性模量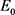 的数学关系式 [18] :
的数学关系式 [18] :
 (4)
(4)
结合上述所列式子由橡胶材料硬度HA便可确定橡胶材料系数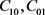 的值,如表1所示。
的值,如表1所示。
4. 管片密封垫模型建立
盾构机隧道施工过程中,需要拼装管片。由于盾构法施工的主要隧洞穿越硬岩性为卵石混合土、含砂低液限粘(粉)土。砂卵石的主要成分是片麻岩、混合花岗岩、辉绿岩、角闪岩等,充填物为低液限粉土及中粗砾,而且洞口位于水平线一下,因此隧道管片密封垫受到较大的水土压力。因此管片密封垫的密封性能直接决定隧道的安全性和使用性。考虑到管片密封垫的结构和受力作用,对实际使用的管片密封垫进行简化建模,建立如图1所示模型。

Figure 2. Geometric dimension of segment gasket
图2. 管片密封垫几何尺寸图
采用二维plane182轴对称单元,使用平面应变的单元行为。管片密封垫与刚体壁面之间设置为面-面接触(Surface-Surface),管片密封垫表面为接触面,使用CONTA172单元模拟,设置该接触单元刚度在每一次迭代计算后基于下伏实体单元的平均应力进行更新,刚体为目标面,使用TARGER169单元模拟。共10,929个节点,11,633个单元,施加载荷为固定下部刚体,对上部刚体施加向下的位移载荷。密封垫的具体尺寸为如图2所示。
5. 管片密封垫密封性能分析
5.1. 管片密封垫压缩理论分析
管片密封垫的形状不是规则图形,而且橡胶受到压缩而变形,其受力跟位移是非线性问题,想要从理论方面直接计算管片密封垫受压变形力计算很难,因此借鉴矩形橡胶压缩弹簧的计算公式,得出管片密封垫的压缩受力计算公式。
根据机械设计手册 [19] 和文献 [20] 中提出矩形橡胶压缩弹簧的计算公式:
 (5)
(5)
中L为橡胶的压缩量,F为压缩力,h为橡胶弹簧自由高度,a为橡胶弹簧的自由长度,b为橡胶弹簧的自由宽度, 为橡胶弹簧表现弹性模量,
为橡胶弹簧表现弹性模量, ,i为橡胶弹簧的几何形状和硬度的影响因子,
,i为橡胶弹簧的几何形状和硬度的影响因子,
 ,S形状因子之比即橡胶承载面积与自由面积之比,
,S形状因子之比即橡胶承载面积与自由面积之比, ,G剪切模量。
,G剪切模量。
对于本文管片密封垫,作出以下假设:① 将管片密封垫视为类矩形,其形状因子S满足: ,η为类矩形形状因子变化系数,范围为0.6~1,随着压缩量变化变化。
,η为类矩形形状因子变化系数,范围为0.6~1,随着压缩量变化变化。
② 忽略受压管片密封垫截面的两侧边受力和变形。
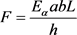 (6)
(6)
根据管片设计资料和管片拼装质量检测标准,选取管片最大的张开量为6 mm,因此压缩量可设计为1、2、3、4、5、6 mm,计算受力为:
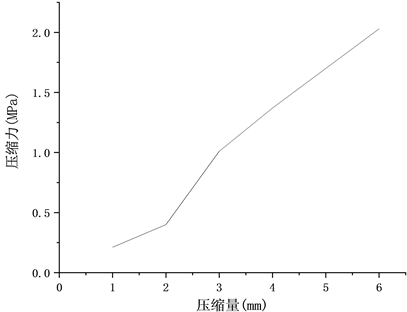
Figure 3. Compression force of segment gasket under different compression
图3. 不同压缩量下管片密封垫所受的压缩力
由图3可得管片密封垫在压缩量为5 mm时的压缩力1.69 MPa,根据作用力与反作用力原则,其反向力大小也为1.69 MPa,大于水土压力时,满足管片密封垫的密封条件,保证了管片密封垫的正常密封性能。
5.2. 管片密封垫仿真分析
Von Mises应力含义是当单元体的形状改变比能达到一定程度,材料开始屈服。接触应力是两个物体互相挤压时在接触区附近产生的应力,反映了管片密封垫的密封能力,当管片密封垫的接触压力不小于水土压力则说明该密封垫的密封性能良好 [21] [22]。
由于本工程隧道位于地下水位以下,地下水位高出洞底最大约105 m,也即工作环境地下水最大压力大小为10 bar,且地下水位沿着隧洞出口方向逐渐降低。管片接缝防水的好坏直接影响着隧道的整体质量和安全。根据管片设计资料和管片拼装质量检测标准,选取管片最大的张开量为6 mm,张开量为两个管片之间的空隙距离。因此本文选取位移载荷梯度为1、2、3、4、5、6 mm。压缩量5 mm所对应的是管片最大张开量6 mm位置。

Figure 4. Maximum Von Mises stress diagram of segment gasket under different compression
图4. 不同压缩量下的管片密封垫的最大Von Mises应力图

Figure 5. Maximum contact stress diagram of segment gasket under different compression
图5. 不同压缩量下的管片密封垫的最大接触应力图
综合图4和图5可以看出,管片密封垫随着压缩量的增大而变形增大,其抵抗变形的应力增大,所以接触应力和Von Mises应力随着压缩量增加而增大。当压缩量为5 mm之后,接触应力和Von Mises应力随着压缩量增大的幅度减小。此时管片密封垫的Von Mises应力为0.562 MPa,接触压力为1.79 MPa。当接触压力大于水土压力时,满足管片密封垫的密封条件,保证了管片密封垫的正常密封性能。
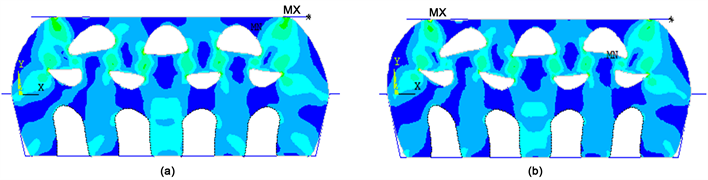
Figure 6. Von Mises stress nephogram. (a) Compression 4 mm; (b) Compression 5 mm
图6. Von Mises应力云图。(a) 压缩量4 mm;(b) 压缩量5 mm
从图6可以看出随着压缩量的变化,Von Mises应力峰值的位置也在发生变化,即说明了在随着压缩量的变化过程中可能出现破坏的位置是不断变化的。
5.3. 管片密封垫受力分析对比
管片密封垫压缩理论分析通过对矩形橡胶压缩弹簧计算公式进行因地制宜化,引入η为类矩形形状因子变化系数,对管片密封垫进行理论计算得出管片密封垫所受的压应力。管片密封垫分析是通过有限元仿真软件对密封垫受压过程进行模拟,得到密封垫的最大接触应力。通过受力分析可得压缩力和最大接触应力是相同的。

Figure 7. Comparison of compression force values of segment gasket under different compression amounts
图7. 在不同压缩量下管片密封垫压缩力值对比图
通过图7可以看出由理论计算所得管片密封垫所受的压缩力与仿真分析具有相同的一致性,从而验证了滚刀密封垫仿真分析的正确性。从图中看出两条线没有完全重合,很大程度是因为所做的假设情况没有考虑到,存在偏差。
6. 结论
1) 通过在矩形橡胶压缩弹簧计算公式的基础上,因地制宜的分析管片密封垫的实际情况,引入η为类矩形形状因子变化系数,从而计算管片密封垫所受的压缩力,为分析管片密封垫密封性能提供理论基础。
2) 以橡胶Mooney-Rivlin本构模型的基础上,采用有限元方法分析了盾构机管片密封垫密封性能,计算了管片密封垫在不同的压缩量情况下管片密封垫所受的最大接触应力和Von Mises应力。管片密封垫所受最大接触应力和Von Mises应力随着自身的压缩量的增大而增大,当压缩量达到5 mm时,最大接触应力为1.79 MPa,满足密封条件,此时达到管片最大张开量。与实际情况相符,可以判断建立的模型的正确性,研究结果管片为密封垫设计提供了理论参考,对盾构机在高水土压力环境中的施工具有重要工程价值。
3) 理论计算跟仿真分析管片密封垫压缩量为5 mm时,密封垫的所受压力为分别为1.69和1.79 MPa相差较小,验证了管片密封垫仿真分析的正确性。管片密封垫仿真分析为管片密封垫密封性能提供了一种可利用的途径。