1. 引言
据联合国发布的《世界人口展望:2015年修订版》报告预测,2050年,中国人口年龄的中位数将由2015年的37岁变为49.6岁,这意味着中国人口结构老化迅速,“人口红利”逐渐消退,人口老龄化问题日益凸显 [1]。国内外学者分析研究了人口老龄化对一国经济社会进步和发展的显著影响 [2] [3] [4] [5],因此对老龄化水平的预测可以为相关政策措施的制定提供依据,进而有效避免人口老龄化的不利影响。
对于预测模型的选择,张振华(2015)以烟台市为例,使用灰色预测模型进行预测 [6] ;而张荣雁等(2013)认为使用残差灰色预测模型对老龄化水平进行预测,其预测效果要优于原始的灰色预测模型 [7] ;陈毅华等(2012)以湖南省为例,运用RBF神经网络模型进行预测,并证明其预测效果较线性回归模型更优 [8] ;黄健元(2010)以江苏省为例,基于Leslie矩阵方程进行预测,并对其诸多特征进行剖析 [9] ;陈光慧等(2014)所选用的预测模型是非参数自回归模型,在证明其比AR(1)模型预测更有效的同时,就我国老龄化现状提出相关的政策建议 [10]。
单一模型虽能较好地预测人口老龄化趋势,但不同的模型在预测方面有各自的优劣,为充分发挥单一模型在预测方面的优势并减弱其劣势,将各个单项模型通过一定的准则赋予一定的权重,而后构建组合预测模型,组合预测模型一直是国内外学者研究的重点,学者们针对不同的问题探讨了该模型的适用性,并证明组合预测模型在预测精度上的确优于单项模型 [11] [12] [13] [14]。然而,几乎没有学者运用该模型对我国人口老龄化水平进行预测,因此为使预测更准确,本文引入组合预测模型进行分析预测。
本文用MATLAB (2016)构建二次指数平滑预测、修正的灰色预测和BP神经网络预测这三个单项模型,而后分别求出样本内预测的误差平方和,进而根据误差平方和倒数法确定权重,构建人口老龄化的组合预测模型,并得出不论是样本内预测还是样本外预测,组合预测模型的预测更有效的结论。而后运用该模型对2017年至2022年我国老龄化水平进行预测,预测结果显示,未来我国人口老龄化问题仍日益严重,基于此,结合我国国情,本文提出以下四点建议:第一,适当提高出生率;第二,大力发展老龄产业;第三,加快城市化发展进程;第四,深化城乡养老制度的改革。
2. 模型简介
2.1. 二次指数平滑预测法
二次指数平滑是在一次指数平滑值的基础上,再进行一次平滑,由于二次指数平滑更充分地利用了样本数据,因此其预测也更为精确 [15],其模型可表述为:
(1)
在式(1)中,
为第t + T期的预测值,
,
。其中,
为平滑系数,对于a的选择须反复试验找到使误差最小的a值;
为一次指数平滑值,
为二次指数平滑值,
为第t期的实际值。
2.2. 修正的灰色预测法
修正的灰色预测法即利用残差对传统灰色预测模型进行修正,修正后其预测误差明显变小 [16],本文所使用的是修正的灰色预测GM(1,1)模型,其建模步骤可表述为以下四步:
第一步,设原始序列为
,构建基于
的灰色预测GM(1,1)模型,其中
:
(2)
第二步,对式(2)求得的
进行一次累减
,即可得到
的预测值
:
(3)
第三步,将
与
之差
作为残差序列,取其尾部部分残差子序列
构建灰色预测GM(1,1)模型。若残差子序列均为正数则可直接构建;若
均为负数则可将其当做正数直接构建,构建后加上负号;若有正有负则应加上最小负数的绝对值,将其转化为正数构建,构建后再减去该绝对值。以均为正数为例,则基于残差子序列的灰色预测GM(1,1)模型如下,此时
:
(4)
第四步,对第三步所求
重复第二步的步骤,得到其预测值,而后即可得到修正的灰色预测GM(1,1)模型:
(5)
在式(5)中,当
时,
取0,反之当
时,
取1。式(5)仅是残差子序列均为正数的情况,若均为负数则“+”变为“−”,若有正有负则“+”不变,在该式末减去残差子序列中最小负数的绝对值。
2.3. BP神经网络预测法
BP神经网络是一种单向传播的多层前向网络 [17],本文选用较为典型的三层结构网络(即包括输入层、隐层和输出层)进行预测,其结构如图1所示。
其建模步骤可表述为以下六步:
第一步,对数据进行无量纲化处理和归一化处理,使输入数据和目标数据落在区间[−1, 1]内;
第二步,隐层神经元个数为
,其中
分别为输入层和输出层的神经元个数,a为常数且
。当然在实际过程中还须不断调整各种参数,力求最优的预测效果;
第三步,创建网络,本文将输入层和隐层的传递函数设定为tansig,即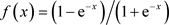 ,输出层的传递函数设定为purelin,训练函数设定为trainlm,权重学习函数设定为learngdf,性能函数设定为mse,仿真函数设定为sim;
,输出层的传递函数设定为purelin,训练函数设定为trainlm,权重学习函数设定为learngdf,性能函数设定为mse,仿真函数设定为sim;
第四步,设定参数,本文设定训练状态的显示幅度为50,学习速率为0.1,动量系数为0.9,训练次数为1000次,误差精度为0.001;
第五步,在训练网络过程中,对阈值和权重反复调整进而减小性能函数mse的数值,在达到预先设定的误差精度时,训练终止;
第六步,利用BP神经网络进行仿真预测并模拟输出数据。
2.4. 组合预测模型
1969年,Bates和Granger开创了组合预测模型方法,是根据一定的准则赋予各个单项模型一定的权重,而后根据权重组合到一起形成的新模型 [18]。该模型权重的设定方法主要有:等权法、简单加权平均法、误差平方和倒数法等,由于前两种方法较为简单,但存在较大的误差,因此本文采用误差平方和倒数法来设定权重。则第i个单项模型的权重可表示为:
(6)
在式(6)中,n为单项模型的总个数,在本文中n = 3,即有3个单项模型;
表示第i个单项模型样本内预测的误差平方和,即有:
(7)
在式(7)中,T表示总年数,
为第t时期的真实值,
为第t时期用第i个单项模型所得的样本内预测值。
越大,第i个单项模型预测误差越大,相应的权重也就越小,反之亦然。
求出各个单项模型的权重后,建立组合预测模型如下:
(8)
在式(8)中,
为组合预测模型第t期的预测值,以本文为例,
、
和
分别为三个单项模型在第t期的预测值,
、
和
分别是三个单项模型根据式(7)所求得的权重。
3. 组合预测模型预测的有效性分析
3.1. 组合预测模型的构建
3.1.1 数据来源
本文选取我国1978年至2016年人口老龄化指标数据(本文中老龄人口指的是我国65岁及以上人口,人口老龄化指标数据即为其与我国总人口之比)。为研究组合预测模型预测的有效性,本文将1978年至2010年的人口老龄化数据作为样本内数据,将2011年至2016年的人口老龄化数据作为样本外数据,以此分析组合预测模型与三个单项模型样本内预测与样本外预测的有效性。
3.1.2. 构建单项预测模型
本文为计算出构建组合预测模型的各个单项模型的权重,使用MATLAB (2016)构建三个单项模型,并分别得出样本内预测的误差平方和。
1) 二次指数平滑预测
对于二次指数平滑预测,a的取值对预测精度有一定的影响,分别令a为0.1、0.3、0.5、0.7、0.9,进而选取使误差平方和最小的a,对于不同的a其样本内预测的误差平方和如表1所示。

Table 1. The sums of squared error within the sample forecast by the different values of a
表1. 不同a的样本内预测的误差平方和
由表1可以看出,当a为0.5时样本内预测的误差平方和最小,因此本文令a为0.5,其样本内预测的误差平方和为2.7238。
2) 修正的灰色预测
对于修正的灰色预测,本文选取
,此时残差的子序列有正有负,则应加上最小负数的绝对值,将其转化为正数构建,构建后再减去该绝对值。所构建的模型如下:
当
时,
;
当
时,
。
而后可以求得,其样本内预测误差为2.5643。
3) BP神经网络预测
对于BP神经网络预测,输入变量为人口老龄化指标数据,本文令输入层的神经元个数为5个,输出层为1个,则隐层神经元个数为4~12个。经训练,当隐层神经元个数为9时,误差最小。此时,其样本内预测的误差平方和为1.7641。
3.1.3. 构建组合预测模型
由上述求得的误差平方和,根据式(6)得出三个模型的权重分别为0.2773、0.2946、0.4281。则所构建的组合预测模型如下:
(9)
在式(9)中,
为组合预测模型第t年的人口老龄化组合预测值,
、
和
分别是三种单项模型第t年的人口老龄化预测值。
3.2. 预测的有效性分析
1) 预测有效性的评价指标选取
本文选取预测的均方误差(mean square forecast error,简称MSFE)作为预测有效性的评价指标,其计算公式如下:
(10)
在式(10)中,T表示预测的样本总数,
表示实际值,
表示预测值。MSFE越小,说明
与
的差异越小,该模型的预测越有效。
2) 样本内预测的有效性分析
利用三个单项模型以及建立的组合预测模型对1978年至2010年的人口老龄化数据进行样本内预测,得到1978年至2010年四个模型的样本内预测值,而后由式(10)分别计算出MSFE,MSFE的数值表2所示。

Table 2. The comparison of MSFE within the sample forecast in four forecasting model
表2. 四个预测模型样本内预测的MSFE比较
由表2可以看出,一方面,基于三个单项模型构建的组合预测模型的MSFE最小,因此其样本内预测最有效;另一方面,在三个单项模型中,BP神经网络的样本内预测最有效,其次是修正的灰色预测,样本内预测能力最差的是二次指数平滑预测。
3) 样本外预测的有效性分析
通过样本内预测难以反映模型对未来的预测能力,而样本外预测可以对模型预测的有效性进一步分析,组合预测模型虽然在样本内预测的精度最高,但并不意味着对未来也有最好的预测能力。因此为选择最优模型使对未来的预测更精确,本文对2011年至2016年的人口老龄化水平进行样本外预测,所求得的MSFE的数值如表3所示。

Table 3. The comparison of MSFE outside the sample forecast in four forecasting model
表3. 四个预测模型样本外预测的MSFE比较
由表2、表3可得出如下结论:第一,无论是样本内预测还是样本外预测,组合预测模型的MSFE在四个预测模型中最小,因此组合预测模型在对人口老龄化的预测方面具有一定的有效性;第二,在三个单项模型中,无论是样本内预测还是样本外预测,BP神经网络的预测精度最高,其次是修正的灰色预测,预测能力最差的是二次指数平滑预测;第三,对于模型预测有效性的研究主要是研究模型对未来的预测能力,虽然在此例中样本内和样本外的预测精度排名相同,但实际上,样本内预测精度高的模型对于样本外预测精度的高低是不确定的,因此在分析预测有效性的问题时,应在样本内预测精度合理的前提下较多地关注样本外预测的有效性。
4. 我国人口老龄化预测
根据组合预测模型有效性的实证分析,可以得出:组合预测模型在样本内、样本外预测均具有有效性,因此可利用该模型可以对中国未来几年人口老龄化水平进行预测。为提高预测的准确性,令1978年至2016年作为样本内数据,构建单项模型,然后得到新的权重,分别为0.2952、0.3239、0.3809,则构造组合预测模型如下:
(11)
根据式(11)对2017年至2022年我国老龄化水平进行预测,预测结果如表4所示。

Table 4. Foercast of China’s aging of population from 2017 to 2022
表4. 我国2017年至2022年人口老龄化水平预测
由于我国在2000年正式步入老龄化国家,虽然步入时间较晚但发展速度过快,因此我国老龄化问题引起了国内外众多权威机构的关注,并对此做出相关预测,联合国预测2020年中国人口老龄化水平在11.5%左右,国务院发展研究中心预测2020年中国人口老龄化水平在12%左右。由表4可知,运用组合预测模型预测2020年我国人口老龄化水平为11.7936%,介于联合国和国研中心的预测值之间,比较符合实际。因此,运用组合预测模型对我国老龄化水平预测具有指导意义和实践意义。
由表4也可看出,我国人口老龄化问题仍不断加剧,而且并没有减缓的态势,为避免人口老龄化对我国发展的不利影响,政策制定者应对老龄化水平进行合理预测,并制定相关的政策措施以避免其不利影响。
5. 结论与政策建议
本文首先通过构建人口老龄化的二次指数平滑预测、修正的灰色预测和BP神经网络预测这三个单项预测模型,分别求出样本内预测的误差平方和,而后根据误差平方和倒数法确定权重,构建人口老龄化的组合预测模型进行实证分析,并得出不论是样本内预测还是样本外预测,组合预测模型的预测更有效的结论。这是由于组合预测模型是多个单项模型的加权模型,克服了单一模型的缺点,同时又综合了各个模型的优点,因此该模型对我国人口老龄化水平的预测更有效。
由于组合预测模型在人口老龄化水平的预测上具有有效性,因此利用该模型对我国2017年至2022年老龄化水平进行预测,预测结果显示,未来我国人口老龄化问题日益严重,基于此,结合我国国情,本文提出以下四点建议:
第一,由于人口老龄化会导致劳动力的供给不足,适当提高出生率是很有必要的,2016年1月1日我国正式实行“放开二孩”政策,这一政策的实行将有助于弥补老龄人口过多造成的缺乏劳动力等相关问题,但要把握这一政策的“度”,避免“婴儿潮”和劳动力短缺。
第二,大力发展老龄产业,由于老龄产业大多属于第三产业,推动老龄产业的发展有助于推动我国产业结构的优化升级,既满足老年人口的需求,又能减轻年轻人的养老负担、提供就业,与十八届三中全会党中央提出的发展老龄产业的政策相适应,将日益凸显的人口老龄化问题的不利影响转变为产业结构优化升级和经济转型的动力。
第三,加快城市化的发展进程,鼓励农村剩余劳动力参加工作,既可以解决老龄化水平的提高所带来的劳动供给不足的问题,又可以推动城乡一体化发展。2017年4月1日,设立雄安新区为国家级新区,引领未来深度城市化,我国应顺应时代发展潮流,把握机遇,妥善解决人口老龄化所引发的一系列问题。
第四,深化城乡养老制度的改革,是全面深化改革的重要内容,同时也是应对日益严重的人口老龄化问题的重要举措,由于人口老龄化的不断加剧,老龄人口不断增多,对于城乡老龄人口的保障显得尤为重要,通过建立覆盖城乡的养老体系,提高全社会的效率性和公平性。
自2000年我国正式成为老龄化国家后,人口结构老化迅速,“人口红利”逐渐消退,人口老龄化问题日益凸显,根据本文预测,未来老龄化水平仍不断加剧,这就需要政策制定者制定相应的政策措施,有效避免老龄化的日益严重对我国发展的不利影响。