1. 引言
对于某一类特殊的矩阵,很多学者和专家都会关注其子矩阵或者其他相关矩阵是否具有类似的性质或者其他特殊的性质。自Schur补的概念提出之后,对于一些特殊矩阵的Schur补的研究与分析从未间断过。文献 [1] - [6] 中证明了M-矩阵、H-矩阵、严格对角占优矩阵、严格双对角占优矩阵、块对角占优矩阵、严格 对角占优矩阵的Schur补以及diagonal-Schur补都有与原矩阵类似的性质。文献 [7] [8] 给出了矩阵的三角Schur的定义,并证明了严格对角占优矩阵和严格双对角占优矩阵的三角Schur补依然能够保持原局长的特殊性质。本文将参考以上文献的思路以及方法,对广义严格双对角占优矩阵的三角Schur补的一些特殊性质进行分析与讨论,并得到广义严格双对角占优矩阵的三角Schur补是严格对角占优矩阵的结论。
对角占优矩阵的Schur补以及diagonal-Schur补都有与原矩阵类似的性质。文献 [7] [8] 给出了矩阵的三角Schur的定义,并证明了严格对角占优矩阵和严格双对角占优矩阵的三角Schur补依然能够保持原局长的特殊性质。本文将参考以上文献的思路以及方法,对广义严格双对角占优矩阵的三角Schur补的一些特殊性质进行分析与讨论,并得到广义严格双对角占优矩阵的三角Schur补是严格对角占优矩阵的结论。
2. 预备知识
为方便描述与讨论,用n表示大于1的整数,N表示集合
, 表示
表示 阶实矩阵。
阶实矩阵。
设
为n阶复方阵,
。记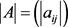 ,
,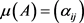 ,其中
,其中
记
,
。
定义1 [9] 设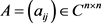 ,如果对所有
,如果对所有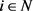 ,有
,有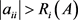 。则称A是一个严格对角占优矩阵。记作
。
。则称A是一个严格对角占优矩阵。记作
。
定义2 [4] 设
,如果对所有的
,有 ,则称A是一个严格双对角占优矩阵。记作
,则称A是一个严格双对角占优矩阵。记作 。
。
定义3 [10] 设
,如果存在
,使得 ,
,且
,
,且
其中 ,
,
。
,
,
。
则称A是一个广义严格双对角占优矩阵。记作 。
。
定义4 [11] 设 ,如果
,其中
,且
,
为矩阵B的谱半径,则称A为M阵。如果
为M阵,则矩阵A称为H阵。
,如果
,其中
,且
,
为矩阵B的谱半径,则称A为M阵。如果
为M阵,则矩阵A称为H阵。
对于 ,
表示N的一个非空子集,
表示
相对于N的补集
,
表示
的势。对N的非空子集
,
表示N的一个非空子集,
表示
相对于N的补集
,
表示
的势。对N的非空子集 ,
,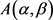 表示一个以
为行指标,以
为列指标的子矩阵;
表示一个以
为行指标,以
为列指标的子矩阵;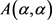 简记为
简记为 。
。
设
,
, 称为A和B的Hadmard积。
称为A和B的Hadmard积。
定义5 [4] 设
,
是N的一个子集且
是一个非奇异矩阵,称
为矩阵A对应于
的Schur补,记为
或
。
定义6 [6] 设
, 是N的一个子集且
是一个非奇异矩阵,称
是N的一个子集且
是一个非奇异矩阵,称
为矩阵A对应于
的对角-Schur补,记为 或
。
或
。
定义7 [12] 设
, a 是N的一个子集且
是一个非奇异矩阵,称

为矩阵A对应于 的三角-Schur补,记为
的三角-Schur补,记为 或
。
或
。
显然,当
时,矩阵A对应于
的三角-Schur补即为矩阵A对应于
的diagonal-Schur补;当
时,我们给
取其定义域内的一些固定值,就可以得到一些不同的三角-Schur补。
3. 主要结论
在证明广义严格双对角占优矩阵的三角-Schur补之前,首先给出一些证明过程中将会运用到的基本引理:
引理1 [10] 如果A是一个广义严格双对角占优矩阵,则
是严格对角占优矩阵。其中,
表示位于矩阵A中标号
的诸行与标号
的诸列的主子阵。
引理2 [13] 如果
是一个H-矩阵,那么
(1)
引理3 [9] 如果A是一个严格对角占优矩阵,则A是一个非奇异H阵。
引理4 [14] 如果A是一个广义严格双对角占优矩阵,则有
或
。
定理1 若
是广义严格双对角占优矩阵,如果
或
,那么A的三角-Schur补
是严格对角占优矩阵。
证明:令
1) 若
,则有
因为A是广义严格双对角占优矩阵,由引理1可知
是严格对角占优矩阵,故 为H阵。
为H阵。
对于
,由式(1)可得
(2)
可知

其中,
,
,由于A是广义严格双对角占优矩阵,由定义有
由引理4可知,当
时,有:
或当
时,有
(4)
由式(3)与(4)有: 为
阶严格对角占优矩阵,
为
阶严格对角占优矩阵。且
为
阶严格对角占优矩阵,
为
阶严格对角占优矩阵。且
进一步由引理5可得:
(5)
结合式(2)与(5),对
,有
因此
是严格对角占优矩阵。
2) 当 时,可以类似得证。
时,可以类似得证。