印刷体数学公式识别研究

Research on Identification of Printed Mathematical Formula

摘要: 随着电子书产业的发展，OCR技术(光学字符识别)的应用越来越广泛，但公式识别还未普及，主要原因是公式本身缺乏规律，同时，论文查重越来越严，也给公式识别提出了新的要求。本文主要研究以图片形式呈现的印刷体数学公式识别，字符分割方面采用了投影行分割和连通域分割相结合的方法，字符识别采用了模板匹配法，然后利用字符的相对位置进行结构分析。系统采用的分割方法在保证运算速度的同时提高了分割精度，对可分割的字符效果好。采用的字符识别方法充分利用了印刷体数学字符的规律性，算法简单，运算复杂度较低，识别精度高于97%。结构分析上考虑了常见的公式结构，分类讨论不重不漏。系统能识别清晰的印刷体数学公式，运算复杂度和字符粘连问题还需要进一步优化。

Abstract: With the development of the e-book industry, the application of OCR technology is becoming more and more widespread, but formula recognition has not been popularized. The main reason is the lack of regularity of formula. At the same time, the paper review has become more and more strict, and it has also proposed new formula recognition claim. This paper mainly studies the recognition of printed mathematical formulas in the form of pictures. For character segmentation, a combina-tion of projection line segmentation and connected domain segmentation is used. For character recognition, template matching is adopted, and then the relative positions of characters are used for structural analysis. The segmentation method adopted by the system improves the segmenta-tion accuracy while ensuring the operation speed, and has a good effect on the segmentable char-acters. The adopted character recognition method makes full use of the regularity of printed mathematical characters. The algorithm is simple with the low computational complexity, and the recognition accuracy is higher than 97%. The common formula structure is taken into account in structural analysis, and the classification discussion is without repetition or omission. The system can identify clear printed mathematical formulas, and computational complexity and character sticking problems need to be further optimized.

1. 引言

信息技术的进步，促进了电子书产业的蓬勃发展，电子书内容的识别与应用的需求也越来越高。OCR技术，即对文本资料进行扫描后对图像文件进行分析处理，获取文字及版面信息的过程，其提出至今已有近90年，在中文材料和英文文章中均已得到广泛的应用。然而，在对数学公式的识别上还未普及，论文查重中还未能对数学公式进行识别，而这正是一些理工科论文的核心内容，同时，当前国内对论文查重的要求越来越高。因此，数学公式的识别与检索对于信息快速共享和预防学术不端现象具有非常重要的现实意义 [1]。

与普通文本识别不同的是，数学公式的分布呈二维状态，其分布无序，而普通文本的分布一般呈现一维状态，同时，对于英文单词的识别，还可通过语义与单词规律进行校正。这使得数学公式的识别更加困难。一般而言，数学公式的识别分为图像预处理、字符分割、字符识别、结构分析、错误纠正、输出几个步骤。因此，本文将主要从前面五个部分进行介绍。

2. 印刷体数学公式识别研究

本文的研究对象是以图像形式存储的印刷体数学公式，一般由PDF文件或对公式截图获得。因此，在进行字符分割与识别之前，需要进行图像预处理。

2.1. 图像预处理

首先将RGB图像进行灰度化处理，常见的灰度化处理有分量法、最大化法、平均法及加权平均法。系统采用MATLAB的内置函数rgb2gray，加权平均法：

$X=0.2989R+0.5870G+0.1140B$

其中X为灰度图像的像素值，R、G、B分别是红绿蓝三种颜色的亮度值。

对得到的灰度图像二值化处理，图像的二值化处理将直接关系到识别的成功与否，同时还关系到字符分割，字符的粘连与分离。常见的二值化阈值选取方法可分为静态和动态，局部和全局，静态常见的有均值法，直方图双峰法等。通过对几种方法的效果对比，最终选取直方图双峰法，并通过多次测试，将二值化阈值设为190，为方便计算，将0~255转换为0~1。

2.2. 字符分割

常见的字符分割方法有投影分割法和连通域分割法。

2.2.1. 投影分割法

投影分割法分为竖直投影分割和水平投影分割，以水平投影分割为例，其通过计算每行没有像素点的数量，对一行中没有像素点的位置进行切割，通过水平投影，可以计算一幅图像的行数，及每一行的高度。水平投影分割的结果见图1。

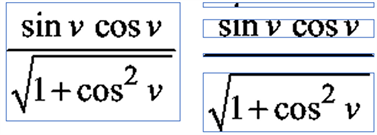
Figure 1. Horizontal projection segmentation

图1. 水平投影分割示例

竖直投影分割同理，其通过计算每一列没有像素点的数量，对一列中没有像素点的位置进行切割，通过竖直投影分割，可以计算一幅图像的列数，及每一列的宽度。竖直投影分割的结果见图2。

Figure 2. Vertical projection segmentation

图2. 竖直投影分割示例

可见，投影分割法操作简单，计算复杂度低。然而，其无法分割嵌套结构，如图3：

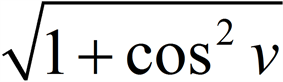
Figure 3. Projection segmentation cannot segment nested structure

图3. 投影分割无法分割嵌套结构例子

而连通域分割法可以处理这种字符。

连通域分割法 [2]，指自上而下搜索第一个有像素的点 $\left(x_0,y_0\right)$，集合 $\text{X}=\left\{\left(x_0,y_0\right)\right\}$。继而搜索它附近的八连通邻域，若其八连通邻域的某个点 $\left(x_1,y_1\right)$ 处有像素，则将这个点纳入集合X中，即 $\text{X}=\left\{\left(x_0,y_0\right),\left(x_1,y_1\right)\right\}$。继续搜索集合X内其他点的八连通邻域(如图4)，一轮结束后，将八连通邻域有像素的点的坐标存储在X中，将有像素的点清除，再继续迭代搜索集合X中其他点的八连通邻域，将有像素的点的坐标存储在X中，直到X不再更新。

Figure 4. Eight connected neighborhoods

图4. 八连通邻域

算法过程见表1。

Table 1. Connected domain segmentation algorithm

表1. 连通域分割算法

执行算法的结果见图5：

Figure 5. Connected domain segmentation

图5. 连通域分割示例

2.2.2. 系统字符分割法

由上可以得知，投影分割法操作方便，计算复杂度低，节约运算资源，但不能处理嵌套结构，而连通域分割法处理灵活，可处理多种复杂公式结构，缺点是迭代循环造成计算复杂度高。因此，结合两种算法，系统决定先对输入的结构利用水平投影分割法分割成多行，再分别对每一行利用连通域分割法分割。使得在处理多种复杂结构的同时降低计算复杂度。

2.2.3. 系统字符分割结果

通过两种方法相结合的分割方法，能够结合两者的优点，分割效果较好，且节约运算资源，能够分割所有理论上能分割的字符。但不能分割粘贴字符，造成粘贴字符不能分割的原因有两种：

一种是组合字符，如积分符合与积分上下限，如图6所示：

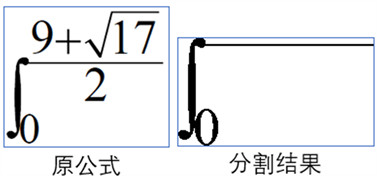
Figure 6. Combining characters cannot be segmented

图6. 组合字符无法分割示例

由于原公式中积分符号与上下限为组合符号，故视为不可分割，对于这种类型的字符，采用添加相关字符进入模板库，主要有： ${{\displaystyle \int }}_0^{\infty }$ 型(主要是0~9，−，∞的有序组合)，dx等。

或平行字符，如图7。

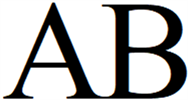
Figure 7. Conglutination caused by parallel character

图7. 平行字符粘连示例

另外一种是由于图像预处理造成的字符粘连，如图8：

Figure 8. Conglutination caused by image processing

图8. 图像预处理造成的字符粘连示例

而最常见的字符粘连，是图9这种情况：

Figure 9. Commonconglutination

图9. 常见的字符粘连示例

2.3. 字符识别

由于研究对象是印刷体数学公式，其具有固定结构，不似手写字符般多变。因此，在识别之前，结合实际，对字符建立模板库。

2.3.1. 模板库建立

印刷体数学公式具有固定的形式，所以，在建立模板库时，以精准、全面为目标，考虑常见的字体等形式，通过以下规则建立模板库，见表2。

Table 2. Requestof drawing template library

表2. 模板库构建要求

为尽量减少信息损失，建立模板库的过程见图10：

Figure 10. Process of drawing template library

图10. 模板库建立过程

2.3.2.字符识别算法

常见的OCR识别算法有模板匹配法，支持向量机法，人工神经网络法，但人工神经网络要求模板数据量较大，适用于手写字符识别 [4]。而识别对象是有固定规律的印刷体，所以系统使用模板匹配法。

1) 特征提取

特征提取指，预处理后，提取公式字符的特征，并用数值进行表示，要求该特征应尽量体现该字符区别于其他字符的不太特点，且体现的特征尽量不交叉。对公式字符提取的特征常见的有：宽高比、孔洞数、网格特征、穿越线等。由于本系统的字符库建立力求精准全面，所以，在考虑特征提取时，考虑对字符大小归一化到16 × 16的256维数据作为特征。

字符大小归一化即图片的缩放。常见的放大缩小算法有最近邻插值算法，双线性插值算法，双三次插值算法。为提高缩放精度，采用双三次插值算法。

双三次插值 [3] 是二维空间中最常用的插值方法。假设源图像A大小为 $m\times n$，缩放后的目标图像B的大小为 $M\times N$。根据缩放比例可以得到 $B\left(X,Y\right)=A\left(x\times \left(M/m\right),y\times \left(N/n\right)\right)$。其可能为浮点数，考虑任意像素点的坐标 $P\left(x+u,y+v\right)$。其中 $x,y$ 分别表示整数部分， $u,v$ 表示小数部分。考虑P点附近的16个像素点的位置(如图11)，用 $a\left(i,j\right),\left(i,j=0,1,2,3\right)$ 表示。

Figure 11. Locationof 16 neighborhoods

图11. 16邻域位置

计算 $a_{ij}$ 的权值 $k_{ij}$。以 $P_{mn}\left(x+u,y+v\right)$ 为例，首先计算

$k_{m0}=W\left(1+u\right),k_{m1}=W\left(u\right),k_{m2}=W\left(1-u\right),k_{m3}=W\left(2-u\right);$

$k_{n0}=W\left(1+v\right),k_{n1}=W\left(v\right),k_{n2}=W\left(1-v\right),k_{n3}=W\left(2-v\right);$

则 $k_{ij}=k_{mi}\ast k_{nj}$。其中W(x)为BICUBIC函数，如下：

$W\left(x\right)=\{\begin{array}{l}\left(a+2\right){\left|x\right|}^3-\left(a+3\right){\left|x\right|}^2+1,\left|x\right|\le 1\\ a{\left|x\right|}^3-5a{\left|x\right|}^2+8a\left|x\right|-4a,1<\left|x\right|<2\\ 0,其他\end{array}$

其中，a取−0.5。

则P点像素值为 $B\left(X,Y\right)={\displaystyle {\sum }_{i=0}^3{\displaystyle {\sum }_{j=0}^{3}A\left(i,j\right)k_{ij}}}$。

为了提高识别精度，在归一化前后进行以下优化/处理：

• 归一化之前，将字符通过加白边的形式扩展为方阵，如图12：

Figure 12. Extendto square matrix

图12. 扩展为方阵

• 对于类似于“,”等大小小于等于5*5的字符，归一化到5*5，这样能防止小字符放大后信息损失太多；

• 以灰度值存储归一化后的数据。

2.3.2. 字符识别

采用模板匹配法进行字符识别，即计算待识别字符X的16*16维数据与模板库中的字符Y的欧式距离，选取距离最小的模板库字符的类别作为X的类别。即：

$d\min {\left(\underset{i=1}{\overset{m}{{\displaystyle \sum }}}\underset{j=1}{\overset{n}{{\displaystyle \sum }}}\sqrt{{\left|X\left(:,:\right)-Y_{ij}\left(:,:\right)\right|}^2}\right)}_{\min }$

${\text{label}}_X=1_{\left(d_{ij}=d_{\min }\right)}\times i$

其中i指第i种字符，共m种字符；j指字符i的第j种形式，共n种。

2.3.3. 字符识别结果

通过随机挑选一部分公式数据(公式量大，覆盖字符多)，进行字符识别，得到结果见表3：

Table 3. Character recognition experiment

表3. 模板库构建要求

从以下实验中可以发现，识别错误的情况主要出现在字符l上，一方面，数字1与小写字母l相似度太高，另一方面Calibri字体下l与|雷同。

2.4. 结构分析

结构分析，即将识别后的字符，利用字符的相对位置，建立公式规则，重组为公式，并用latex语言进行表示。

2.4.1. 位置信息

由于结构分析主要利用的信息是字符的类别和字符的二维结构，因此，在进行结构分析之前，需要对字符的位置进行标记，由于公式的分割是先行投影分割后连通域分割，因此对字符的储存方面采用树结构，每一行为结点，行内分割后的单独字符作为子节点，如图13所示：

Figure 13. Row formula tree

图13. 行公式的树结构

首先记录行节点的行信息：该行所在的上下界，如图14所示：

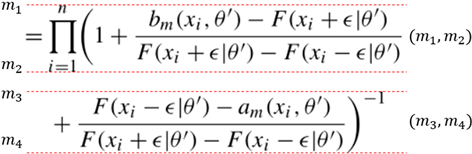
Figure 14. Boundary line location of row formula

图14. 行公式的上下界位置

然后记录单个字符的位置信息，以水平向右和水平向下建立坐标系，记录字符的左上角和右下角坐标 $\left(x_1,y_1,x_2,y_2\right)$。如图15所示：

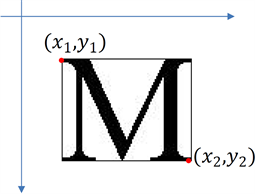
Figure 15. Location imformation of single character

图15. 单个字符的位置信息

结构分析时分两种情况讨论：组合字符和独立字符。首先讨论组合字符。

2.4.1. 组合字符的结构分析

组合字符指由两个或两个以上字符组成的字符，如：“=”，“≈”，“÷”，“±”，“≤”，“，”，“I”，“j”，“!”等。对于这种字符，需要根据字符之间的相对位置确定实际字符。以分析“=”为例，若遇到字符“−”或“ $\frac{}{}$ ”，则判断下一个字符是否是“−”或“ $\frac{}{}$ ”，且下一个字符处于上一个字符的正下方，代码见图16：

Figure 16. The code of judging “=”

图16. “=”判断代码

2.4.2. 独立字符的结构分析

对于独立字符，主要考虑字符之间的相对位置，及特定公式的结构，常见的有分数结构，根号结构，积分结构，乘方/下标(上下限)结构，极限结构。如图17：

Figure 17. Familiarformulastructer

图17. 常见公式结构

考虑分数结构。

1) 分数公式分析

对于分数结构，首先检测是否有“ $\frac{}{}$ ”或“−”，(下记“ $\frac{}{}$ ”)若存在，记录“ $\frac{}{}$ ”的左右边界 $y_1,y_2$，接着判断分数线上下位置是否存在字符，值得注意的是这里要按分数线与分子分母是否处于同一行分情况讨论(这里的同一行是指投影行分割的行)，按照系统的分割法，投影行内字符将按自上而下顺序存储，如投影行数据 $\frac{x}{2y}$ 的字符储存顺序是： $\frac{}{},2,x,y$。因此可以按顺序检索。判断依据参考图18：

Figure 18. Familiarformula structer

图18. 常见公式结构

若分数线上下位置存在字符，则将字符组合为分数，用latex语言表示为'\frac{x}{2x+y}。原来分子分母的字符清空，并对原来分子分母内的字符迭代公式规则判断。

2) 根号公式分析

根号公式相对比较简单，因为根号公式一定处于同一行，且字符之间的相对顺序有序，遇到根号时，首先记录根号的右边界位置y，判断其后的字符的右边界是否小于y，若是，则为被开方数，直至大于右边界y，即图19所示：

Figure 19. Right boundary of radical

图19. 根号右边界

3) 上下标公式分析

乘方，下标，积分上下限属于同一种结构，可以类比分析，这里以乘方为例，进行分析。以 $x^3$ 为例(见图20)，当检索到字符“3”(记为B，其前一个字符为A)时，判断字符“3”是否满足以下条件：

$\{\begin{array}{l}B\cdot y_1>A\cdot y_2\\ B\cdot x_1<A\cdot x_1\\ B\cdot x_2<A\cdot x_1+\left(A\cdot x_2-A\cdot x_1\right)/2\end{array}$

Figure 20. Locationanalyse of superscript

图20. 上标位置分析

值得注意的是B的下一个字符也可能在上标位置，因此，在满足上述条件下，要对B的下一个字符，继续判断上述条件。

4) 标注符号结构分析

在概率统计中，可能会出现类似于平均数 这样的标注符号，下面以最常见的平均数结构为例，在遇到“−”时(在排除“=”和分数情况后)只需判断其正下方的位置是否有字符，且二者高的比例小于1:3即可。见图21：

Figure 21. Locationanalyse of markedsymbol

图21. 标注符号位置分析

5) 上下结构特殊公式分析

上下结构的特殊公式指形如图22中所示的上下结构的公式：

Figure 22. Formulaof up-down structer

图22. 上下结构公式

以极限符号为例进行分析。若遇到连续的三个字符“lim”时，判断其正下方是否有字符“→”，且判断两者之间的相对位置，一般有以下两种情况，见图23：

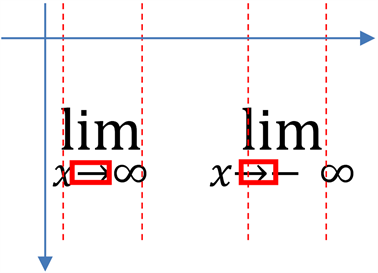
Figure 23. Relative location analyse of “→” in “lim”

图23. “lim”中“→”的相对位置分析

即：

$\begin{array}{l}whento.x_1<\max (l.x_2,i.x_2,m.x_2),\\ countif\\ l.y_1<to.y_1<m.y_{2}orl.y_1<to.y_2<m.y_2\end{array}$

需要注意“lim”与“→”是否在同一个投影行，与极限数的个数。

2.4.3. 公式识别结构

通过以上过程，对部分公式样本进行实验，得到的识别结构较好，举例如下(见图24和图25)：

Figure 24. Eg.1 Formula recognization

图24. 公式识别示例1

Figure 25. Eg.2 formula recognization

图25. 公式识别示例2

3. 评价与展望

本系统采用的分割方法在运算速度和分割精度之间取得平衡，利用印刷体字符的规律性，以精准为模板建立字符模板库，并采取简单高效的模板匹配法进行识别，识别精度高，对于识别错误的字符追根溯源，找到识别错误的原因(字符高度相似如1和l，模板库字符形态相似)，并针对性处理，采用的公式规则逻辑性强，覆盖性全，识别效果较好。但是由于字符粘连的情况无法分割导致识别错误的情况发生，因此对识别效果产生一定影响。同时对印刷体书写原因造成的字符粘连采用的扩充模板库方法，还未涵盖所有情况。因此，本系统对字符间距非特别小的情况识别较好，同时识别时间还需要进一步优化。

参考文献