轨道车辆防滑器检测判据对防滑性能影响的仿真研究

Simulation Study on the Impact of Rail Vehicle Skid Detection Criteria on Skid Performance

摘要: 本文以列车单轮对系统为例，设计了一组合理的轮轨黏着模型，从制动距离和耗风量指标出发，在低黏着轨面、紧急制动工况下，研究防滑器滑行检测判据改变对列车防滑性能的影响，涵括滑行检测里的减速度判据、速度差判据以及滑移率判据。研究结果表明，合理范围内分别提高各项判据阈值大小，会使列车滑行下的制动距离先降后升，压缩空气消耗量逐渐减小。

Abstract: Taking the train single wheel pair system as an example, a set of reasonable wheel-rail adhesion models was designed. Based on the braking distance and air consumption indexes, the slippage detection criteria of slippers were studied under low-adhesion rail surface and emergency braking conditions. The impact on the anti-skid performance of trains includes the deceleration criterion, speed difference criterion and slip rate criterion in coasting detection. The research results show that increasing the thresholds of each criterion within a reasonable range will cause the braking distance of the train to coast down and then increase, and the compressed air consumption will gradually decrease.

1. 引言

轨道车辆制动力的根本来源是轮轨蠕滑产生的黏着力 [1]。黏着力不够的情况下，车轮极易出现滑行甚至抱死，使制动距离延长，严重时会擦伤车轮踏面与轨道表面，给列车运行和停车安全带来极大危险。防滑器能够有效地检测出即将滑行的车轮并采取措施遏制滑行趋势，恢复黏着，一定程度上能够缩短制动距离。近年来随着列车运行速度的不断提高，给制动的安全性和可靠性带来更高挑战，防滑性能亦是其中关键，而防滑器的内部控制参数对防滑性能影响尤其明显，如滑行检测判据参数，因此有必要通过仿真手段展开研究。

通常地，各大防滑器厂家和主机厂对防滑性能的评价往往取决于制动距离单一指标 [2]，它的大小反映了防滑器在制动防滑过程中对轮轨有效黏着利用的充分程度，制动距离愈短表明黏着利用愈充分，防滑性能愈优。实际上，防滑器进行滑行控制时需要不断调整滑行轴的制动缸压力，防滑阀过于频繁的充排气会大量消耗总风缸里的压缩空气，严重时若空压机来不及补风，将引起总风压力下降过多触发紧急制动，给列车停车安全带来更大的危险。因此笔者认为，对列车防滑性能的评价应同时兼顾制动距离与防滑过程耗风量两者影响。

本文通过Matlab/Simulink和AMEsim软件联合仿真，建立了单轮对制动防滑控制系统，从制动距离与耗风量两个指标出发，研究低黏着轨面、紧急制动工况下防滑器中不同减速度判据阈值β、速度差判据阈值∆v以及滑移率判据阈值λ对防滑性能的影响，并对仿真结果进行了分析。

2. 防滑器

滑行检测和滑行后的再黏着控制是防滑器的主要任务。滑行检测用于判断车轴是否出现滑行，这是进行防滑控制的前提。目前滑行检测判据主要有速度差、减速度、减速度微分和滑移率四种，最常用的是减速度判据和速度差判据 [3]。

性能优异的防滑器能够有效缩短滑行制动距离，并能避免消耗过多的压缩空气，本文中使用制动距离延长比和相对耗风量来表征防滑性能。制动距离延长比是评价防滑控制性能最主要的指标，它反映了防滑控制器在低黏着路面下对轮对滑行的控制能力以及对黏着利用的充分程度，表征了该防滑器的制动效率。而相对耗风量则反映了防滑器对风源的负载能力，防滑过程中需要不断对制动缸进行充、排气，若防滑阀动作过频繁，耗风量过高，对风源系统的负载也会急剧增大，空气消耗严重时甚至可能导致总风压力不足而无法对制动缸再充气，带来停车安全问题，耗风量表征了防滑器的经济性、安全性。

其中，制动距离延长比计算公式为：

$a=\frac{S_{低黏着}-S_{干轨}}{S_{干轨}}\text{*}100\text{\%}$ (1)

式中：

$S_{低黏着}$ 为低黏着滑行工况下的制动距离；

$S_{干轨}$ 为干轨不滑工况下的制动距离。

相对耗风量计算公式为：

$b=\frac{V_{低黏着}}{V_{干轨}}$ (2)

式中：

$V_{低黏着}$ 为低黏着滑行工况下的耗风量，单位为NL (标升)；

$V_{干轨}$ 为干轨不滑工况下的耗风量，单位为NL。

下面将建立单轮对防滑控制系统模型，结合制动距离延长比以及相对耗风量两项指标对防滑器的滑行检测判据开展仿真研究。

3. 单轮对防滑控制系统模型

不同于制动控制，列车的防滑控制为单轴控制，且防滑过程主要体现在轮对处。轮轨间黏着系数较低即黏着力不足使车轮转速与平移速度出现较大速度差，导致轮轨关系进一步恶化，最终出现车轮抱死滑行情况。故通过仿真手段研究制动防滑时，可基于单轮对建立防滑控制系统以简化模型，节约建模时间成本，并可避免由于车辆结构参数如一系悬挂、二系悬挂刚度、阻尼等设置不当带来的模型失准问题，提高建模精度。本研究建立的单轮对防滑控制系统模型框架如图1所示。

制动过程中，制动缸压力升高，基础制动装置向单轮对施加制动力矩 $M_{brake}$ ，若轮轨之间的黏着力 不足，轮对转速ω下降较快，开始滑行，防滑器接收轮对的平动速度 与转动速度 ，根据内部滑行检测逻辑与控制策略，输出HV、RV信号控制防滑阀动作调节制动缸压力，从而控制轮对滑行。本文Matlab/Simulink及AMesim模型在建立过程中参考了同济大学左建勇、刁峰的论文 [4] [5]，此处对模型建立方法和仿真的有效性验证不再赘述。

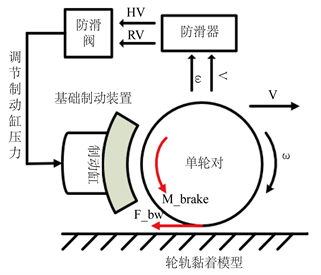
Figure 1. Single wheel pair anti-skid control system model frame

图1. 单轮对防滑控制系统模型框架

对本文研究内容而言，轮轨黏着模型的准确度较为重要，由于缺乏实际试验数据，本文选取了1999年Oldrich Polach提出的黏着力计算模型作为仿真模型，该模型能够反映黏着系数与轴重、车速、滑移率的关系，并且适用于滑动区域不稳定工况下即滑行工况下黏着系数的计算，无论是求解效率还是求解精度都有一定的保证，计算方式见下式3。该模型包含5个设置参数，K_a为黏着区衰减因子，K_s为滑动区衰减因子， ${\mu }_0$ 为轮轨最大摩擦系数，A为轮轨间极限滑动速度下摩擦系数与最大摩擦性因素的比值，B为摩擦系数调节参数，通过调节以上几个参数值获取不同工况下的黏着模型，表1描述了3中不同工况下的黏着模型参数取值。

$\mu =\frac{2f_0\left[\left(1-A\right)e^{-Bw}+A\right]}{\text{π}}\left[\frac{\frac{2C\text{π}{a}^{2}b}{3Q\mu }s}{1+\left(\frac{2C\text{π}{a}^{2}b}{3Q\mu }s\right)}+\arctan \left(\frac{2C\text{π}{a}^{2}b}{3Q\mu }s\right)\right]$ (3)

式中：

$\mu$ 为黏着系数；

$f_0$ 为轮轨最大摩擦系数；

Q为轴重；

A，B为摩擦系数调节参数；

$w$ 为相对滑动速度即 $V-\omega \cdot r$ ；

a为轮轨椭圆接触区纵半轴长度；

b为轮轨椭圆接触区横半轴长度；

C为轮轨接触剪切刚度；

s为滑移率。

Table 1. Parameters of wheel/rail adhesion calculation model

表1. 轮轨黏着力计算模型参数取值

通过黏着模型计算公式，结合上述模型参数，绘制低黏着工况下黏着系数与速度、滑移率的三维曲面，如图2所示，可以看到，黏着系数与滑移率的关系呈现为先增大后减小的规律，而黏着系数与速度的关系则是随速度的增大，黏着系数逐渐降低；此外不同速度下黏着系数峰值点对应的滑移率在5%~20%之间，这与国际铁路联盟(UIC)研究试验局(ORE)测得的轮轨黏着规律基本一致，根据该试验局大量的试验数据和分析得知，轮对发生滑行时，粘着力随着蠕滑率增大而增加，黏着力在某一点达到最大值时的蠕滑率约为5%~20%，当蠕滑率继续增大时粘着力下降，轮轨黏着与轮轨蠕滑率曲线关系如图3所示 [6]。由此可见，此组黏着模型比较接近低黏着轨面真实情况，将在此低黏着模型下开展防滑控制参数的研究。

Figure 2. Three-dimensional surface of adhesion coefficient, vehicle speed and slip rate under low adhesion conditions

图2. 低黏着工况下的黏着系数与车速、滑移率三维曲面

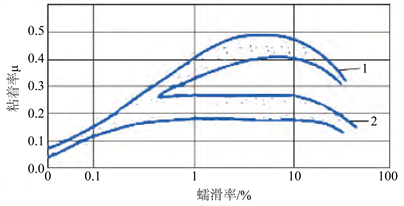1——在干燥的钢轨上；2——在潮湿的钢轨上。

Figure 3. Relationship between wheel-rail adhesion and slip ratio measured by ORE

图3. ORE测得的轮轨黏着与滑移率曲线关系

4. 滑行检测判据对防滑性能的影响规律仿真研究

考虑到实际列车进行防滑控制时，从轴速信号的采集、传输到防滑控制器内部计算处理，最后到防滑阀收到控制指令开始动作这一过程有一定的延迟，通常在100 ms~200 ms之间，同样地在模型里加入150 ms的延时，以使仿真试验结果具有更高的真实性。下述将在制动初速为200 km/h，制动级位为紧急制动(a = 0.99 m/s²)下进行滑行检测判据对防滑性能影响规律仿真研究，表2为干轨工况下的仿真结果。

Table 2. Simulation results under dry rail conditions

表2. 干轨工况下仿真结果

4.1. 减速度判据

减速度判据是根据轮对本身转动速度下降的快慢，即减速度的大小来判断是否滑行。现有微机式防滑器中，此判据的阈值通常设定为3~4 m/s²。仿真研究中选取的减速度判据阈值和试验结果见表3，将仿真结果可视化成图4。

Table 3. Deceleration criterion simulation results

表3. 减速度判据仿真结果

Figure 4. Deceleration criterion simulation results

图4. 减速度判据仿真

可以看到，减速度判据阈值从3 m/s²依次增大至5 m/s²时，制动距离延长比会先下降后上升，但整体变化幅度不大，阈值设为4 m/s²时制动距离达到最小值，而相对耗风量则近似成比例线性下降。

由于本轮轨黏着模型为一确定模型，可绘制各减速度判据阈值在不同速度下的实际利用黏着曲线，见图5。图中各实际利用黏着曲线随着减速度判据阈值增大，轮对滑移率摆动的幅度加大(主要是防滑器检测到滑行时对应的轮对滑移率向右侧移动)，由此引起防滑控制过程中轮轨实际利用黏着的变化，但这种变化对于制动距离的影响较为微小，因此制动距离延长比相差不大。而相对耗风量逐渐下降是由于减速度判据阈值提高，使得防滑器检测轮对的灵敏度下降，防滑控制的频率降低，制动缸压力调整次数减少，因此耗风量依次递减。综合制动距离延长比与相对耗风量来看，减速度判据阈值设为4~4.5 m/s²较为合适。

4.2. 速度差判据

速度差判据是利用车轴轴速与基准轴速度差的大小即∆v来判断该轴是否出现滑行，在本仿真模型中对应轮对的转动速度ω与平动速度v的差值。仿真研究中选取的速度差判据阈值和试验结果见表4，将仿真结果可视化成图6。

(1) 减速度判据β = 3 m/s² (2) 减速度判据β = 3.5 m/s² (3) 减速度判据β = 4 m/s² (4) 减速度判据β = 4.5 m/s² (5) 减速度判据β = 5 m/s²

Figure 5. The actual use adhesion curve under different deceleration criteria

图5. 不同减速度判据下的实际利用黏着曲线图

由图可知，改变速度差判据阈值 ，制动距离延长比变化明显，总体呈现出先减小后增加的趋势，在2 m/s时制动距离最短；耗风量同样随速度差判据阈值增大逐渐减少，阈值超过2 m/s后，减少幅度变缓。

图7反映了不同速度差判据下的实际利用黏着情况，当速度差判据为2~3 m/s时，实际利用黏着曲线恰好在最大可用黏着曲线附近摆动，且幅度较小，故黏着利用较高，制动距离短。而判据不超过2 m/s时实际利用黏着曲线偏离最大可用黏着，超过3 m/s时实际利用黏着曲线摆动幅度过大，两者均未充分利用轮轨黏着，使得制动距离延长。耗风量则同样是由于判据的增加使得滑行检测的灵敏度下降，因此防滑阀充排气次数下降。整体而言，速度差判据阈值设为2~3 m/s会获得较好的防滑性能。

Table 4. Speed difference criterion simulation

表4. 速度差判据仿真结果

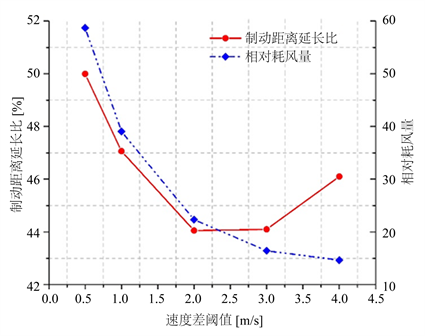
Figure 6. Speed difference criterion simulation

图6. 速度差判据仿真

(1) 速度差判据∆v = 0.5 m/s (2) 速度差判据∆v = 1 m/s (3) 速度差判据∆v = 2 m/s (4) 速度差判据∆v = 3 m/s (5) 速度差判据∆v = 5 m/s

Figure 7. The actual use adhesion curve under different speed difference criteria

图7. 不同速度差判据下的实际利用黏着曲线图

4.3. 滑移率判据

滑移率判据是通过车轮与轨道接触点的滑移率 的大小对轮对滑行情况进行检测判断，由车速与轴速的差值除以车速得到。仿真研究中选取的速度差判据阈值和试验结果见表5，将仿真结果可视化成图8。

Table 5. Slip rate criterion simulation results

表5. 滑移率判据仿真结果

与减速度和速度差判据影响规律一样，滑移率判据阈值从3%增加至12%，制动距离延长比同样为先降后升，相对耗风量逐步减少。阈值设为7%时，防滑后的制动距离最短。

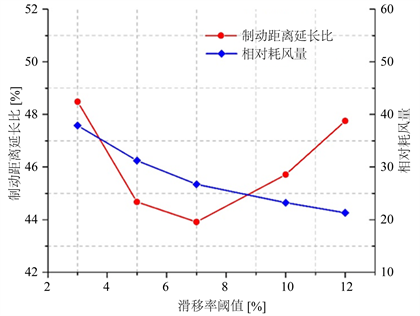
Figure 8. Slip rate criterion simulation

图8. 滑移率判据仿真

图9结果显示，滑移率判据低于5%时，实际利用黏着曲线偏离最大可用黏着曲线，黏着利用较低；超过10%后，防滑过程中轮对滑移率调整幅度增加，实际利用黏着曲线摆动范围变大，整体黏着下降，但是减少了压缩空气的消耗量。故滑移率判据阈值设置在7%左右，防滑性能较优。

(1) 滑移率判据λ = 3% (2) 滑移率判据λ = 5% (3) 滑移率判据λ = 7% (4) 滑移率判据λ = 10% (5) 滑移率判据λ = 12%

Figure 9. The actual use adhesion curve under different slip rate criteria

图9. 不同滑移率判据下的实际利用黏着曲线图

5. 结束语

基于单轮对防滑控制系统模型，结合制动距离延长比和相对耗风量两项有关防滑性能参数，研究了防滑器滑行检测判据对防滑性能的影响规律。

研究结果表明，在一定范围内改变减速度、速度差、滑移率判据阈值，会影响滑行轴在防滑过程中的滑移率变化区间以及防滑控制次数，进而影响实际轮轨黏着的利用，导致制动距离和耗风量发生变化。三者对防滑性能的影响规律基本一致，均呈现为判据阈值增大，制动距离先缩短后延长，耗风量逐步降低这一规律。与速度差、滑移率两个判据相比，改变减速度判据对于制动距离的影响程度较小。总体而言，减速度判据阈值设为4~4.5 m/s²，速度差判据阈值设为2~3 m/s，滑移率判据阈值设为7%左右，防滑性能较为优异。

目前使用的轮轨黏着模型为Polach数值模型，有待开展真实轮轨黏着情况的深入探索，以使本仿真研究结果更加准确。

参考文献