1. 引言
1713年,瑞士数学家Jocob Bernoulli引进了Bernoulli数的概念,用以解决Leibniz关于自然数的幂和问题 [1]。他证明了
这里Bernoulli多项式
由生成函数
所定义,而数
称为Bernoulli数(见文献 [1] 定理2)。1874年,德国数论学家E. Kummer利用Bernoulli数给出了非正则素数的定义,并用以解决代数数论中关于分圆域的类数和素数幂次Fermat方程的解的问题(见文献 [2])。
1755年,L. Euler为计算交错幂和引入了Euler多项式的定义。他证明了
这里Euler多项式
由生成函数
所定义(见文献 [1] 定理2)。1852年,德国数学家Scherk在著作中首次明确了Euler数和Euler多项式
的称谓 [3]。按照他的叫法,故
被称为Euler数。
1852年,为了研究对称群
中置换的组合性质,意大利数学家Angelo Genocchi给出了Genocchi数
的定义:
而k阶Genocchi多项式
定义为:
(1)
当
时,
为k阶Genocchi数,当
时,
为Genocchi多项式 [4]。
2019年,类比Kummer在1874年的工作,胡甦老师,Min-Soo Kim,沙敏老师以及德国学者Pieter Moree在文 [5] 中给出了Genocchi数对应的非正则多项式的定义,并得到了它们与分圆域类数之间的联系。
从数学分析我们知道
(见文献 [6] 的第74页)。类比Bernoulli数的定义,美国著名数论学家L. Carlitz [7] 在1956年提出退化的Bernoulli数的定义:
(2)
并得到了相应的Staudt-Clausen定理,见文献 [8]。
1999年,日本数论学家Arakawa和Kaneko [9] 通过Mellin变换给出了一类新的zeta函数
的定义:
其中
为k阶超对数(polylogarithm)函数。他们发现上面所定义的zeta函数
在负整
数处的特殊值通过poly-Bernoulli多项式加以表达,即
这里poly-Bernoulli多项式定义为:
(3)
并且
称为poly-Bernoulli数。
2015年,韩国特殊函数方向的专家T. Kim研究了一类退化的zeta函数并发现它在复平面上是解析的,并且在负整数处的特殊值即为Carlitz的退化Euler多项式 [10]。随后,他又在2016年推导出退化q-Bernoulli多项式的系列性质 [11] [12]。与此同时,他与俄罗斯学者D. V. Dolgy合作,用p-进~q-积分得出了退化q-Euler多项式的对称性 [13]。之后,他与D. S. Kim等学者合作对退化的Frobenius-Euler数和退化的poly-Bernoulli数,poly-Bernoulli多项式进行了研究,将若干经典的性质推广到了退化情形 [14] [15]。另外,他们还给出了完全退化的poly-Bernoulli多项式的定义:
(4)
并对其性质进行了详细证明 [16]。
受经典Genocchi多项式的定义(1),退化的Bernoulli数的定义(2),poly-Bernoulli多项式的定义(3)以及完全退化的poly-Bernoulli多项式的定义(4)的启发,我们通过下面的生成函数给出退化的Genocchi多项式
的定义:
(5)
当
时,
被称为退化的Genocchi数。注意到,
故
。我们也通过下面的生成函数给出poly-Genocchi多项式的定义:
(6)
当
时,
是poly-Genocchi数。当
时,有
,这是因为
我们还通过下面的生成函数给出完全退化的poly-Genocchi多项式的定义:
(7)
当
时,
被称为完全退化的poly-Genocchi数。注意到,
故
。
本文沿着前人的道路研究了上面定义的完全退化的poly-Genocchi多项式
的性质,并得到了
关于它们的下面五个组合恒等式。
定理1 下面等式成立:
特别地,
定理2 记
,有
定理3 记
,有
定理4 记
,有
定理5 记
,有
2. 预备知识
2.1. Stirling序列的定义 [5]
第一类Stirling数
通过下降阶乘
的展开式中x的幂的系数定义:
第二类Stirling数
则被定义为:
这里,当
时,下降阶乘
,
定义为1。
2.2. 退化的概念 [5]
对
,退化的指数函数
定义为:
其中
是退化的下降阶乘,当
,
。
当
时,
注意到,
。
2.3. 退化的Stirling数,Euler多项式,Bernoulli多项式 [5]
对
,退化的第二类Stirling数
定义为:
注意到,
。
对
,退化的Euler多项式
由如下的生成函数给出:
当
称为退化的Euler数。注意到,
所以有
。
对
,退化的Bernoulli多项式
由如下生成函数给出:
当
称为退化的Bernoulli数。注意到,
所以有
。
2.4. 完全退化的Poly-Bernoulli多项式 [14]
设
,完全退化的poly-Bernoulli多项式
的生成函数如下:
当
称为完全退化的poly-Bernoulli数。注意到,
所以有
。
3. 关于完全退化的Poly-Genocchi数和多项式的组合恒等式
我们需要下面的引理。
引理 对退化的Genocchi多项式
,我们有
(1)
,
(2)
。
证明 (1) 根据退化的Genocchi多项式 的定义(5),当x分别取1和0时有
的定义(5),当x分别取1和0时有
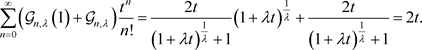
(2) 根据退化的Genocchi多项式 的定义(5)有
的定义(5)有

这里 是第一类Stirling数。 □
是第一类Stirling数。 □
定理1 下面等式成立:
 (8)
(8)
特别地,
 (9)
(9)
定理1的证明 根据完全退化的poly-Genocchi多项式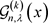 的定义(7)有
的定义(7)有
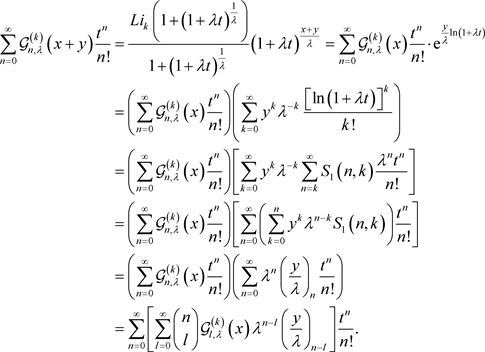
这里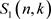 是第一类Stirling数,比较上式两端关于项
是第一类Stirling数,比较上式两端关于项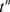 的系数,得到
的系数,得到

特别地,当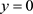 时,有
时,有

比较上式两端关于项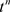 的系数即得定理的结论。 □
的系数即得定理的结论。 □
定理2 记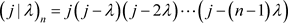 ,有
,有
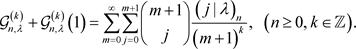 (10)
(10)
定理2的证明 根据完全退化的poly-Genocchi多项式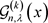 的定义(7)有
的定义(7)有

比较上式两端关于项 的系数即得定理的结论。 □
的系数即得定理的结论。 □
定理3 记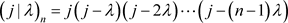 ,有
,有
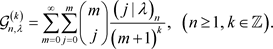 (11)
(11)
定理3的证明 根据完全退化的poly-Genocchi多项式 的定义(7)有
的定义(7)有
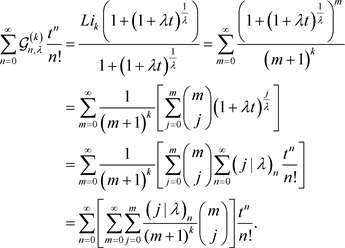
比较上式两端关于项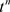 的系数即得定理的结论。 □
的系数即得定理的结论。 □
定理4 记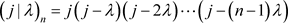 ,有
,有
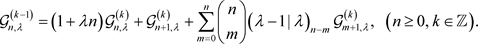 (12)
(12)
定理4的证明 根据完全退化的poly-Genocchi多项式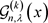 的定义(7)有
的定义(7)有
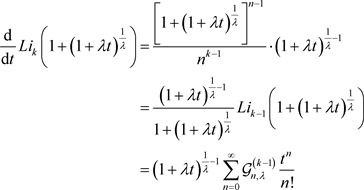 (13)
(13)
和
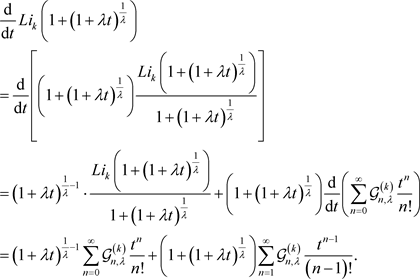 (14)
(14)
比较等式(13),(14)得到
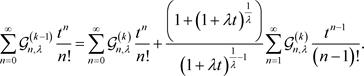
进一步化简得:
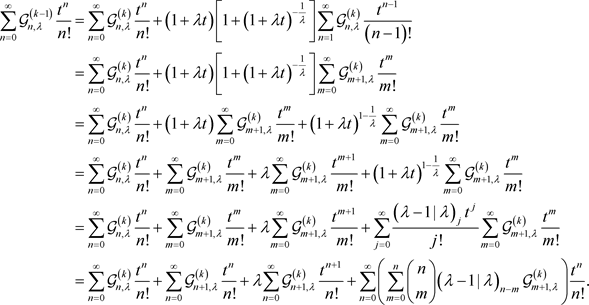
比较上式两端关于项 的系数,得到
的系数,得到
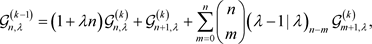
此即得定理的结论。 □
定理5 记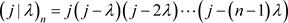 ,有
,有
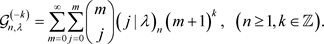 (15)
(15)
定理5的证明 根据完全退化的poly-Genocchi多项式 的定义(7)有
的定义(7)有

于是

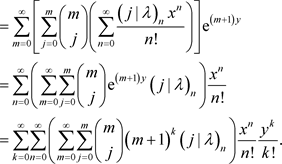
比较上式两端关于项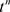 的系数即得定理的结论。 □
的系数即得定理的结论。 □