1. 引言
1960年,波兰数学家Opial [1] 证明了下面不等式
, (1)
其中
为区间
上的绝对连续函数,且
。由于其在微分方程、差分方程初边值问题研究中的重要性,许多学者给出了Opial不等式的各种推广及离散化的Opial不等式 [2] [3] [4],其中,Yang [5] 简化了(1)式的证明,并给出了推广的不等式
,
其中
、连续且满足
,
且为
上的有界非增函数;同时,Yang [5] 还给出了更一般的不等式
, (2)
其中
。关于离散形式的Opial不等式,Lasota [6] 也讨论了不等式
,
并给出了证明,其中
为一实数列满足
。
1988年,德国学者S. Hilger为了统一连续、离散情形的研究,在其博士论文中提出了时标的概念。此后,时标理论得到了快速发展,特别是M. Bohner和A. Peterson在文献 [7] [8] 中,系统分析了时标上一类非常重要的动力方程:时标上的动力方程。时标上的动力方程(系统)不仅可以统一连续和离散这两种特殊的情形,而且在其他学科中也有巨大的应用潜力,如量子力学等,是一个比较新的有着广泛应用前景的应用数学分支,其理论研究主要集中在边值问题、振动性、稳定性等方面。关于时标上的不等式研究,也有相关结果 [9] - [14]。
本文将研究Opial型不等式(2)在时标上的推广,其中在第二部分对时标的基本概念及基本理论作简要介绍,在第三部分中给出主要结果及其证明。
2. 预备知识
实数集
的任一非空闭子集称为时标,记为T。设时标T上的拓扑由
上的标准拓扑诱导,则有
下列定义:
定义1 [7]:设T为时标,对任意
,定义
,称
为前跳算子;
,称
为后跳算子。
在上面的定义中,称
(即如果t为时标T的最大值,则有
),而
(即如果t为时标T的最小值,则有
),其中
表示空集。
设
且
,若
,称点t是右发散(右稠密)的;若
,称点t是左发散(右稠密)的。既右发散又左发散的点称为孤立点,既右稠密又左稠密的点称为稠密点。
如果T的左发散点有最大值
,则定义
,否则
。
时标T上的区间
定义为
。
定义2 [7]:定义前跳graininess函数
为
,对任意的
。
设
为时标T上的一实函数,则
定义为
,即
为
的复合;同理,
定义为
,即
。
对于时标T上的实函数f,下面给出f在点
时的
导数(Hilger导数)的定义。
定义3 [7]:若对任意的
,存在t的邻域U,使得对任意
,都有
成立,则称
为f在t的
导数(Hilger导数)。
关于
导数,下列性质成立。
引理1 [8]:设函数
在
处可微,则有:
1) 若
存在,则
;
2)
;
3)
;
4) 若
,则
。
定义4 [7]:函数
称为右稠连续的,如果f在T的右稠密点出连续,在左稠密点出左极限存在。
记T上的右稠连续函数为
。
定义5 [7]:对任意的
,若满足
,则称函数
为f的一个原函数,且定义
积分为
,
。
关于
积分,有下面引理。
引理2 [8]:若
,
,
,则有
1)
;
2)
;
3)
;
4) 若
,
,则
;
5)
。
在后面的证明中,主要用到下面的时标上的Cauchy-Schwarz不等式。
引理3 [8]:设
,
,且满足
,则对函数
,有
成立。
3. 主要结果及证明
下面给出主要定理。
定理1:设T为任一时标,
,
为
上的右稠连续函数,且满足
,则
,
。 (3)
证明:对任意的
,定义
,则有
。由于
,
对上式运用指标分别为
和q的Cauchy-Schwarz不等式,可以得到
。
注意到
是单调递增的,利用其单调性,
,
。设
,根据链式法则,有
,
注意到
,
。
对上式两边同时进行积分,并由
,得
,
由此可得
,
故(3)式得证。
定理2:设T为任一时标,
,,
为
上的右稠连续函数,且满足
,则
,
。 (4)
证明:对任意的
,定义
,易知
非减且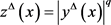 。由于
。由于
,
对上式运用指标分别为
和q的Cauchy-Schwarz不等式,可以得到
。
进一步可得
。
由于
,
,
注意到
为非减函数,可得
。 (5)
由(5)式,可计算得
,
故(4)式得证。
定理3:设T为任一时标,
,且
,
为
上的右稠连续函数,且满足
,则
,
。(6)
证明:因为
。 (7)
令
,分别运用定理1、定理2结论可知,
,
,
将上面两不等式代入(5)式可得(6),定理得证。
基金项目
国家级大学生创新创业训练项目(201811306045),池州学院教学团队(2018XJXTD03)。
NOTES
*通讯作者。