1. 引言
基于欠定线性方程组
,这里
,
,A是
的矩阵,b是已知的,x是未知的,本文只考虑非负解
的部分。寻找欠定线性方程组的稀疏非负解,就是求解如下的优化问题:
(1)
其中
指向量x中非零分量的个数。这类问题在信号处理,图像恢复和多光谱数据处理等领域引起了广泛的研究 [1] [2] [3]。
在现有的研究成果中,主要用贪婪法和松弛法来解决问题(1)。贪婪法主要包括正交匹配追踪算法 [4],正则化正交匹配追踪算法 [5] 以及压缩采样匹配追踪 [6] 和子空间追踪 [7]。这种类型的算法由于其相对较快的计算速度,而在实践中得到了广泛的应用。然而,当信号不是很稀疏或观测噪声水平较高时,贪婪法的性能无法得到保证。
松弛法是通过用一定的非负连续函数代替
范数,将
极小化模型转化为更易于处理的模型。常用于逼近
极小化模型的是
极小化模型。
极小化是一个凸优化问题,在矩阵A满足适当的条件下,
极小化可以精确地恢复稀疏信号。因此,
极小化被认为是解决稀疏性问题的非常有用的工具并得到了广泛的运用。此外,一些非凸函数
范数被提出作为
范数的松弛。与
极小化方法相比,非凸松弛模型通常具有更好的稀疏性,但通常较难求解。
求解约束优化问题(1)主要有两种算法。第一种算法是迭代重加权算法,其中两个最重要的迭代重加权算法是重加权
极小化 [8] 和迭代重加权最小二乘算法 [9]。另一种方法通常称为正则化方法,它通过引入正则化参数将问题(1)转化为下面的优化问题:
(2)
其中
,且
是给定的正则化参数。
本文的其他内容如下:首先给出一些符号定义和关于问题(2)的一阶优化条件。基于Cheng和Chen [10] 的研究,我们在加入非负约束
后,重新定义了四种关于问题(2)的稳定点:基本稳定点,强基本稳定点,L-稳定点,严格L-稳定点,并说明了它们之间的关系。随之提出了有效集方法求解问题(2),这种方法能够精准地找出L-稳定点邻域内的值为零的分量。接着提出了有效集Barzilar-Borwein算法求解问题(2)。最后进行了数据实验,证明了该算法可以有效的求解欠定线性方程组的稀疏非负解。
2. 符号说明
在本节中,我们将定义一些符号说明。假设
是问题(2)的最优解,我们定义有效集
是
中零分量的下标集合,无效集
是
中非零分量的下标集合:
定义2.1 [11] 令
,
,若向量值函数
满足
则称
为硬阈值算子。
注2.1 硬阈值算子是
极小化问题的最优解,即
在最近的研究中,Beck和Hallak [12] 提出了下面问题的一些基本定义
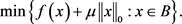 (3)
(3)
其中
,
。
定义2.2 (基本稳定点)如果
,则有:
(4)
其中
表示
在第i个分量的梯度。那我们称满足条件(4)的
为问题(2)的基本稳定点。
定义2.3 (L-稳定点)向量
称作问题(3)的L-稳定点需满足:
其中
,
且
是集合B的指标函数,而指标函数也就是
当
时,问题 等价于问题 ,则上述条件等价于下面的条件:
向量
满足如下条件就称为问题(2)的严格L-稳定点:
(5)
向量
满足如下条件就称为问题(2)的强基本稳定点:
由上述条件不难得出由问题(2)的严格L-稳定点可以推出问题(2)的L-稳定点,强基本稳定点和基本稳定点。
对于函数
,称
是函数
在x处的下降方向,如果常数
,使得
我们用
表示函数
的所有下降方向的集合:
类似于文献 [10] 的定理2.1,下面的定理将给出集合
更精确的表达形式,这将有利于我们设计线性搜索方法解决问题(2)。
定理2.1 假设
,由于
是连续可微的,集合
可表示为:
3. 有效集估计
通常来说,有效集的效率很大程度上取决于如何找到最优点处的有效约束。接下来,将介绍有效集的估计并用它来逼近原问题的严格L-稳定点。我们用集合
逼近
,集合
逼近
:
和
下面的定理表明,当点
足够接近严格L-稳定点时,则上述有效集的逼近集合
是集合
的子集。
定理3.1 假设
是问题(2)的严格L-稳定点,序列
收敛于
,则对于足够大的k有:
证明:假设
是问题(2)的严格L-稳定点,如果
,由于
所以结论成立。假设
,对于任意的
,由(5)可知:
因为
是连续的,故有:
因此,
也就是
。
另一方面,对于任意的
,有
由于序列
收敛于
,可得:
对于足够大的k,可得
。再由最优性条件,我们有
。因此,
也就是
,证毕。
下面的定理表明,当
是问题(2)的严格L-稳定点时,我们可以得到集合
。
定理3.2 假设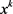 是问题的严格L-稳定点,则有:
是问题的严格L-稳定点,则有:
证明:假设
是问题的严格L-稳定点,对于任意的
,由条件(5)可得
。而对于任意的
,我们有
。但事实上,如果存在
,由条件(5)可得
且有:
由此可得
,故
。同理可得
,证毕。
4. 有效集算法
在本节中,首先给出搜索方向的定义和一些相关性质,然后介绍一种有效集Barzilar-Borwein算法来求解问题(2),并分析了该算法的全局收敛性。
4.1. 搜索方向的一些性质
令
是第k个迭代点,为了简化表述,令
为了定义搜索方向,进一步将
分成两个部分:
搜索方向
,定义
为:
(6)
其中
是Barzilar-Borwein算法的步长,其精确的定义将在4.2节中给出。集合
表示零分量的下标集合,且包含满足条件(5)的变量的下标集合。集合
包含不满足条件(5)的变量的下标集合。因此,给出定义:
(7)
(8)
下面的定理表明
当且仅当
是问题(2)的一个严格L-稳定点。
定理4.1 假设
由上述定义式(6)~(8)所表示。
当且仅当
是问题(2)的一个严格L-稳定点。
证明:令
,由
的定义和搜索方向
,可得
。如果
,由
的定义和
可得:
如果
,由
的定义可知:
反过来,假设
是问题(2)的严格L-稳定点。如果
,我们称
,
且
。事实上,如果
,由式(5)可得:
这与假设条件矛盾。因此,对
有:
证毕。
定理4.2 假设
且
,其中
由式(6)~(8)所表示,则
是问题(2)的一个L-稳定点。
证明:对于
,当
时,由于
,可得
。再由
的定义,我们可得:
对于
,由
,可得:
对于
,由于
的连续性和
,有
证毕。
下面的定理表明,如果
是问题(2)的强基本稳定点,由(6)~(8)定义的
是f在
处的下降方向。
定理4.3 假设
由(6)~(8)式定义,可得
(9)
此外,等号成立当且仅当
是问题(2)的强基本稳定点。
证明:由
的定义可知:
再由
的定义可知:
对于任意的
,我们有:
综上所述,我们可以得到
。
假设
是问题(2)的强基本稳定点。对于任意的
,有
。由此,对于任意的
,有
,则有
。由
的定义可知
。对于任意的
,我们有
。相反地,假设不等式(9)的左边等于0,我们有:
由
的定义可知
。由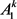 的定义可得:
的定义可得:
由此可知,
是问题 的强基本稳定点,证毕。
4.2. 算法
基于上述讨论和非单调线性搜索 [13],类似于文献 [10],我们提出了一种有效集Barzilar-Borwein算法来求解问题(2)。但不同于文献 [10] 的是我们在加入非负约束后,重新定义了有效集和有效集部分的搜索方向,产生了不同的迭代点,加快了算法的收敛速度。
算法4.1 (有效集Barzilar-Borwein算法,简记ABB算法)
步0 初始化
,取
,
且
,正整数M,取
。
步1 进行收敛性检验,如果满足停止条件,则用近似解
终止。
步2 计算
且
由式(6)~(8)确定。
步3 如果 ,满足不等式
,满足不等式
(10)
执行步5,否则执行步4。
步4 确定
满足不等式
(11)
其中
,
,执行步5。
步5 计算
,取
,返回步1。
接下来,将给出
的显性形式,运用了Barzilar-Borwein (BB)算法 [14] 的基本思想。类似于Barzilar-Borwein步的思想,通过求解下面的优化问题:
其中
且
,我们得到Barzilar-Borwein步长如下:
为了控制
的大小值,我们用区间
来限制,其中
是给定的正常数。因此,我们设
(12)
为了简单起见,我们将步长(12)代入式(6),简化了算法4.1。
4.3. 全局收敛性分析
下面将分析算法4.1的全局收敛性。类似于文献 [13] 中的分析,可以得到了如下的引理。
引理4.1 假设序列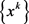 是由算法4.1产生。如果存在一个正整数
,对于所有
,满足线性搜索(11),我们有:
是由算法4.1产生。如果存在一个正整数
,对于所有
,满足线性搜索(11),我们有:
(13)
下面的定理和定理4.2表明序列
的任意聚点都是问题(2)的L-稳定点和强基本稳定点。
定理4.4 假设序列
是由算法4.1产生。如果对于所有的k都有
,则序列
的任意聚点
都是问题(2)的L-稳定点或强基本稳定点。
证明:假设对于所有的k都有
,且
为序列
的任意聚点。则存在一个无限指标集合K,满足
使得:
考虑到不同集合
的数量是有限的,对于任意的
,我们考虑两种情况。情形(1):如果存在一个无限指标集合
,对于所有的
,线搜索(11)都满足。通过对不等式(10)求和,可得
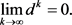
则由定理4.2可知结论成立。情形(2):如果存在一个正整数
,对于所有的
,线搜索(11)都满
足。如果序列
有一个非零的极限值,我们由(13)式可知
则由定理4.2可得知结论成立。否则,如果我们有
,对于所有的
,由线搜索(11)规则可得
(14)
另一方面,对于充分大的
,由中值定理可得
其中
。将上述等式带入(14),可得
由于序列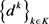 是有界的,不失一般性地,存在
使得
,结合引理4.1可知,
。再由最后一个不等式取极限得
。由定理4.3得出矛盾,故结论成立,证毕。
是有界的,不失一般性地,存在
使得
,结合引理4.1可知,
。再由最后一个不等式取极限得
。由定理4.3得出矛盾,故结论成立,证毕。
5. 数值实验
下面将进行一些数值实验来验证算法4.1对于求解欠定线性方程组的稀疏非负解是有效的。所有的实验结果都是在联想笔记本电脑(2.50 GHz, 8.00 GB of RAM)上实现的,数学软件采用MATLAB R2016a。
基于文献 [15] 的实验证实了
优化问题可连续的有效性,我们将算法中嵌入连续化过程。具体方法就是在考虑求解问题(2)前,先求解如下一系列问题
其中
且N是一个正整数。我们用问题的解
作为下一个问题的初始迭代点。取
,
,区间
经过取对数化处理后,再将其分成N个均匀分布的子区间。我们选择序列
作为子区间的端点,并对
做了一个处理,即令
。算法中涉及的参数设计如下:
。首先用标准高斯分布的独立样本填充
的度量矩阵A,并且对这些行进行正交化。而真实解
是一个具有有效集
的T-稀疏信号,观测向量b定义为:
其中e是根据均值为零且方差为10-2的高斯分布绘制的。
在实验中,我们研究了参数N和L对算法的影响,设
和
,
,并考虑了稀疏度的范围:
的非零分量的数量T在1到60都是可行的。算法的初始点是零向量,当满足
或
条件时,停止运算。下面将从平均迭代步数(Iter)、平均误差(
)和运算时间(Time)三个方面来对ABB算法的性能进行评估。

Table 1. n = 5 × 10 3 , L = 1 / 5 , the results of ABB algorithm to solve the problem
表1. n = 5 × 10 3 , L = 1 / 5 时ABB算法求解问题的计算结果


Table 2. n = 5 × 10 3 , L = 1 / 4 , the results of ABB algorithm to solve the problem
表2.
时ABB算法求解问题的计算结果

Table 3. n = 5 × 10 3 , L = 1 / 2 , the results of ABB algorithm to solve the problem
表3.
时ABB算法求解问题的计算结果

Table 4. n = 5 × 10 3 , L = 1 , the results of ABB algorithm to solve the problem
表4.
时ABB算法求解问题的计算结果
由上述表1~4可以看出,当问题的规模取
时,
,ABB算法产生了较大的平均误差。在
时,ABB算法产生的平均误差较小。而L的取值变化对于ABB算法产生的平均误差影响很小。
对于上述表格中计算的数据,我们将绘图分析在
时,L和N的取值变化对于ABB算法求解问题的平均迭代次数和运算时间产生的影响。
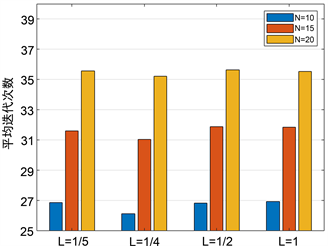
Figure 1. The influence of the change of N value on the average number of iterations at different L levels
图1. 不同L水平下,N取值变化对平均迭代次数的影响
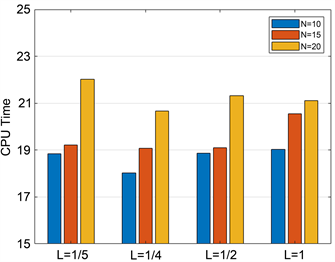
Figure 2. The influence of the change of N value on operation time at different L levels
图2. 不同L水平下,N取值变化对运算时间的影响

Figure 3. The influence of the change of L value on the average number of iterations at different N levels
图3. 不同N水平下,L取值变化对平均迭代次数的影响
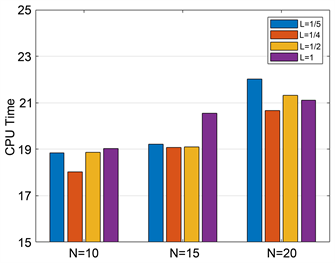
Figure 4. The influence of the change of L value on operation time at different N levels
图4. 不同N水平下,L取值变化对运算时间的影响
由图1和图2可以明显看出,当L的值一定时,随着N的取值变大,迭代步数和运算时间都会增加。同样的,由图3和图4可以明显看出,当N的取值一定时,可以看出
时,平均迭代步数和运算时间都是最小的。由此可知,当
时,可以得到最优的实验结果。

Table 5. n = 10 4 , L = 1 / 5 , the results of ABB algorithm to solve the problem
表5.
时ABB算法求解问题的计算结果

Table 6. n = 10 4 , L = 1 / 4 , the results of ABB algorithm to solve the problem
表6.
时ABB算法求解问题的计算结果

Table 7. n = 10 4 , L = 1 / 2 , the results of ABB algorithm to solve the problem
表7.
时ABB算法求解问题的计算结果

Table 8. n = 10 4 , L = 1 , the results of ABB algorithm to solve the problem
表8.
时ABB算法求解问题的计算结果
由表5~8中的结果可知,当问题规模达到
时,我们依旧可以得到相同的结论。当L的值一定时,随着N的取值变大,迭代步数和运算时间都会增加。当N的取值一定时,可以看出
时,平均迭代步数和运算时间都是最小的。由此可知,当
时,可以得到最优的实验结果。综上可知,ABB算法可以快速有效地求解欠定线性方程组的稀疏非负解。
6. 小结
本文主要讨论了求解欠定线性方程组的稀疏非负解问题。首先将线性约束条件惩罚到目标函数上,给出了
正则优化模型的严格L-稳定点定义。随之提出有效集方法识别严格L-稳定点邻域内的零分量,基于这种快速精准的识别技术,设计了有效集Barzilar-Borwein算法,并且证明了由该算法产生的序列的任意聚点都是强稳定点。最后进行了数据实验,证明了该算法可以快速有效地求解欠定线性方程组的稀疏非负解。
NOTES
*第一作者。
#通讯作者。