基于改进遗传算法的无人机搜索路径规划的研究

Research on UAV Search Path Planning Based on Improved Genetic Algorithm

摘要: 本文针对无人机搜索目标时移动速度的大小和方向不确定的问题，设计了基于改进遗传算法的搜索路径规划算法。传统的基于解析的办法适应性不强，不便于计算机自动化计算的实现。本文提出了基于改进遗传算法的搜索路径规划算法，将目标移动方向的概率时间等参数作为动态的人工势场综合考虑，提高了搜索路径规划问题求解算法的适应性，对于复杂的搜索区域和目标移动概率，均具有较高的适应性和自动化程度。根据遗传算法中适者生存的思想，择优选出更加优化的搜索路径。在这个过程中，将无人机的路径点当作生物的基因，把搜索路径看作是生物的染色体，然后通过杂交、选择、变异等操作得到更加优化的搜索路径。设置算例进行仿真计算，由仿真计算结果可知，本文提出的基于改进遗传算法的搜索路径规划算法是可行的，并且具有灵活性强、效率高和自动化的优点。

Abstract: Aiming at the problem of UAV searching for the target with uncertain moving speed and direction, this paper designs a search path planning algorithm based on improved genetic algorithm. The traditional method based on analysis has not strong adaptability and is not convenient for the realization of computer automatic calculation. In this paper, a search path planning algorithm based on improved genetic algorithm is proposed, which considers the probability time and other parameters of the target moving direction as a dynamic artificial potential field, improves the adaptability of the algorithm for solving the search path planning problem, and has a high degree of adaptability and automation for the complex search area and the target moving probability. According to the idea of survival of the fittest in genetic algorithm, a more optimal search path is selected. In this process, the path point of UAV is regarded as the gene of organism; the search path is regarded as the chromosome of organism; and then the search path is optimized through hybridization, selection, mutation and other operations. Then, an example is set up for simulation calculation. From the simulation results, we can see that the search path planning algorithm based on the improved genetic algorithm is feasible, and has the advantages of flexibility, efficiency and automation.

1. 引言

无人机搜索路径规划就是为执行搜索任务的无人机规划搜索路径，以能够尽早地发现被搜索的目标。无人机搜索路径是决定搜索任务成败的关键因素，无人机搜索路径规划是无人机搜索任务规划的核心和关键模型。

周延安，梅刚 [1] 提出的反辐射无人机的搜索路径规划，针对反辐射无人机，利用遗传算法的杂交、变异操作，得到满足反辐射无人机任务需求的搜索路径。候岳奇 [2] 等人针对未知环境下无人机群的搜索路径规划进行了研究。他们是在先验信息的基础上，建立覆盖分布地图，然后通过多个无人机形成的集群，以覆盖率作为搜索奖励，并以基于CDM计算得出的覆盖率作为衡量搜索效果的指标来进行的无人机集群的搜索路径规划。李松等人 [3] 提出了一种转换策略，将无人机搜索路径规划问题转换为车辆的路径规划问题，并且在充分考虑无人机执行搜索任务的实际情况后建立模型，通过求解混合整数线性问题得出最优的解，然后得到多无人机协同搜索的路径。多无人机协同区域搜索路径规划在 [4] [5] 中有较多的研究，他们分别是基于D-S证据理论和基于Voronoi图质心进行的路径规划，他们都是针对多无人机进行的，并且根据任务特性，制定相应的协同方式和策略，然后基于各自的算法得到搜索路径。

本文针对目标移动速度和方向均存在不确定性的情况，首先建立了目标分布概率模型和无人机探测模型以及搜索区域网格化模型，然后设计了基于改进遗传算法的搜索路径规划算法，并设置算例对算法进行了验证。

2. 目标分布概率模型

假设在时刻 $t_0$，目标的位置为 $\left(x_0,y_0\right)$，以速度v做直线运动，速度v在区间 $\left[v_{\min },v_{\max }\right]$ 内均匀分布。速度的方位角 $\theta$ 的概率分布已知，设为 $p\left(\theta \right)$。在 $t_0$ 时刻目标位于 $\left(x,y\right)$ 处的概率密度为 $f\left(x,y,t\right)$。

当 $x=vt\cos \theta$， $y=vt\sin \theta$ 时：

$f\left(x,y,t\right)=\frac{p\left(\theta \right)}{v_{\max }-v_{\min }}$ (2.1)

否则：

$f\left(x,y,t\right)=0$ (2.2)

3. 无人机探测模型建模

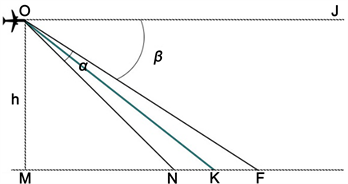
假设无人机的传感器对地面进行探测时形成的视场在地面的投影是一个等腰梯形，如图1所示。为了简化模型，本文将搜索区域方格化。

设无人机飞行高度为h、水平视角为λ (λ为图中的∠BOA)、垂直视角为α、俯视角为β，如图2所示。在AB边、PQ边和CD边上分别取它们的中点N、K、F，其中OK边是∠NOF的角平分线。网格的边长不能大于梯形的最长边CD，也不宜小于最短边AB，本文取梯形的中线PQ为网格的边长。

根据图中我们可得：

$MK=h/\tan \frac{\alpha }{2}$ (3.1)

$OK=h/\sin \frac{\alpha }{2}$ (3.2)

$PQ=20K\tan \frac{\lambda }{2}$, $S=P{Q}^2$ (3.3)

式中PQ是网格边长，S代表的是网格面积即视场面积。以网格边长为PQ，对搜索区域进行网格化，如图3所示。

x、y、z轴的单位是m，用来表示无人机飞行时的位置关系。

Figure 1. Ground projection diagram of UAV detection field of view

图1. 无人机探测视场地面投影示意图

x、y、z轴的单位是m。

Figure 2. View angle range diagram of UAV

图2. 无人机视角角度范围示意图

x、y轴的单位是km。下同。

Figure 3. Grid diagram

图3. 网格化示意图

4. 算法设计

4.1. 路径编码

无人机的搜索路径可以用无人机经过的网格序列来表示。每个网格又可以使用网格的中心坐标x，y来表示。因此，无人机的路径可以使用 $\left(x,y,t\right)$ 组成的序列来表示(t为无人机经过网格的时间)。

另外，网格还可以使用网格的索引 $g_i$ 来表示，则无人机的路径可以表示为 $\left(g_i,t\right)$ 的序列。

4.2. 交叉算子

假设有两条父路径分别为：

$p_1=\left[g_1,g_2,g_3,\cdots ,g_{k-1},g_k,g_{k+1},\cdots ,g_m\right]$

$p_2=\left[x_1,x_2,x_3,\cdots ,x_{k-1},x_k,x_{k+1},\cdots ,x_m\right]$

则对于随机生成的一个位置k，则交换后两个子代路径为：

$p_3=\left[g_1,g_2,g_3,\cdots ,g_{k-1},y_1,y_2,\cdots ,y_n,x_k,x_{k+1},\cdots ,x_m\right]$

$p_4=\left[x_1,x_2,x_3,\cdots ,x_{k-1},z_1,z_2,\cdots ,z_l,g_k,g_{k+1},\cdots ,g_m\right]$

其中， $y_1,y_2,\cdots ,y_n$ 为 $g_{k-1}$ 到 $x_k$ 之间直线连接经过的网格。 $z_1,z_2,\cdots ,z_l$ 为 $x_{k-1}$ 到 $g_k$ 之间直线连接经过的网格。由上可知，对于两个路径，在进行交叉操作后，路径的长度可能会发生变化，如图4所示。

Figure 4. Schematic diagram of cross operation

图4. 交叉操作示意图

4.3. 变异算子

变异包含在两个点之间插入一个点、在路径上删除一个点、在路径上删除一个点同时增加一个点这三种情况，图5为在路径上删除一个点之后再增加一个点的变异过程的示意图。

假设一个父路径：

$p_1=\left[g_1,g_2,g_3,\cdots ,g_{k-1},g_k,g_{k+1},\cdots ,g_m\right]$

则对于随机生成的某一个位置 $k-1$ 和k，发生变异得到的子代路径可以为：

$p_2=\left[g_1,g_2,g_3,\cdots ,g_{k-1},B_1,B_2,\cdots ,B_{n-1},B_n,B_{n+1},\cdots ,B_k,g_k,g_{k+1},\cdots ,g_m\right]$

$p_3=\left[g_1,g_2,g_3,\cdots ,g_{k-1},A_1,A_2,\cdots ,A_{n-1},A_n,g_{k+1},\cdots ,g_m\right]$

$p_4=\left[g_1,g_2,g_3,\cdots ,g_{k-1},C_1,C_2,\cdots ,C_{n-1},C_n,C_{n+1},\cdots ,C_k,g_{k+1},\cdots ,g_m\right]$

$B_n$ 为变异后在 $g_{k-1},g_k$ 两个点之间插入的点， $B_1,B_2,\cdots ,B_{n-1}$ 为 $g_{k-1}$ 到 $B_n$ 点之间直线连接经过的网格， $B_{n+1},\cdots ,B_k$ 为 $B_n$ 到 $g_k$ 之间直线连接时经过的网格。

$p_3$ 是删掉了点 $g_k$ 后得到的， $A_1,A_2,\cdots ,A_{n-1},A_n$ 是 $g_{k-1}$ 到 $g_{k+1}$ 之间直线连接时经过的网格。

$p_4$ 是在删掉了一个点 $g_k$ 同时增加了一个点 $C_n$ 后得到， $C_n$ 为变异后在 $g_{k-1},g_{k+1}$ 两个点之间插入的点， $C_1,C_2,\cdots ,C_{n-1}$ 为 $g_{k-1}$ 到 $C_n$ 点之间直线连接时经过的网格， $C_{n+1},\cdots ,C_k$ 为 $C_n$ 到 $g_{k+1}$ 之间直线连接时经过的网格。

Figure 5. Schematic diagram of mutation operation

图5. 变异操作示意图

4.4. 适应度函数

适应度函数，是评价路径优劣的重要指标。计算搜索路径的适应度，需要综合考虑影响搜索效果的诸多因素，并对这些因素进行量化、分配权重、综合、择优。

假设无人机的路径为方格序列，一条搜索路径是由 个搜索方格组成，搜索路径的方格序列表示为 $\left\{g_1,g_2,g_3,\cdots ,g_m\right\}$，适应度函数可以表示为：

$F={\displaystyle {\sum }_{i=1}^{m}f\left(x_i,y_i,t_i\right)}$ (4.1)

式中，F表示路径的适应度值， $\left(x_i,y_i,t_i\right)$ 代表第i个搜索方格的中心点坐标。

5. 算例

目标速度在20至30 km/h之间、初始位置为(0, 0)、初始速度方向为50˚ (以正东为0，逆时针方向旋转)。目标的航向分布概率如表1所示。

Table 1. Probability table of possible target heading distribution

表1. 目标可能的航向分布概率表

无人机的最大飞行速度为80 km/h、初始位置(2, 2)、最大航偏角为50˚、完成搜索任务的时间上限为 $t_g=60\min$。

设遗传算法进行时交叉概率 $p_c=0.6$ 、变异概率 $p_d=0.05$ 、增益系数 $k_m=2$ 、初始种群数量 $N=20$。

按照本文设计的基于改进遗传算法的搜索路径规划算法，基于上述的搜索背景和搜索相关的数据，进行搜索路径规划的仿真计算。

当目标的移动速度为一个固定的值的时候，由目标可能的航向分布概率表中的目标航向分布概率可以得到目标的概率分布密度函数计算公式：

$f\left(x,y,t\right)=\{\begin{array}{l}f\left(v\csc {\theta }_1,v\sin {\theta }_1,t\right)=\frac{1}{4}\\ f\left(vt\csc {\theta }_2,v\text{tin}{\theta }_2,t\right)=\frac{1}{4}\\ f\left(v\csc {\theta }_3,v\text{tin}{\theta }_3,t\right)=\frac{1}{4}\\ f\left(v\csc {\theta }_4,v\sin {\theta }_4,t\right)=\frac{1}{4}\end{array}$ (5.1)

当目标的移动速度是一个变化的值的时候：

$x_i=vt\cos \theta ,y_i=vt\sin \theta \left(i=1,2,3,\cdots ,m\right)$

$f\left(x,y,t\right)=\{\begin{array}{l}\frac{1}{8\Delta v}x\in x_i,y\in y_i\\ 0否则\end{array}$ (5.2)

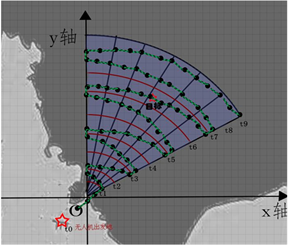
Figure 6. A schematic of the calculated UAV’s search path

图6. 计算得到的无人机搜索路径

在某次计算中，得到一条搜索路径如图6所示。得到的是一条弓形的搜索路径，和传统的“之”字行扫描方法得到的搜索路径有所区别，因为本文的搜索目标的移动速度存在一个速度区间，在第一阶段搜索没有寻找到目标的情况时，会重新对目标移速进行预估并再次进行第二阶段的搜索，依次类推直到搜索到目标为止。按照本文适应度的计算方法可以求出每一条搜索路径的适应度值。适应度值可以作为衡量搜索路径可靠程度的重要指标。当适应度函数的值等于1的时候，可以认为有100%的概率可以搜索到目标。

6. 总结展望

本文研究了无人机针对移动速度的大小和方向不确定的目标进行搜索的问题，在建立了目标分布概率模型和无人机探测模型的基础上，设计了基于改进遗传算法的无人机搜索路径规划算法。本文的算法和解析方法相比，具有更高的适应性和自动化程度。本文针对移动目标进行的搜索路径规划研究，搜索目标不是单纯的固定目标，是具有一定速度范围的移动目标，并且移动的方向也是不确定的，增强了无人机搜索路径规划的灵活性和实用性。下一步的研究将会着眼于考虑目标变向移动以及环境、天气以及其他特殊原因的影响，考虑无人机飞行高度的不确定性，以此来提高无人机搜索路径规划算法应对各种复杂的搜索环境的适应性。

基金项目

国家自然科学基金(71571190)。