基于最短路径的关键子网选择的加权脑网络分类研究

Research on Classification of Weighted Brain Network Based on Key Subnet Selection of Shortest Path

摘要: 目前，大多数关于轻度认知障碍的分类是以单个脑区在整个脑网络中的局部相关性作为分类特征的，其忽略了多个脑区间相互作用的信息，并且当前绝大部分研究是基于无权脑网络的，丢失了脑区间相互作用的强度。为了更好地捕捉到能区分脑网络的关键拓扑结构信息，本文提出了一种关键子网选择算法，首先计算加权脑网络中的最短路径，并根据正负类样本中最短路径出现的次数差异来选择差异性显著的特征，然后再根据选择出的最短路径上的节点来构建关键子网，最后利用图核对子网数据进行分类。通过将实现了所提出算法的加权脑网络、无权脑网络以及全脑网络进行对比实验，验证了该方法在轻度认知障碍分类上的有效性。

Abstract: At present, most of classifications of mild cognitive impairment are based on the local correlation of a single brain region in the whole brain network, which ignores the information of interaction between multiple brain regions. Moreover, most of the current researches are based on the unweighted brain network, losing the intensity of interaction between brain regions. In order to better capture the key topology information that can distinguish brain networks, this paper proposes a key subnet selection algorithm. Firstly, the shortest path in weighted brain network is calculated, and features with significant difference are selected according to the difference of the number of the shortest path in positive and negative samples. Then, the key subnets are constructed according to the nodes on the selected shortest paths, and finally graph kernel is used to classify subnet datasets. By comparing the weighted brain network, the unweighted brain network that implement the pro-posed algorithm and the whole brain network, the effectiveness of this method in the classification of mild cognitive impairment is verified.

1. 引言

轻度认知障碍(Mild cognitive impairment, MCI)是正常衰老转化为阿尔茨海默病(Alzheimer’s disease, AD)的一个中间过程，每年有高达15%的MCI患者会转化为AD [1] [2] [3]。目前关于脑网络的分类研究主要是以阈值化后的无权脑网络计算的单个脑区的拓扑特征或整个脑网络的效率、紧密程度等作为分类特征，其主要有以下两个方面的缺点：一是无权脑网络通过阈值化的方法，将脑区间相互作用的强度表示为仅由0和1构成的边，因而忽略了两两脑区间关系的强弱，造成了脑网络中部分功能关系信息的丢失；二是单个脑区的特征或全脑网络的效率、紧密度的计算主要是建立在图论的基础之上，并且脑网络本身是一种小世界网络，具有“高聚类、短路径”的特性 [4]，因而可以计算每个脑区节点的聚类系数、特征路径长度等局部连接属性，再经过特征选择，最终用于疾病分类，但此种方法容易导致全脑网络结构信息的丢失。部分研究者利用图核来对MCI患者和正常人的全局脑网络进行相似性分析 [5] [6]，图核可表示疾病引起的脑区间拓扑结构的变化，但全局脑网络包含着许多冗余连接，即使在阈值化处理后，仍不能更准确地刻画脑网络病变部分的关键结构。

为解决上述问题，本文提出了一种基于最短路径的关键子网选择算法。该方法建立在加权脑网络之上，并在阈值化的基础上，保留了脑区节点间的连接强度，进一步利用正负类样本中最短路径出现的次数差异来筛选特征，然后根据选择出的最短路径上的脑区节点构建子网，最终每个脑网络都对应着一个关键子网，该方法既除去了大部分的冗余连接，又保留了脑区间相互作用的信息。关键子网选择方法选择出了疾病引起的脑网络的异常结构，通过利用图核进行相似性判别，可更有效地对疾病进行分类。

2. 相关技术

2.1. 皮尔逊相关系数(Pearson Correlation Coefficient)

皮尔逊相关系数用于反映两个随机变量间的线性相关程度。其计算公式如下：

$r=\frac{{\displaystyle \sum \left(x-\bar{x}\right)\left(y-\bar{y}\right)}}{\sqrt{{\displaystyle \sum {\left(x-\bar{x}\right)}^2{\displaystyle \sum {\left(y-\bar{y}\right)}^2}}}}$ (1)

其中， $\bar{x}$， $\bar{y}$ 分别是向量x，y的均值，r反映的是相关程度，其取值在−1到1之间，r的绝对值越大说明两个随机变量的相关性越强。

2.2. 最短路径

采用典型的基于贪心策略的Dijkstra算法来计算脑网络中的最短路径 [7] [8]。其原理如下：

声明一个数组dis用来保存源点到其他各顶点的最短距离以及一个顶点集合Q用来保存已找到最短路径的顶点。初始时，源点s的路径长度被赋值为0，即dis[s] = 0。对于源点s，若图中存在边(s, v)，则将dis[v]设置为边(s, v)上的权值，并将源点s不能直接到达的其他所有顶点的路径长度设为无穷大。初始时，集合Q中只有源点s。然后，从数组dis中选择最小的值，则该值即为源点s到该值对应顶点的最短路径的长度，并添加该点到集合Q中。接着判断新加入的顶点是否能够到达其他顶点且源点s通过该新加入的顶点到其他点的最短路径是否比从源点直达短。若是，则替换这些顶点在数组dis中的值，再从数组dis中找出路径长度的最小值，重复上述步骤，直至顶点全部遍历完成。

2.3. 图核

图核作为一种反映图数据结构化信息的核函数，既保留了向量核函数的优点，又能够体现出图数据在高维希尔伯特空间中的结构信息 [9]。脑网络作为一种仅由脑区节点和边表示的图数据，可利用图核来对MCI患者和正常人的脑网络结构进行相似性度量，从而进行区分。目前比较常用的图核是Weisfeiler-Lehman子树核，其原理如下：

给定两个图，若图中的顶点未被分配标签，则以每个顶点的度作为该顶点的初始标签，然后在后续的每次迭代过程中，根据前一次迭代后的标签和相邻顶点的标签来更新每个顶点的标签，也即用相邻顶点标签的排序集并行地扩充每个顶点的标签，并将这些扩充后的标签压缩成新的、更短的标签，直到两个图的顶点标签集不同或者迭代次数达到预定义的最大值h，该迭代过程结束。若经过h次迭代后新创建的标签集是相同的，则无法判断两个图是否同构 [10] [11]。

3. 关键子网选择算法的提出

3.1. 关键子网选择算法简介

脑可以被划分为90个大脑区域和26个小脑区域，受疾病的影响，部分脑区发生病变，因而，选择MCI患者和正常人的脑网络中差异性显著的脑区构建关键子网，再利用图核度量关键子网拓扑结构之间的相似度可有效提高MCI疾病诊断的准确率。脑网络中边上的权值反映了脑区之间相互作用的强度，从中计算的最短路径则反映了多个脑区间协同工作的信息。正常人的多个特定脑区协调工作，执行特定的功能任务。MCI患者的部分脑区受病变影响，脑区之间的相互作用关系发生改变，最终导致MCI患者脑网络的拓扑结构不同于正常人的脑网络，因此，MCI患者脑网络中的最短路径会显著地区别于正常人，所以可以利用最短路径的差异来完成对病变脑区的选择，从而构建两类人群的关键子网，并进一步进行判别。

3.2. 关键子网选择算法研究

MCI患者脑网络中最短路径上的节点及条数与正常人相比会有明显差异，因而，存在某一最短路径在所有正类样本中出现的次数多于或者少于在所有负类样本中出现的次数，为此对度量某一最短路径在样本集合中出现的次数做了如式(2)的定义。

$f_q\left(l_s|L\right)=\frac{\left|l_s\right|}{\left|L\right|}$ (2)

其中，L为所有样本构建出的脑网络集合， $l_s$ 为某一样本的脑网络中的某条最短路径， $\left|L\right|$ 为相应的脑网络集合的大小， $\left|l_s\right|$ 为L中包含该条最短路径的样本个数， $f_q\left(l_s|L\right)$ 为该条最短路径在样本集合L中的频度。

由频度的定义可知，若某条最短路径 $l_s$ 在两类样本中的频度差越大，则表明该条最短路径的判别性就越高，利用该判别性高的最短路径上的节点所构建的关键子网的拓扑结构差异就越大，为此利用式(3)来计算脑网络中某一最短路径 $l_s$ 的频度差。

$S\left(l_s\right)=\left|f_q\left(l_s|L_p\right)-f_q\left(l_s|L_n\right)\right|$ (3)

其中， $L_p=\left\{l_{p1},l_{p2},\cdots ,l_{pm}\right\}$ 表示所有正类样本的最短路径集合， $L_n=\left\{l_{n1},l_{n2},\cdots ,l_{nk}\right\}$ 表示所有负类样本的最短路径集合。由上式可知，若 $S\left(l_s\right)=1$，则表示最短路径 $l_s$ 在其中一类样本中存在而在另一类样本中缺失。对 $L_p$ 和 $L_n$ 中的最短路径的判别性得分进行排序后可得：

$S\left(l_p^1\right)\ge S\left(l_p^2\right)\ge \cdots \ge S\left(l_p^m\right)$ (4)

$S\left(l_n^1\right)\ge S\left(l_n^2\right)\ge \cdots \ge S\left(l_n^k\right)$ (5)

为了得到最具判别性的最短路径并利用该条路径上的节点构建关键子网，定义了如式(6)所示的目标函数。

$J\left(R\right)={\displaystyle \underset{\left|\left\{l_p^i|i\le m\right\}\right|\le r_1}{\sum }S\left(l_p^i\right)}+{\displaystyle \underset{\left|\left\{l_n^j|j\le k\right\}\right|\le r_2}{\sum }S\left(l_n^j\right)}$ (6)

其中，R是候选的最短路径集合，并且 $R=R_1\cup R_2$， $R_1\subseteq L_p$， $R_2\subseteq L_n$； $r_1$ 和 $r_2$ 分别表示正、负类样本所选择的特征个数，也即所选择的最短路径的条数。

具体算法流程如下：

①对正类和负类样本组分别计算其脑网络中的所有最短路径，取并集后分别得到候选的最短路径集合 $L_p$ 和 $L_n$；

②对 $L_p$ 和 $L_n$ 中的每一条最短路径，分别利用式(3)计算其判别性得分并按照降序排列，如式(4)和(5)所示；

③根据式(6)选择出式(4)和(5)中判别性得分最高的前 $r_1$ 和 $r_2$ 条最短路径，可得到最优特征子集 $R^{*}=\left\{l_p^i,l_n^j|i\le r_1,j\le r_2\right\}$；

④找出最优特征子集 $R^{*}$ 上的所有节点，取并集并构建所有训练样本的关键子网，得到 $G_{train}=\left\{G_1,G_2,\cdots ,G_N\right\}$。

4. 实验及结果分析

4.1. 数据集

本研究从ADNI数据库获取了114例静息态功能磁共振成像数据来验证方法的有效性，其中包括68例MCI患者和46例正常对照组(Normal Control, NC)。数据采集使用飞利浦医疗系统，参数设置为field strength = 3.0 T；slice thickness = 3.3 mm；echo time (TE) = 30 ms；repetition time (TR) = 3000.0 ms；48 slices。样本信息详情见表1：

Table 1. Sample information details

表1. 样本信息详情

4.2. 脑网络的构建

实验首先利用SPM8 (Statistical Parametric Mapping Software Package 8)对获取到的脑影像进行一系列的预处理操作以方便两组脑影像在同一条件下进行比较 [12] [13]，然后利用IBASPM (Individual Brain Atlases SPM)中的AAL (Anatomical Automatic Labeling)模板来划分脑区 [14] [15]，将大脑划分为116个感兴趣脑区(90个大脑区域，26个小脑区域)，每个脑区代表一个节点，根据脑区中所有体素上的BOLD (The Blood Oxygenation Level Dependent)信号计算平均时间序列，然后计算成对脑区间时间序列之间的Pearson相关系数，Pearson相关系数的大小代表了静息状态下脑区间功能关系的强弱，被定义为脑网络边上的权值。最终，每个样本均被表示成了一个116 × 116大小的加权脑网络。

脑网络在不同的稀疏度下有不同的分类效果，因而，实验设置了一个阈值范围来阈值化得到的原始的加权脑网络，具体包括以下10个阈值：[0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5]。给定一个脑网络矩阵G和阈值T，采用式(7)来阈值化脑网络

$G^{\prime }=\{\begin{array}{l}0,g\left(i,j\right)<T\\ g\left(i,j\right),其他\end{array}$ (7)

对于加权脑网络，若边上的权值小于设定阈值，则删除该边；若权值大于设定阈值，则保留该边且权值不变。加权脑网络再经过关键子网选择算法后得到不同阈值下的加权子网络，重构后的关键子网络的节点和边对应着原脑网络中的节点和边。实验利用Weisfeiler-Lehman子树核作为核主成分分析的核函数来进行降维，然后利用支持向量机进行分类训练和测试。

4.3. 实验结果与分析

4.3.1. 分类效果对比分析

本文通过与以下方法的对比来证明关键子网选择算法的有效性，同时研究权值信息对病变脑区选择的影响。方法一：将未实现关键子网选择算法，直接利用Weisfeiler-Lehman子树核对全脑网络进行相似性判别的方法作为比较方法；方法二：通过阈值化的方法构建不同阈值下的无权脑网络，即若边上的权值小于设定阈值，则删除该边；若权值大于设定阈值，则保留该边并将其阈值化为1，然后利用关键子网选择算法构建不同阈值下的无权子网络，最后进行实验比较。表2列出了上述方法及本文方法在各自最佳阈值下得到的最佳分类效果。

Table 2. Comparison of classification effects of different brain networks

表2. 不同脑网络的分类效果对比

对比分类结果表明，在加权脑网络的基础上，先通过阈值化的方式除去部分冗余连接，然后利用本文方法选择差异性显著的脑区并构建子网络，最后再利用图核进行相似性判别可有效提高轻度认知障碍疾病分类的准确率，表明了提出的基于最短路径的关键子网选择算法的有效性。在无权脑网络上利用关键子网选择算法构建子网与图核直接应用到不同阈值下的全脑网络的方法相比，分类效果有一定的提高，但提高的并不明显。利用本文方法构建的加权子网络与无权子网络的分类效果相比，分类准确率提高了9.8%，表明权值信息对脑网络中最短路径的计算有较大影响，从而影响了病变脑区的选择。图1显示了提出的关键子网选择算法在不同阈值下的加权脑网络和无权脑网络上的分类效果，以及不进行子网选择，直接将图核应用到不同阈值下的全脑网络上的分类效果。图2显示了上述三种类型的脑网络经交叉验证后得到的平均ROC曲线。

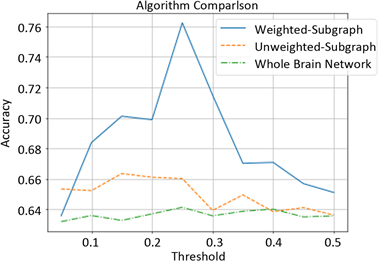
Figure 1. Classification effects of different brain networks under different thresholds

图1. 不同脑网络在不同阈值下的分类效果

Figure 2. Average ROC curve of different brain networks

图2. 不同脑网络的平均ROC曲线

图1表明加权脑网络下的关键子网选择算法对疾病的分类效果明显优于同等实验条件下的无权脑网络以及全脑网络直接应用图核的方法，且在阈值为0.25时的加权脑网络下，实现该算法后的分类效果最好。阈值为0.05时，加权脑网络下的分类效果低于无权脑网络，高于全脑网络下的分类效果，但三者相差的准确率仅在2%的范围内。在阈值小于0.4的范围内，无权脑网络下构建的关键子网的分类效果显著优于全脑网络；在0.4~0.5的阈值范围内，两者的分类准确率相差不大。上述结果表明脑网络中的最短路径反映了部分脑区之间相互作用的关系，受疾病影响，部分脑区的连接关系发生改变致使脑网络的局部拓扑结构出现异常连接，而所提出的基于最短路径的关键子网选择算法能较准确地捕捉到MCI患者和正常人脑网络的结构差异，从而有利于对两组被试者进行区分，证明了该方法的有效性。加权子网络和无权子网络分类效果的对比表明权值信息在较大程度上影响了病变脑区的选择。

4.3.2. Weisfeiler-Lehman子树核迭代次数对比

Weisfeiler-Lehman子树核的迭代次数在一定程度上反映了两组被试者脑网络的拓扑结构是否存在较为明显的差异。若该图核的迭代次数越多，则表明MCI患者和正常人脑网络的结构差异并不明显，需要较多次数的迭代才能将两者区分开；反之，较少的迭代次数表明两组被试者脑网络的结构差异较为明显，仅需要较少的迭代次数便可区分两者。因而，实验记录了不同阈值下的加权子网络、无权子网络及全脑网络达到最高分类准确率时，Weisfeiler-Lehman子树核所需要的迭代次数，具体信息如图3所示。

Figure 3. The number of iterations of different brain networks under different thresholds

图3. 不同脑网络在不同阈值下的迭代次数

本文统计了上述三种类型脑网络的最大、最小以及平均迭代次数，统计结果如表3所示。由表3可知，利用了本文方法得到的加权子网络和无权子网络的最大和平均迭代次数均小于全脑网络相应的迭代次数，且加权子网络和全脑网络的平均迭代次数相差较大，可达4次，由此表明阈值化后的全脑网络仍包含大量冗余信息，而利用关键子网选择算法可以较好地选择出病变脑区，再利用Weisfeiler-Lehman子树核则能够较容易地区分由这些脑区构建的关键子网；加权子网络的平均迭代次数比无权脑网络的平均迭代次数少3次，表明利用加权脑网络中边上的权值信息计算出的最短路径能较为准确地反映脑区之间相互作用的关系，由此构建出的关键子网能较好地反映两组被试者脑网络的拓扑结构差异，从而便于区分两者。虽然三种类型脑网络的最小迭代次数均为1次，但由图3可知，加权子网络、无权子网络和全脑网络的迭代参数为1时出现的次数不同，分别为2次、4次和5次，由此表明了表示脑区之间相互作用强度的权值信息对病变脑区选择的重要性，还表明了所提出的关键子网选择算法能够有效捕捉到MCI患者和正常人脑网络的差异结构，进而利用Weisfeiler-Lehman子树核进行相似性度量并进一步区分。

Table 3. Statistics of iteration times of different brain networks

表3. 不同脑网络的迭代次数统计

5. 结束语

轻度认知障碍疾病影响了患者脑网络的拓扑结构，因而MCI患者脑网络中能反映脑区之间相互作用关系的最短路径会明显区别于正常人，并且由于最短路径的计算会受权值大小的影响，因此提出在能反映脑区之间相互作用强度的加权脑网络中，利用MCI患者和正常人计算的最短路径的差异来选择病变脑区并构建关键子网，最后利用图核进行相似性判别。该方法不仅在一定程度上除去了全脑网络大部分的冗余信息，还弥补了传统无权脑网络的不足。将实现了该算法的加权脑网络与无权脑网络、以及未实现该算法的全脑网络从分类效果和图核迭代次数两个方面进行了对比分析，实验结果证实了所提出的关键子网选择算法能有效捕捉到MCI患者和正常人脑网络的差异结构，从而更好地辅助轻度认知障碍疾病的诊断。