基于亚热带水库生态系统的营养盐–藻类种群生态模型构建及其动力学分析

Establishment and Dynamics Analysis of Nutrient-Algae Ecological Model Based on Subtropical Reservoir Ecosystem

摘要: 基于亚热带水库生态系统中营养盐浓度动态变化特点与藻类种群生长动态特征，为探索营养盐与藻类种群之间的作用机制，构建了一类营养盐–藻类种群生长动态模型，对所建模型进行动态特征分析与数值模拟，研究了模型内平衡点的存在性与稳定性，给出了模型发生Hopf分岔的阈值临界条件，数值模拟出模型所具有的特定动力学行为，验证了理论推导结果的可行性与有效性，揭示了水域生态系统中营养盐动态变化趋势，明确了蓝藻种群与绿藻种群共存生长模型。这些研究工作为进一步研究吴家园水库营养盐动态变化趋势和探索水库优势藻类种群生长动态规律提供一定的理论支撑。

Abstract: In the paper, firstly, on the basic of the dynamic change characteristics of nutrient concentration and algal population growth in subtropical reservoir ecosystem, a nutrient-algae dynamical model was proposed to explore the interaction mechanism between nutrients and algae population. Secondly, the existence and stability of equilibrium points in the model were studied and the threshold critical condition of Hopf bifurcation was given. Thirdly, the specific dynamic behavior of the model was simulated to verify the feasibility and effectiveness of the theoretical results, reveal the dynamic change trend of nutrients in aquatic ecosystem and define the coexistence growth model of cyanobacteria population and green algae population. Finally, these studies can provide theoretical support for further study on the dynamic change trend of nutrients and the growth dynamics of dominant algae population in Wujiayuan reservoir.

1. 引言

从20世纪初，水体富营养化问题就已经引起了生态学家和环境学家的广泛关注，也成为世界至关重要的水环境问题之一，由此而引起的藻类水华问题严重影响当地经济的发展和饮用水安全。如2007年，武汉市蔡甸区发生蓝藻暴发疫情，造成10万公斤鱼类死亡，给当地养殖户造成直接经济损失超过70万元；滇池是昆明饮用水的发源地，1999年滇池暴发水华，湖水变成了“绿色油漆”，该地区的一家水厂因为水华而被迫停产；作为无锡市民饮用水的发源地，2007年太湖暴发蓝藻水华严重影响了无锡人的日常饮用水安全，导致市民家中自来水水质突然发生变化，并伴有难闻的异味，引起市民恐慌，市民纷纷到超市购买纯净水。显而易见，藻类水华的危害与控制问题已成为学术界尤为关注的主要水环境问题之一 [1] [2]。

从20世纪60年代以后，大量研究人员对藻类水华暴发与防控问题做了大量的生态环境研究与种群动力学研究。论文 [3] 指出藻类种群的生长是周期性的，需要经历四个阶段：延迟生长期、指数增长期、稳定生长期和衰退期，并指出盐度、光照、水温和斜坡深度等季节性环境条件对藻类水华暴发具有严重的影响作用。论文 [4] 引入分布时滞来刻画水域生态系统中的时间延迟现象，建立了一类总磷限制下的藻类种群生长动态模型，预测了亚热带吴家园水库营养盐动态演化趋势。论文 [5] 基于反应扩动力系统构建了一类营养盐–浮游植物动态模型，研究了营养盐与浮游植物的时空动力学性态，预测了浮游植物时空动态演化趋势。论文 [6] 引入分布函数来刻画总磷输入季节性变化特征，构建了一类水体富营养化动力系统，预测了亚热带吴家园水库总磷动态演化趋势。论文 [7] 构建了一类具有可变阶分数算子的营养盐–浮游植物动力系统，基于时空扩散动态学形式修正空间动力学效应，研究了毒性对浮游植物空间分布的影响机制。论文 [8] 基于营养盐、浮游植物和浮游动物的相互作用关系，构建了一类营养盐–浮游生物数学模型，揭示产毒浮游植物在水域生态系统中的影响作用。论文 [9] 构建了一类具有延迟和选择性捕获的产毒浮游生物数学模型，探索了此类模型的动力学行为及其种群密度动态演化趋势。论文 [10] 基于生态数据集，构建了一类自下而上的营养盐–浮游植物动力学模型，以帮助了解季节性复发藻类水华的动态趋势，研究结果显示模型具有广泛的动力学行为，从每年触发的简单周期性水华到不规则的混沌水华，即使许多实时时间序列具有这一特征，也极难产生年重复发生且混乱或不规则的藻类水华。

最近几十年来，从种群动力学的角度来探索生态种群相互作用关系获得了前所未有的大发展，最终进入了模型“动力学”的研究时代。论文 [11] 研究了一类具有非单调函数响应的捕食生态时滞系统的一些分岔行为，指出任何时滞值都存在Bogdanov-Takens奇异性。论文 [12] 利用稳定性和Hopf分岔，建立了一类gauss型捕食生态模型，研究了捕食对两类竞争食饵物种的影响作用。论文 [13] 讨论了一类允许食饵避难的捕食生态模型的分岔动力学问题，得到了存在分歧的一些关键条件(Hopf，鞍结，跨临界，Bogdanov-Takens)。论文 [14] 构造了一类分数阶捕食生态系统，研究了系统的稳定性和分岔特性，结果表明适当的食饵捕获量和分数阶导数可以控制混沌动力学并使其趋向稳定。论文 [15] 研究了一类具有非线性收获的捕食生态模型的分岔动力学问题。并对其进行数值仿真，结果表明非线性收获可以使模型的动力学更加复杂，包括双稳态、跨临界分岔和Hopf分岔。此外，大量相关研究者在种群动力学问题和生态数学模型方面也取得了一系列的研究成果，大力促进了本研究方向的快速发展 [16] - [22]。综上所述，生态数学模型和种群动力学模拟取得了前所未有的快速发展，获得了一些有意义和重要的研究成果，但遗憾的是，基于亚热带水库生态系统的水域生态数学模型的发展相对缓慢，尤其是基于种群动力学机制的藻类种群生长动态模型的研究相对较少。

2. 营养盐–藻类动态模型构建

基于亚热带水库野外调查数据与水域生态系统实际运行特征，为建立适应营养盐与藻类种群相互作用机制的数学模型，现在给出一些假设条件。

1) 假设亚热带水库生态系统是一个半封闭的水域生态系统，水库的水体输入与输出都是可以监测的，且输入与输出是可以调控的与大致是一样的，也就是水体体积基本不变，同时营养盐与藻类种群浓度是随着时间的变化而变化，空间分布最终是均匀化的。

2) 营养盐的浓度主要受流入与流出水体中的营养盐含量、底泥释放营养盐的数量和藻类种群对营养盐的吸收等因素所影响，其它影响因素忽略不计。

3) 所关注的藻类种群主要是蓝藻种群和绿藻种群，其它藻类种群的影响忽略不计，且蓝藻种群和绿藻种群存在种群内部竞争关系，不存在种群之间的竞争关系。

4) 参与模型的变量是连续变化的，并且充分光滑。

5) 不考虑其它所有因素对营养盐、蓝藻种群和绿藻种群的影响作用，仅考虑营养盐(氮磷)、蓝藻种群和绿藻种群之间的相互作用关系。

基于上述假设与水域生态系统建模原理，我们将建立一类营养盐–藻类种群生态模型，可以用方程组(1)来表述，

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=I-bx+\frac{x}{1+x}-\frac{a_{1}xy}{b_1+x}-\frac{a_{2}xz}{b_2+x},\\ \frac{\text{d}y}{\text{d}t}=\frac{e_1{a}_{1}xy}{b_1+x}-d_{1}y-c_1{y}^2,\\ \frac{\text{d}z}{\text{d}t}=\frac{e_2{a}_{2}xz}{b_2+x}-d_{2}z-c_2{z}^2\text{.}\end{array}$ (1)

其中x，y和z分别代表水库生态系统中营养盐浓度、蓝藻种群浓度和绿藻种群浓度，b是固定时刻水库

水体输出的流速，I是固定时刻输入水库水体所带营养盐的平均浓度， $\frac{x}{1+x}$ 是水库底淤泥释放营养盐的

函数表达式， $a_1$ 和 $a_2$ 分别是蓝藻种群和绿藻种群对营养盐的吸收率， $c_1$ 和 $c_2$ 分别是蓝藻种群和绿藻种群内部竞争系数， $e_1$ 和 $e_2$ 分别是蓝藻种群和绿藻种群吸收营养盐后转化为自身生长能量的转化率， $d_1$ 和 $d_2$ 分别是蓝藻种群和绿藻种群的自然死亡率， $b_1$ 和 $b_2$ 分别是相应的半饱和系数。同时，为了满足水域生态学意义与实际应用背景，要求模型所有参数取值都大于零，初始值满足 $x\left(0\right)>0,y\left(0\right)>0,z(0)>0$。

3. 理论分析

为了合理地探析营养盐与藻类种群之间的相互作用机制及其相关动力学特性，将对所建生态模型(1)的持久生存性、稳定性和分岔性等动力学行为进行理论分析，推导出模型具有这些特定动力学行为的关键阈值条件，为后续数值模拟工作提供一定的理论基础。

3.1. 种群持久生存性分析

引理1: 若模型(1)的初始值是大于等于零的，则模型(1)的任意解都是大于等于零。

证明：从模型(1)可知，

$\frac{\text{d}x}{\text{d}t}\ge -bx+\frac{x}{1+x}-\frac{a_{1}xy}{b_1+x}-\frac{a_{2}xz}{b_2+x}=x\left(-b+\frac{1}{1+x}-\frac{a_{1}y}{b_1+x}-\frac{a_{2}z}{b_2+x}\right),$

$\Rightarrow x\left(t\right)\ge x\left(0\right){\text{e}}^{{\displaystyle {\int }_0^t-b+\frac{1}{1+x}-\frac{a_{1}y}{b_1+x}-\frac{a_{2}z}{b_2+x}\text{d}t}},$

$y\left(t\right)=y\left(0\right){\text{e}}^{{\displaystyle {\int }_0^t\frac{e_1{a}_{1}x}{b_1+x}-d_1-c_{1}y\text{d}t}},$

$z\left(t\right)=z\left(0\right){\text{e}}^{{\displaystyle {\int }_0^t\frac{e_2{a}_{2}x}{b_2+x}-d_2-c_{2}z\text{d}t}}.$

因此，当 $x\left(0\right)\ge 0,y\left(0\right)\ge 0,z\left(0\right)\ge 0$ 时，对任意 $t\ge 0$，都有 $x\left(t\right)\ge 0,y\left(t\right)\ge 0,z\left(t\right)\ge 0$ 成立。

引理 2. 设 $\Omega =\left\{\left(x,y,z\right):0\le x\le M_1,0\le y\le M_2,0\le z\le M_3\right\}$，则模型(1)的解是有界的。

证明：由模型(1)知， $\frac{\text{d}x}{\text{d}t}\le I-bx+\frac{x}{1+x}\Rightarrow \frac{\text{d}x}{\text{d}t}\le I-bx+1$，根据比较定理可知，

${\lim }_{t\to \infty }\sup x\left(t\right)\le \frac{I+1}{b}=M_1,$

通过以上的分析，以及函数 $f\left(x\right)=\frac{ax}{b+x}$ 的性质可知对于 $\frac{\text{d}y}{\text{d}t}\le \left(\frac{e_1{a}_1{M}_1}{b_1+M_1}-d_1\right)y-c_1{y}^2$ 是成立的，那么

我们就可推得

$\underset{t\to \infty }{\lim }\sup y(t)\le \frac{1}{c_1}\left[\frac{b{e}_1{a}_1\left(I+1\right)}{b{b}_1+I+1}-d_1\right]=M_2.$

同样的有 $\frac{\text{d}z}{\text{d}t}\le \left(\frac{e_2{a}_2{M}_1}{b_2+M_1}-d_2\right)z-c_2{z}^2$，进而得到 ${\lim }_{t\to \infty }\sup z\left(t\right)\le \frac{1}{c_2}\left[\frac{b{e}_2{a}_2\left(I+1\right)}{b{b}_2+I+1}-d_2\right]=M_3$。根据以

上对 $x\left(t\right),y\left(t\right),z\left(t\right)$ 的研究，显然他们都是具有上确界的。我们的定理得到了证明。

定理1. 若条件 $\frac{e_i{a}_i{m}_i}{b_i+m_i}\ge d_i$ 成立，则模型(1)的种群是一致持久生存的

证明：从模型(1)可知，

$\frac{\text{d}x}{\text{d}t}\ge I-bx-\frac{a_{1}xy}{b_1+x}-\frac{a_{2}xz}{b_2+x}\Rightarrow \frac{\text{d}x}{\text{d}t}\ge I-bx-\frac{a_{1}x{M}_2}{b_1+x}-\frac{a_{2}x{M}_3}{b_2+x},$

则

${\lim }_{t\to \infty }\inf x\left(t\right)\ge \frac{I}{b+\frac{a_1{M}_2}{b_1}+\frac{a_2{M}_3}{b_2}}=m_1.$

同样根据函数 $f\left(x\right)=\frac{ax}{b+x}$ 的性质知

$\frac{\text{d}y}{\text{d}t}\ge \left(\frac{e_1{a}_1{m}_1}{b_1+m_1}-d_1-c_{1}y\right)y,$

$\frac{\text{d}z}{\text{d}t}\ge \left(\frac{e_2{a}_2{m}_2}{b_2+m_2}-d_2-c_{2}z\right)z,$

因此

$\underset{t\to \infty }{\lim }\inf y\left(t\right)\ge \frac{1}{c_1}\left(\frac{e_1{a}_1{m}_1}{b_1+m_1}-d_1\right)=m_2,$

${\lim }_{t\to \infty }\inf z\left(t\right)\ge \frac{1}{c_2}\left(\frac{e_2{a}_2{m}_2}{b_2+m_2}-d_2\right)=m_3.$

综上，模型(1)的种群是一致持久生存的。

3.2. 平衡点存在性与稳定性分析

不妨设

$\frac{\text{d}x}{\text{d}t}=I-bx+\frac{x}{1+x}-\frac{a_{1}xy}{b_1+x}-\frac{a_{2}xz}{b_2+x}=P_1\left(x,y,z\right),$

$\frac{\text{d}y}{\text{d}t}=\frac{e_1{a}_{1}xy}{b_1+x}-d_{1}y-c_1{y}^2=P_2\left(x,y,z\right),$

$\frac{\text{d}z}{\text{d}t}=\frac{e_2{a}_{2}xz}{b_2+x}-d_{2}z-c_2{z}^2=P_3\left(x,y,z\right).$

考虑方程 $P_1\left(x,y,z\right)+\frac{1}{e_1}{P}_2\left(x,y,z\right)+\frac{1}{e_2}{P}_3\left(x,y,z\right)=0$ 的解，显然有

$I-bx+\frac{x}{1+x}=\frac{d_1}{e_1}y+\frac{c_1}{e_1}{y}^2+\frac{d_2}{e_2}z+\frac{c_2}{e_2}{z}^2,$

$\Rightarrow \{\begin{array}{l}I-\left(b+1\right)x+\frac{x}{1+x}+M=0,\\ x=\frac{{\left(y+\frac{d_1}{2c_1}\right)}^2}{\frac{e_1}{c_1}}+\frac{{\left(z+\frac{d_2}{2c_2}\right)}^2}{\frac{e_2}{c_2}},\end{array}$

其中 $M=\frac{d_1^2}{4c_1{e}_1}+\frac{d_2^2}{4c_2{e}_2}$。那么我们可以得到

$\{\begin{array}{l}f\left(x\right)=\left(b+1\right)x^2-\left(I+M-b\right)x-\left(I+M\right)=0,\\ 1=\frac{{\left(y+\frac{d_1}{2c_1}\right)}^2}{\frac{e_{1}x}{c_1}}+\frac{{\left(z+\frac{d_2}{2c_2}\right)}^2}{\frac{e_{2}x}{c_2}}.\end{array}$

为了使y和z的相应解都在第一象限内，必须有

$y=-\frac{d_1}{2c_1}+\sqrt{\frac{e_{1}x}{c_1}}>0,$

$z=-\frac{d_2}{2c_2}+\sqrt{\frac{e_{2}x}{c_2}}>0.$

即 $x>\frac{d_1^2}{4c_1{e}_1}$ 且 $x>\frac{d_2^2}{4c_2{e}_2}$ 必须满足。

根据模型(1)可得

$y=\frac{1}{c_1}\left(\frac{e_1{a}_{1}x}{b_1+x}-d_1\right)$ 和 $z=\frac{1}{c_2}\left(\frac{e_2{a}_{2}x}{b_2+x}-d_2\right)$

因此，有

$x>\frac{d_1{b}_1}{e_1{a}_1-d_1}$ 且 $x>\frac{d_2{b}_2}{e_2{a}_2-d_2}\left(e_i{a}_i>d_i,i=1,2\right)$

假定 $H=\max \left\{\frac{d_1^2}{4c_1{e}_1},\frac{d_2^2}{4c_2{e}_2},\frac{d_1{b}_1}{e_1{a}_1-d_1},\frac{d_2{b}_2}{e_2{a}_2-d_2}\right\}$，则当 $x>H$ 时，系统存在第一象限的解，即存在内

平衡点 $E^{*}=\left(x^{*},y^{*},z^{*}\right)$。

定理2. 当内平衡点存在时，若条件(2)~(4)满足，则内平衡点 $E^{*}=\left(x^{*},y^{*},z^{*}\right)$ 是局部渐近稳定的

证明：模型(1)的内平衡点 $E^{*}$ 的雅各比矩阵如下所示：

$J\left(E^{*}\right)=\left[\begin{array}{ccc}A& -E_1& -E_2\\ D_1& -B& 0\\ D_2& 0& -C\end{array}\right],$

其中

$A=\frac{1}{{\left(1+x^{*}\right)}^2}-b-\frac{a_1{b}_1{y}^{*}}{{\left(b_1+x^{*}\right)}^2}-\frac{a_2{b}_2{z}^{*}}{{\left(b_2+x^{*}\right)}^2},B=c_1{y}^{*},C=c_2{z}^{*},$

$E_1=\frac{a_1{x}^{*}}{b_1+x^{*}},E_2=\frac{a_2{x}^{*}}{b_2+x^{*}},D_1=\frac{e_1{a}_1{b}_1{y}^{*}}{{\left(b_1+x^{*}\right)}^2},D_2=\frac{e_2{a}_2{b}_2{z}^{*}}{{\left(b_2+x^{*}\right)}^2},$

可求得其特征方程为

$-{\lambda }^3+\left(A-B-C\right){\lambda }^2+\left(AB+AC-BC-D_1{E}_1-D_2{E}_2\right)\lambda +ABC-D_1{E}_{1}C-D_2{E}_{2}B=0,$

要使该特征方程具有三个负特征根，根据韦达定理知需以下条件成立。

$A-B-C<0,AB+AC-BC-D_1{E}_1-D_2{E}_2<0,$

$ABC-D_1{E}_{1}C-D_2{E}_{2}B<0.$

即

$\frac{1}{{\left(1+x^{*}\right)}^2}-b-\frac{a_1{b}_1{y}^{*}}{{\left(b_1+x^{*}\right)}^2}-\frac{a_2{b}_2{z}^{*}}{{\left(b_2+x^{*}\right)}^2}-c_1{y}^{*}-c_2{z}^{*}<0,$ (2)

$\left[\frac{1}{{\left(1+x^{*}\right)}^2}-b-\frac{a_1{b}_1{y}^{*}}{{\left(b_1+x^{*}\right)}^2}-\frac{a_2{b}_2{z}^{*}}{{\left(b_2+x^{*}\right)}^2}\right]\left(c_1{y}^{*}+c_2{z}^{*}\right)-c_1{c}_2{y}^{*}{z}^{*}-\frac{e_1{a}_1^2{b}_1{x}^{*}{y}^{*}}{{\left(b_1+x^{*}\right)}^3}-\frac{e_2{a}_2^2{b}_2{x}^{*}{z}^{*}}{{\left(b_2+x^{*}\right)}^3}<0,$ (3)

$\left[\frac{1}{{\left(1+x^{*}\right)}^2}-b-\frac{a_1{b}_1{y}^{*}}{{\left(b_1+x^{*}\right)}^2}-\frac{a_2{b}_2{z}^{*}}{{\left(b_2+x^{*}\right)}^2}\right]c_1{c}_2{y}^{*}{z}^{*}-\frac{e_1{a}_1^2{b}_1{x}^{*}{y}^{*}}{{\left(b_1+x^{*}\right)}^3}-\frac{e_2{a}_2^2{b}_2{x}^{*}{z}^{*}}{{\left(b_2+x^{*}\right)}^3}<0.$. (4)

此时，模型(1)具有三个负的特征根，因此内平衡点 $E^{*}=\left(x^{*},y^{*},z^{*}\right)$ 是局部渐近稳定的。

定理3. 若条件(5)~(7)成立，则模型(1)在内平衡点 $E^{*}=\left(x^{*},y^{*},z^{*}\right)$ 处发生Hopf分岔。

证明：根据定理2可知，内平衡点的雅各比矩阵的特征方程为

$-{\lambda }^3+\left(A-B-C\right){\lambda }^2+\left(AB+AC-BC-D_1{E}_1-D_2{E}_2\right)\lambda +ABC-D_1{E}_{1}C-D_2{E}_{2}B=0.$

若该内平衡点处可发生Hopf分叉，则其有一对共轭虚根，设其特征根分别为 ${\lambda }_1,{\lambda }_2,{\lambda }_3$，其中 ${\lambda }_2,{\lambda }_3$ 是一对共轭虚根，令 $g={\lambda }_2{\lambda }_3$ 则该特征方程可写为 $\left(\lambda -{\lambda }_1\right)\left({\lambda }^2+g\right)=0$

经其展开得

$g=-\left(AB+AC-BC-D_1{E}_1-D_2{E}_2\right)>0,$ (5)

${\lambda }_1=A-B-C<0,$ (6)

$g{\lambda }_1=ABC-D_1{E}_{1}C-D_2{E}_{2}B<0.$ (7)

根据公式(7)可解得 $b=b_{*}$。

综上可知，当 $b=b_{*}$ 时，则其特征方程存在一对纯虚根。下面我们证明横结性条件。

设 $\lambda =u+iv$， $H_1=-\left(A-B-C\right)$， $H_2=-\left(AB+AC-BC-D_1{E}_1-D_2{E}_2\right)$， $H_3=-\left(ABC-D_1{E}_{1}C-D_2{E}_{2}B\right)$ 则

${\left(u+iv\right)}^3+H_1{\left(u+iv\right)}^2+H_2\left(u+iv\right)+H_3=0$ (8)

分离方程(7)的实部和虚部并消去v，得

$8u^3+8H_1{u}^2+2\left(H_1^2+H_2\right)u+H_1{H}_2-H_3=0,$ (9)

当 $b=b_{*}$，显然 $u\left(b_{*}\right)=0$ 且 $8u^2+8H_{1}u+2\left(H_1^2+H_2\right)=0$。对公式(9)求关于参数b的导数，则

$\left[24u^2+16H_{1}u+2\left(H_1^2+H_2\right)\right]\frac{\text{d}u}{\text{d}b}+\left(8u^2+4H_{1}u\right)\frac{\text{d}{H}_1}{\text{d}b}+2u\frac{\text{d}{H}_2}{\text{d}b}+\frac{\text{d}}{\text{d}b}\left(H_1{H}_2-H_3\right)=0,$

故，

${\left[\frac{\text{d}u}{\text{d}b}\right]}_{b=b_{\text{*}}}=\frac{-\frac{\text{d}}{\text{d}b}\left(H_1{H}_2-H_3\right)}{2\left(H_1^2+H_2\right)}\ne 0.$

综上，模型(1)在内平衡点 $E^{*}$ 处可发生Hopf分岔。

4. 数值模拟与分析

为了深入探析营养盐与藻类种群之间的相互作用机制，建立比较符合它们动态规律的营养盐-藻类种群生态数学模型，需要对所建模型进行相关动力学模拟试验，验证理论推导结果的可行性，明确所建生态数学模型在研究水域生态环境问题中的适应性与可用性。依据模型建立假设与理论推导结果，以及实验室模拟试验和水库实际操作可行性，我们选择输出流速b作为控制关键参数进行相关动力学模拟试验，其它参数取值为 $I=0.005$， $a_1=0.72$， $a_2=0.65$， $b_1=0.85$， $b_2=0.55$， $e_1=0.53$， $e_2=0.52$， $c_1=0.012$， $c_2=0.01$， $d_1=0.1$， $d_2=0.12$。同时，我们选取初始值为 $x\left(0\right)=0.003$， $y\left(0\right)=0.1$， $z\left(0\right)=0.1$，显然不管是水库或者实验室藻类种群生长动态模拟试验，所建生态数学模型大致描述了每时刻营养盐是以其平均值流入水域生态系统，其浓度是大于所建数学模型的初始浓度，所以属于水域生态系统营养盐逐渐增加的变化状态，也就是说水体富营养化会越来越严重。同时蓝藻种群和绿藻种群都是处于生长的初始阶段，后面是否能够快速繁殖，或者成为藻类水华现象都是未知数。

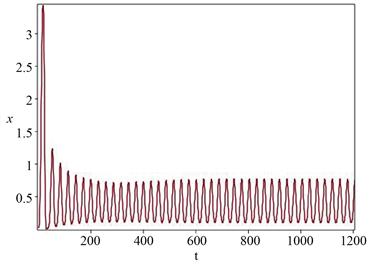
当控制参数b的取值分别为0.1和0.2时，从图1和图2可知，模型(1)分别拥有一个稳定的平衡点和一个稳定的极限环。显然，当控制参数b的取值从0.2减少到0.1时，相位图的定性性质发生了本质的变

(a) (b) (c) (d)

Figure 1. Time series diagram and phase diagram of model state variables (stable limit cycle)

图1. 模型状态变量的时间序列图与相位图(稳定的极限环)

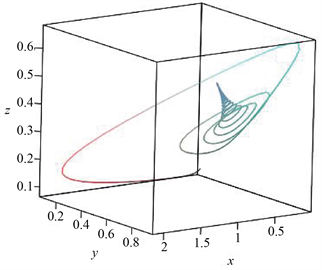(a) (b) (c) (d)

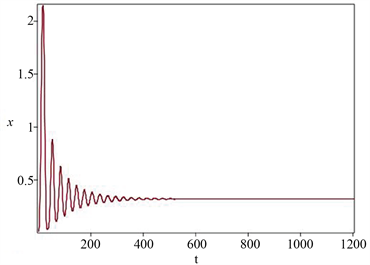
Figure 2. Time series diagram and phase diagram of model state variables (stable equilibrium point)

图2. 模型状态变量的时间序列图与相位图(稳定的平衡点)

化，除了平衡点的稳定性性质发生变化外，还从平衡点分岔出一个极限环，即产生周期振荡，因而模型(1)在内平衡点处发生一个亚临界Hopf分岔动力学行为，这些研究结果验证了定理2和定理3的可行性和有效性。同时，流入水生态系统的水体中营养盐平均浓度高于系统初始浓度，因此，随着时间的增加，水域生态系统的营养盐浓度是逐渐增加的，且最终到达饱和富营养化程度，这个结果可以从图1和图2中看出。此外，当固定时刻流出水质的流速比较低时，蓝藻种群与绿藻种群以周期振荡形式共存，随着流速取值逐渐增加，蓝藻种群与绿藻种群改变为以平衡态形式共存。显然蓝藻种群与绿藻种群的共存模式发生了本质的改变，但其浓度值相对于藻类水华数量级还是较小的，不足以形成藻类水华。总而言之，所建营养盐-藻类种群模型较好地反映出营养盐实际动态变化趋势、蓝藻种群与绿藻种群共存生长模式，比较客观地揭示了在营养盐充足的条件下，蓝藻种群与绿藻种群共存生长模式。

5. 结论

基于亚热带水库野外调查数据与水域生态系统实际运行特征，为探索营养盐与藻类种群之间的作用机制，构建了一类营养盐–藻类种群生态数学模型，对所建生态数学模型进行动态特征分析与数值模拟仿真，研究了模型内平衡点的存在性与稳定性，以及Hopf分岔性，数值模拟出模型所具有的特定动力学性态，验证理论推导结果的可行性与有效性，揭示出水域生态系统中营养盐动态变化趋势，明确蓝藻种群与绿藻种群共存生长模型。这些研究工作为进一步研究吴家园水库营养盐动态变化趋势和探索水库优势藻类种群生长动态规律提供一定的理论支撑。

基金项目

国家自然科学基金(61871293, 31570364, 41876124, 61901303)、国家重点国际合作项目(2018YFE0103700)和苍南县科技计划项目(2018ZG29)、温州市科技重大专项(2018ZG002)。

NOTES

^*通讯作者。