基于GrO^¨bner基方法的乘法器等价性验证

Equivalence Verification of Multipliers Based on GrO^¨bner Basis Method

摘要: 乘法器的等价性验证目前仍是大规模算术集成电路设计领域内的一大难题。本文利用逻辑门与多项式之间的对应关系，构建了乘法器的代数模型，将乘法器等价性验证问题转化成理想成员判定问题，然后再用计算机代数系统中的Gröbner基方法进行求解。提出了一种对乘法器结构进行切片后再采用增量式验证的新方法。在Linux平台上的计算机代数系统Mathematica上所做的实验结果也表明了该方法的有效性。

Abstract: The equivalence verification of multipliers is still a difficult problem in the field of LSI design. In this paper, the algebraic model of multipliers is constructed by using the corresponding relationship between logic gates and polynomials. The problem of equivalence verification of multipliers is transformed into the problem of determining ideal members. Then, the problem is solved by the Gröbner basis method in computer algebra system. This paper presents a new method of incremental verification after slicing the multiplier structure. The experimental results on Mathematica, a computer algebra system on Linux platform, also show the effectiveness of the method.

1. 引言

随着科学技术的发展，集成电路的结构日益复杂，步入SoC时代，在门级抽象层次上已经达到数以百万和千万门系统的设计和验证 [1]。为了保证设计的错误能及时发现，杜绝因重新设计和流片浪费开发成本和设计周期，就需要对电路进行正确性的验证。传统的模拟验证因其不完备性，已经不能适用于现时的较高抽象层次上的集成电路的验证，为了避免“20世纪60年代的软件危机”和“著名的奔腾FDIV错误”此类情况发生，促使人们去研究更完善的验证方法 [2] [3] [4]。

等价性验证是目前在实际的芯片设计中应用最广泛的形式化验证技术，如Synopsys公司的Formality，Mentor Graphics公司的FormalProTM，Cadence公司的Affirma等，并且能处理较大规模的设计 [5]。等价性验证一般采用图表示法和代数表示方法 [6]。图表示法主要使用二叉判定图(BDD)，Brand利用BDD将电路建模为miter，计算所有可达状态这就是典型的基于有限状态机遍历算法 [7]。尽管最近十多年里，由于BDD方法的研究进展使得基于有限状态机遍历算法有了很大进步，但BDD需要大量储存和操作空间的问题仍无法避免，而且用布尔函数表示的状态集会成指数增长，存在状态空间爆炸问题。并且在抽象层较高的等价性验证中，受图形表示能力和图形构造上的制约，BDD无法胜任验证任务。相比而言，基于代数方法的等价性验证则更适合高层次验证。

代数学是数学的一个基本分支，它所处理和研究的数学对象是抽象的代数符号与概念，如整数、有理数、多项式、环、理想等 [8] [9]。其中多项式由于其描述电路时抽象建模能力强，表示具有规范性、无歧义性，使其成为理想的电路建模工具。Buchberger在1915年提出了多项式环上的Gröbner基，因其良序性方面的优势适用于计算机代数领域 [10] [11]。本文运用Gröbner基与乘法器电路结合的思想，在Galois域上采用迭代算法验证整数乘法器电路 [11] [12] [13] [14]。通过实验对比不同方法所需运行时间，易见各方法对乘法器等价性验证的效率影响。

2. Gröbner基理论

对于环R中给定的理想I，其Gröbner基一般并不唯一。这些Gröbner基与项序的选择密切相关，下面给出相关定义 [8] [9] [10]。

定义2.1 设 为任意一个域，变量序列 $x_1,\cdots ,x_n$ 记为X，将含有n个变量的多项式环记为 $k\left[X\right]$ 或 $k\left[x_1,\cdots ,x_n\right]$。

多项式环中最重要的结构为理想，理想为多项式环中的一种子集，其中的元素对加法和乘法封闭。

定义2.2 多项式集合I 是环 $k\left[X\right]$ 的子集，如果满足

(1) $0\in I$，

(2) 如果 $f,g\in I$，则 $f+g\in I$，

(3) 如果 $f\in I,h\in K\left[X\right]$，则 $hf\in I$，

上述条件，则称I为多项式理想。

对于Gröbner基来说，多项式环 $k\left[x_1,\cdots ,x_n\right]$ 中单项式序的概念是一个基本概念，他可以定义出任意多项式的首项，从而保证多项式除法操作下余式唯一。

定义2.3 设 $\alpha =\left({\alpha }_1,\cdots ,{\alpha }_n\right),\beta =\left({\beta }_1,\cdots ,{\beta }_n\right)\in Z_{\ge 0}^n$，集合Τ上的关系 $\prec$ 称为一个单项式序，如果 $\prec$ 满足下面条件：

(1) $\prec$ 为Τ上的一个全序；

(2) $x^{\alpha }\prec x^{\beta },x^{\gamma }\in T$，那么， $x^{\alpha +\gamma }\prec x^{\beta +\gamma }$ ；

(3) $\prec$ 为Τ上的良序，即Τ上每一个非空子集有极小元。

其中 $T=\left\{X^{\alpha }=x_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_n^{{\alpha }_n}|\alpha =\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)\in Z_{\ge 0}^n\right\}$ 是所有单项的集合。

单项式序常见的有三种，字典序，分次字典序，分次逆字典序。

定义2.4 设 $\alpha =\left({\alpha }_1,\cdots ,{\alpha }_n\right),\beta =\left({\beta }_1,\cdots ,{\beta }_n\right)\in Z_{\ge 0}^n$，如果 $\alpha -\beta \in Z^n$ 的最左边非空元素为正数，则称单项式 $x^{\alpha }{\prec }_{lex}{x}^{\beta }$ 为字典序排序。

定义2.5 非零多项式 $f\in k\left[x_1,\cdots ,x_n\right]$ 在给定的单项式序下，可唯一表示为 $f=c_1{x}^{{\alpha }_1}+\cdots +c_n{x}^{{\alpha }_n}$

则称 $LC\left(f\right)=c_1$ 为多项式f的首项系数， $Mulidegree\left(f\right)={\alpha }_1$ 为多项式f的次数， $LM\left(f\right)=x^{{\alpha }_1}$ 为多项式f的首单项式， $Lt\left(f\right)=LC\left(f\right)LM\left(f\right)=c_1{x}^{{\alpha }_1}$ 为多项式f的首项。

定义2.6 在多项式环 $k\left[x_1,\cdots ,x_n\right]$ 上给定一个单项式序，非零理想I的有限子集 $G=\left\{g_1,\cdots ,g_t\right\}$，如果满足

$\langle LT\left(g_1\right),\cdots ,LT\left(g_t\right)\rangle =\langle LT\left(I\right)\rangle$

称G为理想I的Gröbner基。

结合多元多项式除法，Gröbner基理论为理想成员问题提供了一个判定过程：给定一个多项式 $q\in k\left[X\right]$ 和理想 $I=\langle G\rangle =\langle g_0,\cdots ,g_m\rangle \subseteq k\left[X\right]$。通过计算余数是否等于零，则可判定q是否为I中的元素。

3. 代数模型

Buchberger算法利用S-多项式去求多项式的Gröbner基，该算法的时间和空间复杂度是指数级的，在实际应用中是不可行的。因此本文直接将电路建模为Gröbner基多项式。

考虑一个具有l个布尔输入 $a_0,\cdots ,a_{l-1}$ 和m个输出 $s_0,\cdots ,s_{m-1}$ 的电路C。它的每个内部门由一个门变量 $g_0,\cdots ,g_j$ 表示。接下来在相同的布尔输入 $a_0,\cdots ,a_{l-1}$ 下，设电路C'有m个不同的输出 ${s^{\prime }}_0,\cdots ,{s^{\prime }}_{m-1}$。与电路C中每个门(输出)类似，在电路C'中由门变量 ${g^{\prime }}_0,\cdots ,{g^{\prime }}_k$ 表示。

门电路的逻辑门用多项式和信号作为布尔变量建模。其布尔变量之间的多项式关系是

$\begin{array}{l}u=\neg v\iff -u+1-v=0\\ u=v\wedge w\iff -u+vw=0\\ u=v\vee w\iff -u+v+w-vw=0\\ u=v\oplus w\iff -u+v+w-2vw=0\end{array}$ (1)

每个逻辑门都是以门输入变量来描述门输出变量的方式来建模的。

每个多项式的一般形式是：

$p_i=首项\left(x_i\right)+尾部(\; p\; i\; )$

其中首项 $x_i$ 是门的输出变量，尾部 $p_i$ 是由门的输入变量组成的术语。根据这个多项式形式，模型的所有首项都是相对素的。电路是在布尔值范围内操作，因此，对于变量u，可得到关系式 $u\left(u-1\right)=0$。满足等式左侧的多项式编码形式称为域多项式F。

定义3.1 设 $G\in k\left[X\right]$ 是满足(1)的对应多项式的电路C每个门的集合，并且多项式 $a_i\left(a_i-1\right)$ 和 $b_i\left(b_i-1\right)$ 称为输入域多项式， $0\le i<n$。则 $G\in k\left[X\right]$ 中生成的理想用 $J\left(C\right)$ 表示。

定义3.2设C是一个电路。一个多项式 $p\in k\left[X\right]$ 被称为电路C的多项式电路约束(PCC)，如果把 $\left(a_0,\cdots ,a_{n-1},b_0,\cdots ,b_{n-1}\right)\in {\left\{0,1\right\}}^{2n}$ 和结果值 $g_0,\cdots ,g_k,s_0,\cdots ,s_{2n-1}$ 带入多形式p得0。

定义3.3 电路C被称为乘法器，如果满足 ${\displaystyle {\sum }_{i=0}^{2n-1}{2}^i{s}_i}-\left({\displaystyle {\sum }_{i=0}^{n-1}{2}^i{a}_i}\right)\left({\displaystyle {\sum }_{i=0}^{n-1}{2}^i{b}_i}\right)$ 是PCC。

本文针对于简单部分积生成的乘法器，其中部分积是指由两个电路输入通过与门产生的输出。为了从Gröbner基中消除带有部分积的这些多项式，把定义3.3中乘法器的规范改为推论3.1中规定的规范。

推论3.1 电路C是乘法器，如果满足 ${\displaystyle {\sum }_{i=0}^{2n-1}{2}^i{s}_i}-{\displaystyle {\sum }_{i,j=0}^{n-1}{p}_{i,j}}\in J\left(C\right)$，其中 $p_{i,j}=a_i{b}_i$。

通过展开定义3.3中的和式，并在推论3.1中用 $a_i{b}_i$ 替代 $p_{i,j}$，很容易地验证推论3.1的正确性。

乘法器的结构包括多个全加器及半加器，下面就以简单的全加器为例，给出理想成员问题判定过程：

例1：实现图1所示功能 $s_i+2c_i=a_i+b_i+c_{i-1}$ 的全加器电路。

Figure 1. Full-add circuit

图1. 全加器电路

根据(1)，得图1的代数模型是

$g_1:=-c_i-x_4{x}_3+x_4{x}_3,g_2:=-s_i-2x_1{c}_{i-1}+x_1+c_{i-1}$

$g_3:=-x_4+x_2{c}_{i-1},g_4:=-x_3+a_i{b}_i,$

$g_5:=-x_2-a_i{b}_i+a_i+b_i,g_6:=-x_1-2a_i{b}_i+a_i+b_i$

其中规范多项式为 $p_{spec}=-2c_i-s_i+c_{i-1}+b_i+a_i$，将多项式变量按电路的逆拓扑顺序 $a_i\prec b_i\prec c_{i-1}\prec x_1\prec x_2\prec x_3\prec x_4\prec s_i\prec c_i$ 排序，在此序下，用规范多项式 $p_{spec}$ 归约代数模型 $g_i$ ：

$p_{spec}\stackrel{g_1}{\to }-s_i+2x_4{x}_3-2x_4-2x_3+c_{i-1}+b_i+a_i$

$\stackrel{g_2}{\to }2x_4{x}_3-2x_4-2x_3+2x_1{c}_{i-1}-x_1+b_i+a_i$

$\stackrel{g_3}{\to }2x_3{x}_2{c}_{i-1}-2x_3-2x_2{c}_{i-1}+2x_1{c}_{i-1}-x_1+b_i+a_i$

$\stackrel{g_4}{\to }2x_2{c}_{i-1}{b}_i{a}_i-2x_2{c}_{i-1}+2x_1{c}_{i-1}-x_1-2b_i{a}_i+b_i+a_i$

$\stackrel{g_5}{\to }2x_1{c}_{i-1}-x_1+4c_{i-1}{b}_i{a}_i-2c_{i-1}{a}_i-2c_{i-1}{b}_i-2b_i{a}_i+b_i+a_i$

$\stackrel{g_6}{\to }0$

通过计算得余数为0，因此提取的代数模型为Gröbner基。为了更好的加快验证效率，下节将介绍Gröbner基的约化。

4. 加法器重写

通常情况，关于生成的Gröbner基归约规范，会导致中间约化结果中单项式的数量急剧增加，而影响验证效率 [9] [15]。因此我们利用加法器重写，以便更有效约化Gröbner基 [12]。

首先在乘法器的门级表示中识别全加器和半加法器，并将它们视为独立电路。然后应用变量消去，即用相应的加法器规范来代替全加器和半加法器内部门的所有多项式。这会使表示整个乘法器的Gröbner基更小、更紧凑，从而加快了归约过程。

定义4.1 一个电路C被称为全加器，如果满足 $-2c-s+a+b+i$ 是PCC；相应地，一个电路 被称为半加器，如果满足 $-2c-s+a+b$ 是PCC。其中 $c,s$ 表示输出， $a,b,i$ 表示输入。

例2 给出简单全加器电路 相应的规范多项式：

$H=\left\{-c+g_1+g_2-g_1{g}_2,-s+g_0+i-2g_{0}i,-g_2+ab,-g_1+g_{0}i,-g_0+a+b-2ab\right\}$

那么H是 $J\left(A\right)=\langle H\rangle$ 关于序 $a<b<i<g_0<g_1<g_2<s<c$ 的Gröbner基。

为了消除内部变量 $g_0,g_1,g_2$，直接将输出 $s,c$ 表示为加法器输入 $a,b,i$ 的多项式。下面就给出相关定义和定理，其中R表示环 $k\left[a,b,i,s,c,g_0,g_1,g_2\right]$ 和 $R_{elim}$ 表示环 $k\left[a,b,i,s,c\right]$ [9]。

定义4.2 给定 $J\subset R$，消去理想 $J_{elim}$ 是 $R_{elim}$ 的理想，定义 $J_{elim}=J\cap R_{elim}$ [9]。

定理4.1 设 $J\subset R$ 为理想， $H^{\prime }$ 是J关于序 $a<b<i<s<c<g_0<g_1<g_2$ 的Gröbner基。那么集合 $H_{elim}=H^{\prime }\cap R_{elim}$ 是消去理想 $J_{elim}$ 的Gröbner基 [9]。

例1 (续) 为了消除变量 $g_0,g_1,g_2$，从H中删除涉及这些变量的多项式是不可行的。因此我们根据定理4.1中给定的序，去计算第二个Gröbner基 $H^{\prime }$。再从 $H^{\prime }$ 中删除涉及 $g_0,g_1,g_2$ 的多项式，得

$H_{elim}=\left\{-2c-s+a+b+i,-s+a+b+i-2ab-2ai-2bi+4abi\right\}$.

由定理4.1， $H_{elim}$ 是 $J_{elim}\left(A\right)$ 的Gröbner基，则Gröbner 基就通过加法器重写得以化简。值得一提的是，对于本文研究的能完全分为全加器和半加法器的乘法器，可以约化首项是全加器或半加法器的和输出多项式，如 $H_{elim}$ 中多项式 $-2c-s+a+b+i$ 就可以被首项是 $-s$ 的多项式约化。将其从Gröbner基中消除会带来进一步的改进，但Gröbner基消除该方法有失完备性。

5. 增量式等价性验证

本节引入了一种基于电路列式切片的增量验证将乘法器电路的整体Gröbner基划分为2n个更小的切片Gröbner基。将问题分解为更小的2n个子问题，逐个解决 [15] [16]。

定义5.1 设C和C'是两个电路，如果 $s_i-{s^{\prime }}_i$ 是一个PCC ( $i=0,1,\cdots ,m-1$ )，那么电路C和C'是等价的，记为 $C\equiv C^{\prime }$。

引理5.1 $C\equiv C^{\prime }$ 当且仅当 ${\displaystyle {\sum }_{i=0}^{m-1}{2}^i\left(s_i-{s^{\prime }}_i\right)}\in J\left(C\cup C^{\prime }\right)$。

引理5.2 设C和C'是 两个电路，G和 $G^{\prime }$ 是理想 $J\left(C\right)$ 和 $J\left(C^{\prime }\right)$ 关于序 $\prec ,{\prec }^{\prime }$ 的Gröbner基。设 ${\prec }_{{{\displaystyle \cup }}^{\text{}}}$ 是一个反向拓扑序，使得 $\prec ,{\prec }^{\prime }$ 属于 ${\prec }_{{{\displaystyle \cup }}^{\text{}}}$ 中。那么 $G\cup G^{\prime }$ 是理想 $J\left(C\cup C^{\prime }\right)$ 关于 ${\prec }_{{{\displaystyle \cup }}^{\text{}}}$ 的Gröbner基。

本文中的增量式等价性验证技术，使用切片和切片Gröbner基的定义 [15]。对电路进行切片，进而进行增量式的等价性验证，由于电路 $C\cup C^{\prime }$ 的和的规范可能是未知的，或者无法在Z上以规范和抽象形式表示，不能使用对给定规范执行理想成员的资格测试。因此将 $C\cup C^{\prime }$ 和表示为多项式集，并将它们的Gröbner基组合成一个模型 $G_{{{\displaystyle \cup }}^{\text{}}}=G\cup G^{\prime }$。然后将问题转化为测试 $G_1$ 和 $G_2$ 关于 $G_{{{\displaystyle \cup }}^{\text{}}}$ 中变量之间的成员关系。

定义5.2 设是C和C'上述的两个电路

1) 对于每对输出位s和s'，我们确定其输入锥，即与门，其依赖于：

$I_i=\left\{门g|g在输出s或s^{\prime }的输入锥\right\}$

2) 切片 $S_i$ 定义为连续锥 $I_i$ 的差：

$S_0:=I_0$

$S_{i+1}:=I_{i+1}\setminus {\displaystyle \underset{j=0}{\overset{i}{\cup }}{S}_j}$

若 $G_i$ 是切片 $S_i$ 中电路C和C'的门 的多项式集，则易证 $G_i$ 是切片 $S_i$ 的Gröbner基。

定义5.3 设C和C'是上述两个电路，在其变量上m个 ${\Delta }_0,\cdots ,{\Delta }_m$ 的多项式序列称为切片多项式序列，如果

$-{\Delta }_i+2{\Delta }_{i+1}+\left(s_i-{s^{\prime }}_i\right)\in J\left(C\cup C^{\prime }\right)$， $\left(0\le i\le m\right)$

那么多项式 $E_i=-{\Delta }_i+2{\Delta }_{i+1}+\left(s_i-{s^{\prime }}_i\right)$ 就称为 ${\Delta }_0,\cdots ,{\Delta }_m$ 序列的切片关系。

定理5.4 设C和C'是上述两个电路， ${\Delta }_0,\cdots ,{\Delta }_m$ 是定义4.3中定义的切片多项式序列。那么根据引理5.1，C和C'是等价的( $C\equiv C^{\prime }$ )当且仅当 $2^m{\Delta }_m-{\Delta }_0\in J\left(C\cup C^{\prime }\right)$。

证明：

根据定义5.3，得 $J\left(C\cup C^{\prime }\right)$

${\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{2}^i\left(s_i-{s^{\prime }}_i\right)}={\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{2}^i\left(2{\Delta }_{i+1}-{\Delta }_i\right)}=2^m{\Delta }_m-{\Delta }_0$

设边界 $2^m{\Delta }_m=0$

${\Delta }_{m-1}=\left[2{\Delta }_m+\left(s_m-{s^{\prime }}_m\right)\right]\%G_{m-1}$

${\Delta }_{m-2}=\left[2{\Delta }_{m-1}+\left(s_{m-1}-{s^{\prime }}_{m-1}\right)\right]\%G_{m-2}$

$⋮$

${\Delta }_0=0$

这确保了所有的 $E_i$ 都在 $J\left(C\cup C^{\prime }\right)$ 中。 $J\left(C\cup C^{\prime }\right)$ 包含所有的域多项式F，因此将它们添加到 $G\cup G^{\prime }$ 中。最后，计算是否 ${\Delta }_0=0$。下面给出算法：

根据定理5.4，我们能推导出增量等价性验证算法。先固定边界 $2^m{\Delta }_m=0$，并通过计算切片Gröbner基的 $2{\Delta }_{i+1}+s_i-{s^{\prime }}_i$ 模的余数递归地导出 ${\Delta }_i$， $E_i\in J\left(C\cup C^{\prime }\right)$。通过计算最后 ${\Delta }_0$ 的结果。如果 ${\Delta }_0=0$，则乘法器电路C和C'是等价的。

6. 实验

本文对两类整数乘法器进行等价性验证，分别是btor乘法器和sp-ar-rc乘法器。这两个乘法器都是根据推论3.2中的部分积作为两个输入位，然后由全加器和半加法器进行累加，如图2所示。

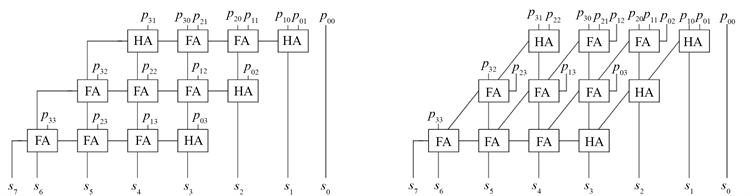
Figure 2. Structure of btor (left) and sp-ar-rc multipliers for $n=4$ with $p_{ij}=a_i{b}_j$

图2. 具有 $p_{ij}=a_i{b}_j$ 的 $n=4$ 的btor乘法器(左)和sp-ar-rc (右)乘法器的结构

图2是 $n=4$ 的4位两输入的实验验证的两类乘法器的结构。在btor乘法器中，全加法器和半加法器以网格状结构累积(图2左侧)；而在sp-ar-rc乘法器中，全加法器和半加法器是对角累积的(图2右侧)。我们使用工具aigmultopoloy [15]，该工具以电路的AIG表示作为输入，并返回一个包含计算指令的文件。由于Mathematica输入语言更灵活，支持更多变量，被用作计算机代数系统，因而本文将这些指令传递给Mathematica。

实验使用了一台带有Ubuntu18.04虚拟机的笔记本电脑，配备Intel i5-8250 1.60 GHz CPU和4 GB主内存。运行时间限制设置为1200秒，主内存使用限制为4 GB。实验中的时间均以秒为单位列出。我们测量从aigmultopoloy开始到Mathematica 完成的时间，包括该aigmultopoloy工具生成Mathematica文件所需的时间和计算机代数系统的启动时间。在实验数据中用TO表示达到时间限制、MO表示达到内存限制、EE表示状态错误。

如表1所示，无论是Lingeling还是ABC在n大于8位时，都超出实验设定的运行时间，而增量方法能验证达32位的这两类乘法器的等价性 [16]。在此基础上添加加法器重写(第六列)，不仅能计算高达128位的等价性，同时8~32位乘法器的等价性验证也有着明显的加快。表中最后一列，不仅采用增量验证方法，还利用第四节中提到的Gröbner基消去，实验数据显示，与第六列相比对各位数乘法器的验证时间均略具优势。

Table 1. Equivalence checking

表1. 等价性验证

7. 结论

本文基于Gröbner基着眼于结构相似的乘法器，采用了增量式的等价性验证算法。在这个基础上，添加加法器重写和Gröbner基消去的算法相关实现，并已于Linux系统中成功编译。实验对比不同方法进行等价性验证的运行时间，由实验数据易见，增量等价性验证能提高验证效率，并在此基础上进一步进行优化，其验证时间略具优势。未来如何将这些技术扩展到浮点运算，甚至更具挑战性的乘法器结构和其他算术电路还有待进一步研究。

NOTES

^*通讯作者。