1. 引言
白内障是当今世界常见的致盲眼病之一,临床上针对白内障有多种治疗方法,但术后眼部结构不稳定,并发症较多,视力质量降低,眼球作为一种十分精密的器官,包含多种组织结构,不同患者眼球结构特征参数(半径、厚度)存在一定差异,全面地了解眼球结构以及形态变得至关重要 [1]。目前国外已经建立了多种眼模型,但大部分都以眼球的光学结构为基础 [2],各模型几何形状也有轻微变化,Charles和Brown建立的眼模型没有考虑到虹膜和巩膜结构;Worgul眼模型仅仅只提供了虹膜的几何形状 [3],这些模型并不能很好地反映真实状态下正常人眼的活动状态,结果存在一定误差,同时也缺乏符合我国人眼特征的个性化眼模型 [4]。随着手术技术和眼科临床水平的不断提高,白内障患者对术后人眼的屈光能力的要求也进一步提高,急需建立可以适用于术前准确、可靠的个性化眼模型 [5]。
眼球的机械性能以及各结构之间的相互交错所带来的力学反应,如角膜的非线性以及粘滞性 [6],晶状体囊膜的粘弹性、应力应变的双线性 [7] 等生物力学特征对白内障手术的开展有着重要作用。眼球从外到内可以分为眼球壁,眼内腔和眼中内容物三部分;眼球最外层的为角膜和巩膜,内部由虹膜、睫状体、脉络膜依次衔接,角膜具有复杂的几何结构,厚度并不均匀,顶点中心处是最薄的,随着靠近角膜缘厚度具有增加的趋势 [8],作为光学系统的一部分,对光线具有一定的屈光功能;晶状体为一个类似于凸透镜的弹性体,作为白内障发生病变最主要的部位,使得患者眼球的各结构介质发生改变 [9]。图1为眼球的解剖图。
Gullstrand I号模型眼 [10] 作为视觉领域最早出现、应用最多的一种模型眼,展现了角膜、晶状体皮质、晶状体核的前、后共6个折射面,很大程度上接近于真实人眼的状态,表1给出了模型眼的结构参数。

Table 1. Gullstrand I eye model structure parameters
表1. Gullstrand I号模型眼结构参数
本文针对白内障超声乳化术后产生的晶状体囊膜皱缩并发症,基于早期的Gullstrand I号模型眼,提出一个基于二次曲面方程的数学描述的方法,考虑到眼球的结构并减少角膜的球差对屈光能力的影响,并对构建的人眼几何模型划分网格,进行相关的有限元分析,有助于帮助临床上白内障相关手术的训练,提高解决此问题的有效性和可行性,更适合白内障手术的临床应用。
2. 基于眼球结构数学特征的模型建立
本文根据不同文章中给出的眼球特征参数建立个性化眼模型,能表现人眼的屈光能力相较于各结构参数数据精确性显得更为重要,因此选取眼球各结构相对曲率半径、厚度等作为基本特征,具体相关参数如表2。


Table 2. Reference value of eyeball characteristic parameters
表2. 眼球特征参数参考值
Duke-Elder认为巩膜整个曲面的曲率半径大小相等,而角膜曲率半径相较于巩膜偏小,角膜基于前巩膜孔的两点向前突出,略大于巩膜曲率半径所成的圆 [16]。眼球的每个曲面根据各结构的特征参数,都有一个自身的数学表达式。二次曲面模型的公式 [17] 均可表示为:
式中,R代表曲面的曲率半径,Q为非球面的参数;x,y,z分别为空间中点的坐标,z轴默认为光学轴。
由于各结构有着不同的本质特性,曲率半径、厚度以及表面规则这三种基本成分直接影响了其数学表达式的结果,依次分析各结构的形态特征,建立可描述各结构形态特点的数学模型。角膜从中心顶点到靠近角膜缘处呈现厚度不均的变化,James重建角膜轮廓的实验确定角膜表现为椭圆形 [18],这些差异决定了其非球面的特性。视网膜、脉络膜、巩膜为整个眼球的轮廓,大致呈球形,且赤道前后巩膜、脉络膜、视网膜的曲率一致,确定其为球面的特性。晶状体真实形状结构复杂,弹性变化浮动较大,测量数据采用解剖人眼以及现有存在的晶状体参数,假设晶状体为旋转的一个系统。以眼球的轴长作为基本变量,利用轴长与其他各结构的线性关系 [16],建立基于二次曲面的人眼数学模型,设眼球的对称中心作为原点,以眼球水平方向为x轴,眼球垂直方向为y轴,人眼的光轴为z轴,建立眼球的笛卡尔空间坐标系。将巩膜的内外曲率半径作为眼球整体形态的半径,确定眼球的基本轮廓。计算眼房与晶状体之间的相对距离确定晶状体的具体位置坐标,得到晶状体核以及晶状体囊膜的轮廓曲线。基于巩膜、脉络膜、视网膜、虹膜的相对位置,由各部分的曲率半径确定相对应的轮廓半径,最终获得整个眼球各结构的轮廓曲线方程,以方程式的形式描述人眼各种结构的几何形状,并进一步扩展为三维实体眼模型,实现参数化眼模型的建模。
3. 基于二次曲面方程的个性化眼球有限元模型
3.1. 眼球结构的几何模型
在临床应用方面,白内障手术中晶状体的更换以及囊膜的修复等手术,均是术前建立眼模型,从眼模型上进行模拟,因此研究白内障病人眼球的几何结构显得尤为重要。几何模型是眼球进行手术虚拟仿真的基础,它包括眼球的形态、粗糙度等要素,通常来源于临床的各种实验直接测量得到眼球的特征数据 [19],提取出眼球结构的主要形态参数,通过变换以及运算生成人眼的规则模型。由于眼球器官的特殊性,考虑将眼球作为具有旋转对称性的二次曲面,每一个曲面由曲率半径及面形来定义,基于数学方程表达式来描述人眼轮廓结构,进行表面轮廓的绘制。具体实施方案如下:
1) 以巩膜的中心为圆心1,R1 = 11.74 mm和R2 = 10.74 mm为半径画弧,确定巩膜的内、外轮廓以及脉络膜的外轮廓曲线方程。
2) 以圆心1继续为对称圆心,R3 = 10.3304 mm为半径画弧,确定脉络膜的内轮廓及视网膜的外轮廓曲线方程。以R3 = 10.2673 mm为半径画弧,确定视网膜的内轮廓曲线方程。
3) 圆心1沿光轴正向移动4.575 mm得到圆心2,并以长轴a = 8.7335 mm,短轴b = 8.6278 mm,焦距c = 9.6835 mm绘制角膜前表面;以长轴a = 8.4693 mm,短轴b = 8.2563 mm,焦距c = 11.58481 mm绘制角膜后表面,确定角膜的外轮廓及内轮廓曲线方程。
4) 圆心1沿光轴反向移动12.1033 mm得到圆心3,并以R6 = 21.0039 mm,R7 = 20.7093 mm为半径画弧,确定虹膜的外轮廓及内轮廓曲线方程。
5) 圆心1沿视觉光轴反向移动1.494 mm得到圆心4,并以R8 = 10 mm,沿视觉光轴正向移动10.506 mm得到圆心5,R9 = 6 mm为半径画弧,确定晶状体前囊膜、后囊膜轮廓曲线方程。
6) 圆心1沿视觉光轴正向移动6.5 mm得到圆心6,并以长轴a为2.55 mm,短轴b为1.25 mm,确定晶状体内核的轮廓曲线方程。
个性化人眼的几何模型如图2所示。
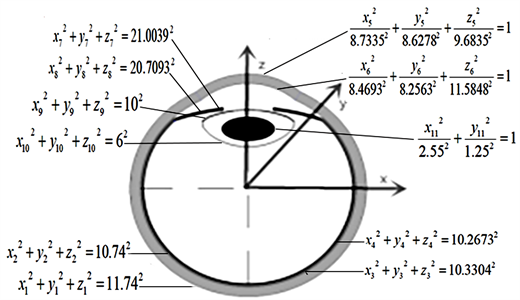
Figure 2. Geometric model of the human eye
图2. 人眼几何模型
3.2. 个性化眼球的有限元模型
为了实现眼球结构的动态性,增大眼模型的精确性,在眼球几何模型的基础上增加眼球内部各结构的物理属性,这对眼球有限元模型的建立至关重要。基于人眼的二维模型,以视觉光轴为旋转轴,利用SOLIDWORKS对人眼的几何模型截面轮廓的参数数据进行旋转,得到人眼的三维立体模型,增大了人眼模型的真实感,很大程度上实现了人眼内外结构的观测,如图3所示。
通过对所建立的眼球结构有限元模型,结合WORKBENCH软件,添加眼球结构相应的密度、弹性模量、泊松比等材料属性并进行网格的划分,得到个性化眼球的有限元模型,进行白内障手术变化过程的研究,为个性化眼模型的应用提供一定的参考价值。为了确保眼模型仿真过程的精确度,同时生动形象地表现手术中角膜变形过程的实时性,对人眼模型的材料属性及网格划分的方式进行了选择,本文选取材料的弹性模量为1.45 Mpa,泊松比为0.47,密度为1.07 kg/m3。由于角膜厚度不均,当选取划分的网格尺寸超过0.20 mm时,网格会产生一定的畸变,质量较差,影响后续仿真的精确性,本文选取以六面体为主导的网格划分方式,并对角膜以及周缘进行加密,网格尺寸确定为0.16 mm,其他结构网格尺寸确定为0.20 mm,最终得到的眼模型共包含1,269,756个节点和384,270个单元,网格划分图如图4所示。

Figure 3. A three-dimensional model of the human eye
图3. 人眼的三维立体模型
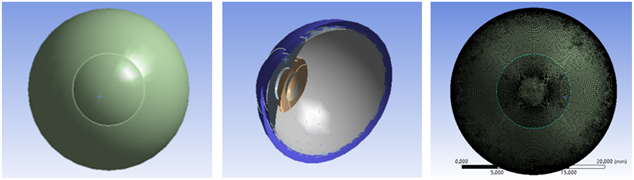
Figure 4. Diagram of meshing of eye model
图4. 眼模型网格划分示意图
白内障手术时角膜受到外部撕囊镊的挤压,因此在模型外部施加载荷模拟手术初始过程,眼模型受到载荷的作用经历压平、凹陷、回到初始状态的过程,变化如图5所示。

Figure 5. Corneal vertex deformation in eye model
图5. 眼模型中角膜顶点受力变形
对角膜顶点受力变形位移的变化情况汇总,得到表3如下。本文以有限元仿真结果作为验证标准,通过比较角膜顶点以及角膜表面节点27的受力变形效果以及位移情况,发现受力大小与位移呈线性变化,与真实状态下角膜受力变化相似,大致符合角膜的生物力学特征变化,表明了眼模型的有效性,可为白内障手术训练的开展提供技术支撑。

Table 3. Corneal apex force displacement
表3. 角膜顶点受力位移变化表
4. 结果分析与讨论
现阶段存在的眼模型大都是轴对称的系统,很难展现非对称因素对手术过程的影响,基于我国的人眼特点,认识到角膜所呈现的是一个椭球面系统,将角膜与人眼其他结构分开设计,角膜以椭球面的形态结构建立数学方程进行描述,减少球面系统所带来的球差影响,并根据人眼各结构拥有的曲面轮廓,研究中为了简化过程,除角膜及晶状体结构外,其他均使用了球形的二次曲面方程对眼模型做了假设,来反映人眼的空间形态,在赋予各结构特征参数时,设置为固定值,但实际人眼的数据并不完全一致,会受到人眼的不同结构特性的影响,在接下来的研究中,将对参数做进一步优化,为人眼模型的研究打下基础。
本文模拟手术过程中手术仪器对人眼施加向内力的过程,首先使角膜向内产生凹陷的变形,并展示了人眼模型中的节点位移变化以及结构形变,通过有限元实验对人眼模型进行仿真验证,施加的载荷大小会影响到人眼模型内部其他结构的位移,同时影响到外部表面的位移方向,因此,人眼模型可为医生进行手术开展提供更好的训练以及手术方案的确定,满足手术的仿真需求。与目前临床上所应用的眼模型进行对比,个性化眼模型以眼球部分结构的相关特征参数为基础,引入了眼球的几何建模,实现了个性化人眼的有限元仿真模型的建立,基于Gullstrand I号模型眼的光学参量,较好地表现了眼球的空间形态特征,为虚眼模型的发展提供了基础,对眼科手术的发展具有重要意义,后期随着数据类型的增加,形态结构也更加符合真实人眼。