温度依赖功能梯度Timoshenko梁的弹塑性屈曲

Elastoplastic Buckling of Temperature Dependence Functionally Graded Timoshenko Beam

摘要: 考虑功能梯度材料物性参数的温度依赖性研究变化的温度场中陶瓷-金属功能梯度Timoshenko梁的弹塑性屈曲特性，其中功能梯度材料的弹塑性材料参数由TTO模型模拟、弹塑性本构方程应用线性强化模型建立。研究中利用Hamilton系统中的辛方法将问题转换为求解正则方程，临界载荷和屈曲模态对应于正则方程的辛本征值和辛本征解。精确解析求解正则方程得到梁的临界载荷和屈曲模态，并结合屈服条件获得弹塑性分界面。最后进行参数研究分析了梯度参数、几何参数和边界条件对该复合材料梁的屈曲载荷和屈曲时弹塑性变形分界面的影响。

Abstract: The elastoplastic buckling characteristics of functionally graded Timoshenko beams in varying temperature field are studied by considering the temperature dependence of material parameters. The elastoplastic material parameters of functionally graded materials are simulated by TTO model and the elastoplastic constitutive equation is established by linear strengthening model. By using the symplectic method in Hamilton system, the problem is transformed into solving canonical equations. The critical load and buckling mode correspond to the symplectic eigenvalue and eigen solution of the canonical equations, and are obtained by accurate analytical solution. At the same time, the elastoplastic interface is obtained by combining the yield condition. Finally, the influence of gradient parameters, geometric parameters and boundary conditions on the buckling load and elastoplastic deformation interface of the beam is analyzed.

1. 引言

功能梯度材料(FGM)是一种可设计的新型复合材料，其材料特性在特定方向上平滑连续变化。FGM在热环境中工作时，可以避免因温度的变化导致应力集中甚至结构失稳的发生。目前为止，已有大量关于FGM结构稳定性的研究论文发表，但大多仅限于弹性稳定性方面。例如，文献 [1] 和文献 [2] 采用有限元法分别研究了FGM板和FGM圆柱壳的弹性屈曲。文献 [3] [4] [5] 采用打靶法等分别研究了FGM圆板、环板和梁的弹性热屈曲、动态屈曲及后屈曲。文献 [6] [7] 运用了摄动法研究了弹性FGM圆柱壳的热后屈曲和FGM板的后屈曲。文献 [8] 研究了FGM梁的热屈曲问题，求得临界屈曲温度。

以上关于FGM结构屈曲的研究尚局限于弹性范围内。若结构厚度尺寸较大，内部应力也较大，同时由于作为FGM重要组分的金属是塑性材料，它的存在极易使结构在应力较大的区域产生塑性变形，发生弹塑性屈曲。目前有少量关于FGM结构弹塑性屈曲的研究成果，文献 [9] 用有限元法研究了受机械载荷作用的FGM梁的弹塑性屈曲。文献 [10] 用辛方法研究了轴压FGM欧拉梁的弹塑性屈曲，发现只有当幂律指数大于一定值时，才会发生弹塑性屈曲。文献 [11] 用GDQ法研究了FGM矩形板的弹塑性屈曲，发现板越厚，形变理论和增量理论的差异就越大。文献 [12] 研究了FGM板的弹塑性屈曲和后屈曲，发现弹塑性屈曲临界载荷比弹性屈曲临界载荷小得多。文献 [13] 研究了FGM杆的扭转弹塑性屈曲，发现塑性区域随着幂律指数的增加而更快地扩大。文献 [14] 研究了轴压FGM圆柱壳的弹塑性屈曲，发现随着体积分数的增加，临界载荷急剧下降。在此基础上，文献 [15] 加入了径向压力，研究了径压轴压共同作用下FGM圆柱壳的弹塑性屈曲，发现了材料的塑性流动对稳定区有显著影响。

研究FGM结构的弹塑性屈曲可更精确地预测临界载荷，从而更好地发挥材料的塑性性能。目前尚未见考虑温度依赖性的剪切可变形FGM梁的弹塑性屈曲的研究成果。因此本文考虑FGM物性参数的温度依赖性，研究FGM Timoshenko梁的弹塑性屈曲。在Hamilton体系下求解控制方程，并进行数值算例分析获得FGM梁的临界载荷和塑性变形域及其影响因素。

2. 控制方程及求解

考虑厚度方向梯度变化的矩形截面FGM梁，长为l、宽为b、高为h。在梁的几何中面上建立坐标系 $\left(x,y,z\right)$，原点O位于梁的左端横截面的中心，x轴沿轴向，该向位移记为u，几何中面上为 $u_0$ ；y轴沿宽度方向；z轴沿厚度方向，横向挠度记为w，几何中面上为 $w_0$ ；横截面的转角记为 $\phi$。弹塑性交界面为s，如图1所示。研究FGM梁在变温环境中的屈曲问题。

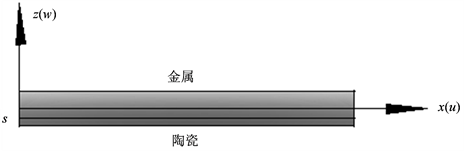
Figure 1. Functionally graded Timoshenko beam

图1. 功能梯度Timoshenko梁

2.1. 等效物性参数

FGM考虑由陶瓷和金属两相材料制成，且假设其体积分数 $V_{\text{c}}$ 和 $V_{\text{m}}$ 沿厚度方向以幂函数形式连续变化：

$V_{\text{c}}\left(z\right)={\left(\frac{h-2z}{2h}\right)}^n$, $V_{\text{m}}\left(z\right)=1-V_{\text{c}}\left(z\right)$ (1)

其中 $n\left(0\le n<\infty \right)$ 为体积分数指数，不同值代表了成分含量不同的功能梯度材料。 $n=0$ 时退化为纯陶瓷梁； $n\to \infty$ 时则为纯金属梁。对处于变温环境中的FGM梁，其材料的物性参数考虑与温度的相关性：

$P_j\left(T\right)=P_0\left(P_{-1}{T}^{-1}+1+P_{1}T+P_2{T}^2+P_3{T}^3\right)$ (2)

其中P泛指金属和陶瓷的弹性模量、切线模量和屈曲极限；j为c或m，分别代表陶瓷和金属；T为绝对温度； $P_0$、 $P_{-1}$、 $P_1$、 $P_2$、 $P_3$ 为材料的温度相关系数。弹塑性FGM的弹性模量E、切线模量H和屈服极限 ${\sigma }_{\text{Y}}$ 基于TTO模型给出：

$E=E_{\text{m}}{V}_{\text{m}}+E_{\text{c}}{V}_{\text{c}}$, $H=H_{\text{m}}{V}_{\text{m}}+E_{\text{c}}{V}_{\text{c}}$, ${\sigma }_{\text{Y}}={\sigma }_{\text{Ym}}\left(V_{\text{m}}+\frac{E_{\text{c}}}{E_{\text{m}}}{V}_{\text{c}}\right)$ (3)

其中 $E_{\text{m}}$、 $H_{\text{m}}$ 和 ${\sigma }_{\text{Ym}}$ 为金属的弹性模量、切线模量和屈曲极限； $E_{\text{c}}$ 为陶瓷的弹性模量。剪切弹性模量为 $G\left(z\right)=\frac{E\left(z\right)}{2\left(1+\mu \right)}$。泊松比 $\mu$ 随温度变化不大，一般取为常数 [16]。

2.2. 基本方程和边界条件

FGM梁的正应变 ${\epsilon }_x$ 和切应变 ${\gamma }_{xz}$ 基于Timoshenko梁理论建立：

${\epsilon }_x=\frac{\partial u_0}{\partial x}-z\frac{\partial \phi }{\partial x}$, ${\gamma }_{xz}={\gamma }_{xz}^0=\frac{\partial w_0}{\partial x}-\phi$ (4)

FGM的本构关系基于线性强化弹塑性模型建立，正应力 ${\sigma }_x$ 和切应力分别为 [16]：

${\sigma }_x=\{\begin{array}{l}E\left({\epsilon }_x-\alpha \Delta T\right)-\frac{h}{2}\le z<s\\ {\sigma }_{\text{Y}}+H\left({\epsilon }_x-\frac{{\sigma }_{\text{Y}}}{E}-\alpha \Delta T\right)s\le z\le \frac{h}{2}\end{array}$ (5a)

${\tau }_{xz}=G{\gamma }_{xz}$ (5b)

上式中 $\Delta T=T-T_0$ 为温度增量，一般初始温度 $T_0=300\text{K}$ ； $\alpha$ 为热膨胀系数，由线性混合律模型 [10] 计算；s为FGM梁的弹塑性分界面到几何中面的距离， $-\frac{h}{2}\le s\le \frac{h}{2}$。若 $s=-\frac{h}{2}$，发生弹性屈曲； $s=\frac{h}{2}$，发生塑性屈曲； $-\frac{h}{2}<s<\frac{h}{2}$，则发生弹塑性屈曲。本文考虑固定(C)和不可移简支(S)两种边界约束，边界条件分别为：

$\text{C}:u_0\text{=}{w}_0=\phi =0$, $\text{S}:u_0\text{=}{w}_0=M=0$.

2.3. 正则方程

本文利用Hamilton体系下的辛方法研究FGM梁的弹塑性屈曲。为了引入Hamilton体系，定义

$\stackrel{\dot{}}{w}=\frac{\partial w}{\partial t}$、 $w^{\prime }=\frac{\partial w}{\partial x}$ 和 $\stackrel{\dot{}}{\phi }=\frac{\partial \phi }{\partial t}$、 ${\phi }^{\prime }=\frac{\partial \phi }{\partial x}$，FGM梁的Lagrange密度函数可表示为：

$\begin{array}{l}\bar{L}=\bar{T}-\bar{V}-\bar{U}\\ \frac{1}{2}\overline{I_0}{\left(\stackrel{\dot{}}{w}\right)}^2+\frac{1}{2}\overline{I_1}{\left(\stackrel{\dot{}}{\phi }\right)}^2-\frac{1}{2}Q{\left(w^{\prime }\right)}^2\\ -\frac{1}{2}{B}_1{\left({\phi }^{\prime }\right)}^2-\frac{1}{2}{B}_2\left({\phi }^{\prime }\right)-\frac{1}{2}{B}_3{\left(w^{\prime }-\phi \right)}^2\end{array}$ (6)

其中：Q为轴向压缩荷载， $\bar{T}$ 为动能密度， $\bar{U}$ 为应变能密度， $\bar{V}$ 为势能密度， $\left({\bar{I}}_0,{\bar{I}}_1\right)={\displaystyle {\int }_{-h/2}^{h/2}\rho \left(z\right)}\left\{1,z^2\right\}\text{d}z$ 为FGM梁的单位面积的质量。 $B_1$ 和 $B_2$ 为FGM梁的刚度系数， $B_3$ 为剪切刚度系数。进行量纲为一的处理， $X=x/l$， $W=w/l$， $\varphi =h\phi /l$， $I_0=\frac{2{\bar{I}}_0{l}^4}{B_1}$， $I_1=\frac{2{\bar{I}}_1{l}^2}{B_1}$， $A_1=\frac{Q{l}^2}{B_1}$， $A_2=\frac{B_{2}l}{B_1}$， $A_3=\frac{B_3{l}^2}{B_1}$，将原变量记为 $W=q_1$， $\varphi =q_2$ 并引入对偶 $p={\left\{p_1,p_2\right\}}^{\text{T}}$，得到 $p_1=\frac{\delta L}{\delta {\stackrel{\dot{}}{q}}_1}=I_0{\stackrel{\dot{}}{q}}_1$ 和 $p_2=\frac{\delta L}{\delta {\stackrel{\dot{}}{q}}_2}=I_1{\stackrel{\dot{}}{q}}_2$，则系统的Hamilton函数表示为：

$F=p\stackrel{\dot{}}{q}-L=\frac{p_1^2}{2I_0}+\frac{p_2^2}{2I_1}+A_1{\left(W^{\prime }\right)}^2+{\left({\varphi }^{\prime }\right)}^2+A_2\left({\varphi }^{\prime }\right)+A_3{\left(W^{\prime }-\varphi \right)}^2$ (7)

通过变分运算可得FGM梁在Hamilton系统下的对偶正则方程：

$\stackrel{\dot{}}{\psi }\equiv \left\{\begin{array}{c}\frac{\delta F}{\delta p}\\ -\frac{\delta F}{\delta q}\end{array}\right\}=\left\{\begin{array}{c}\frac{p_1}{I_0}\\ \frac{p_2}{I_1}\\ \left(A_1+A_3\right)\frac{{\partial }^2{q}_1}{\partial x^2}-A_3\frac{\partial q_2}{\partial x}\\ \frac{{\partial }^2{q}_2}{\partial x^2}+A_3\left(\frac{\partial q_1}{\partial x}-q_2\right)\end{array}\right\}$ (8)

2.4. 方程的解析解

在辛空间中，FGM梁屈曲时满足条件 $\stackrel{\dot{}}{\psi }=0$，可得方程：

$\left(A_1+A_3\right)\frac{{\partial }^2{q}_1}{\partial x^2}-A_3\frac{\partial q_2}{\partial x}=0$ (9a)

$\frac{{\partial }^2{q}_2}{\partial x^2}+A_3\left(\frac{\partial q_1}{\partial x}-q_2\right)=0$ (9b)

联立求解以上方程组可得到FGM梁屈曲的挠度通解为：

$W=C\left[C_1+C_{2}x-\frac{C_3\cos \left(\sqrt{\theta }x\right)}{\theta }-\frac{C_4\sin \left(\sqrt{\theta }x\right)}{\theta }\right]$ (10)

其中 $C=\frac{A_3}{\left(A_1+A_3\right)}$，待定系数 $C_1$、 $C_2$、 $C_3$ 和 $C_4$ 由边界条件确定，本文考虑两种边界条件梁，分别是两

端固定(C-C)和一端固定一端不可移简支(C-S)。把两种边界条件分别代入到通解式(10)中得线性方程组，并化简可得分叉条件，C-C边界为：

$2-2\cos \sqrt{\theta }-\sqrt{\theta }\sin \sqrt{\theta }=0$ (11a)

C-S边界为：

$-\left(\theta +1\right)\cos \sqrt{\theta }+\sqrt{\theta }\sin \sqrt{\theta }+1=0$ (11b)

分别求解方程(11a)和(11b)得到无量纲屈曲特征值 ${\theta }_i\left(i=1,2,3,\cdots \right)$。C-C边界的 ${\theta }_i\left(i=1,2,3,\cdots \right)$ 为39.47，80.76，157.91，238.72，……；C-S边界的 ${\theta }_i\left(i=1,2,3,\cdots \right)$ 为20.19，59.67，118.90，197.85，……。考虑边界条件、并同时利用归一化方法令 $C_4=1$，可得以上特征值对应的第i阶的弹塑性屈曲模态，C-C边界为：

$W_i=C\left[\frac{1-\cos \sqrt{\theta }}{\sin \sqrt{\theta }}-\sqrt{\theta }x-\frac{\sin \sqrt{\theta }x}{\theta }+\frac{\left(\cos \sqrt{\theta }-1\right)\cos \sqrt{\theta }x}{\sin \left(\sqrt{\theta }\right)\theta }\right]$ (12a)

C-S边界为：

$W_i=C\left[\tan \sqrt{\theta }-\sqrt{\theta }x-\frac{\sin \sqrt{\theta }x}{\theta }+\frac{\sin \left(\sqrt{\theta }\right)\cos \left(\sqrt{\theta }x\right)}{\cos \left(\sqrt{\theta }\right)\theta }\right]$ (12b)

FGM梁发生弹塑性屈曲，为了求解弹塑性变形的分界面到中面的距离 $s$，可利用屈服条件 $\sigma \left(s\right)={\sigma }_Y\left(s\right)$。将特征值 ${\theta }_i$ 依次回代，并通过数值解方程，可以得到临界屈曲载荷N和弹塑性交界面s。

3. 数值算例和讨论

本节将给出以上理论推导的数值算例。梁的长度取为 $l=0.5\text{m}$，长细比分别选 $L=5$ 和 $L=10$。组分材料选为陶瓷ZrO2和金属Ti-6Al-4V，两种材料的温度相关系数可见文献 [16] [17]。

3.1. 临界屈曲载荷

图2绘出了长细比 $L=5$ 时两种边界条件FGM梁的临界载荷随材料体积分数指数n的变化关系曲线。由图可见当幂指数n和环境温差增大时，FGM梁的临界载荷会逐渐减小，即FGM梁在热环境中的承受能力也逐渐减小。是因为随着幂指数n的增大，金属含量增大，FGM梁的弹性模量和抗弯刚度减小。而且对于两种边界条件下较小的n，即 $n<40$ 和 $n<15$ 时，无临界载荷，这是由于FGM梁中的陶瓷含量高而构件不发生弹塑性屈曲失效。当 $n\ge 40$ 和 $n\ge 15$ 时，FGM梁开始发生弹塑性屈曲。另外，环境温度越高临界载荷越小，若FGM梁的环境温度增加60K时，临界载荷的差值可达5%，这是由于材料在高温环境中的弹性模量和屈服强度降低，导致FGM梁的承载能力随即降低，计算发现当温差大于150 K时梁无弹塑性屈曲发生。

(a) C-C边界(Clamped-Clamped boundary) 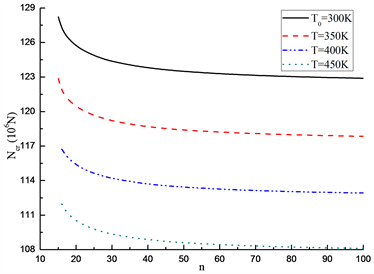(b) C-S边界(Clamped-Simply supported boundary)

Figure 2. Effect of volume fraction index n on critical load $N_{cr}$ ( $L=5$ )

图2. 体积分数指数n对临界载荷 $N_{cr}$ 的影响( $L=5$ )

(a) C-C边界(Clamped-Clamped boundary condition) 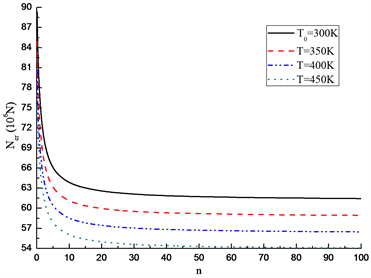(b) C-S边界(Clamped-Simply supported boundary)

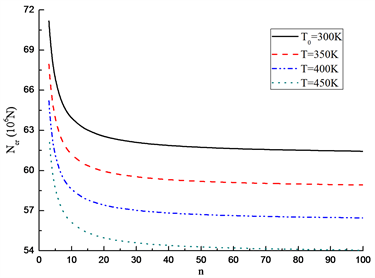
Figure 3. Effect of volume fraction index n on critical load $N_{cr}$ ( $L=10$ )

图3. 体积分数指数n对临界载荷 $N_{cr}$ 的影响( $L=10$ )

图3绘出了长细比 $L=10$ 时两种边界条件FGM梁的临界轴向载荷随材料体积分数指数n的变化关系，与图2对比可见 $L=5$ 时的临界载荷大于 $L=10$ 时的，显然长细比对临界载荷的影响较大。

3.2. 屈服界面

图4绘出了两种边界FGM梁的弹塑性分界面到中面的距离s随体积分数n的变化曲线。由图可见，当幂指数n增加时，FGM梁的弹塑性分界面的距离会逐渐增大，即逐渐远离陶瓷侧。即FGM梁发生弹塑性屈曲时，屈服界面随n的增大由陶瓷侧逐渐移向金属侧。这是由于当n增大，即金属的成分增大，FGM梁的塑性流动域逐渐减大。同时可见，当n较大时，环境温度的变化对弹塑性分界面的影响较明显。因为n较大时，FGM梁内的金属成分很大，金属的力学性能受温度的影响比陶瓷大，因此n越大，温度效应越明显。且温度越高屈服界面越靠近金属侧，塑性流动区域越大。

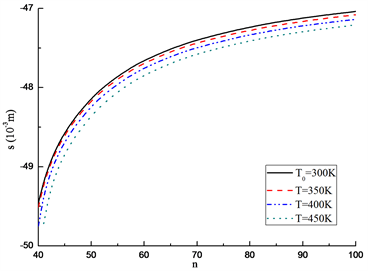(a) C-C边界(Clamped-Clamped boundary condition) 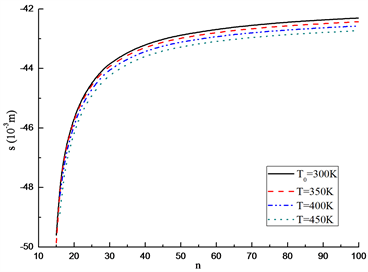(b) C-S边界(Clamped-Simply supported boundary)

Figure 4. Effect of volume fraction index n on elastoplastic interface s ( $L=5$ )

图4. 体积分数指数n对弹塑性交界面s的影响( $L=5$ )

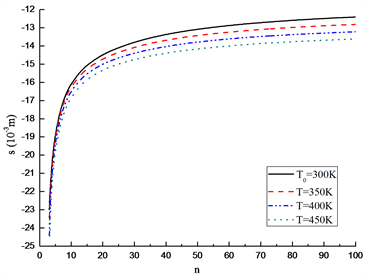(a) C-C边界(Clamped-Clamped boundary condition) (b) C-S边界(Clamped-Simply supported boundary)

Figure 5. Effect of volume fraction index n on elastoplastic interface s ( $L=10$ )

图5. 体积分数指数n对弹塑性交界面s的影响( $L=10$ )

图5绘出了长细比 $L=10$ 时两种边界FGM梁发生弹塑性屈曲时弹塑性界面到中面的距离s随体积分数n的变化规律曲线。特别地，对于C-S边界条件，当 $n<10$ 时，弹塑性分界面的距离为非单调变化，这是因为梁中金属的成分增加导致临界轴力快速减小，屈服界面向陶瓷侧移动，致使FGM梁内的塑性流动区域反而减小。

4. 结论

1) 基于Timoshenko剪切变形理论和辛方法研究了FGM梁的弹塑性屈曲，建立了Hamilton体系中的屈曲模态方程和分叉条件，通过解析求解获得了屈曲载荷和屈曲模态，同时也得到了弹塑性分界面。

2) 临界载荷随体积分数指数、环境温度和长细比的增大而减小。

3) FGM梁弹塑性屈曲时的塑性流动域受到梯度参数、长细比和边界条件的影响。对于较小长细比的FGM梁，弹塑性屈曲时屈服界面靠近陶瓷侧，塑性流动区较大；对于较大长细比的FGM梁，屈服界面更偏向金属侧，塑性流动区较小。

NOTES

^*通讯作者。