基于蠕变试验的高填方路基沉降的数值模拟

Numerical Simulation of Settlement of High Fill Roadbed Based on Creep Test

摘要: 本文主要研究了高填方路基的沉降特性，取定西至临洮高速公路某段高填方路基工程路基填土进行了一维固结蠕变试验，研究了路基填土在相同压实度、不同含水率条件下的蠕变特性，分析了含水率对路基填土蠕变特性的影响，再利用Abaqus数值软件建模分析，模拟计算了高填方路基的沉降。结果表明：路基填土含水率越大，填土变形越大，路基填土蠕变稳定的时间越长；路基填筑高度越高，填土变形越大，填土蠕变稳定的时间越长；Abaqus软件自带的Drucker-Prager塑性和蠕变耦合模型可以很好地反映各级荷载下路基填土变形与时间的变化规律，可以作为高填方路基填土的蠕变模型。

Abstract: This paper mainly studied the settlement characteristics of high-filled roadbeds. One-dimensional consolidation creep test was carried out on the high-filled roadbed engineering of a certain section of Dingxi-Lintao Expressway. The creep characteristics of subgrade fill under the same compaction degree and different moisture content conditions are studied. The influence of moisture content on the creep characteristics of subgrade fill is analyzed. Then, it uses the Abaqus numerical software modeling analysis to simulate and calculate the settlement of the high-fill roadbed. The results show: The greater the water content of the subgrade fill, the greater the deformation of the fill, and the longer the time for the creep and stability of the subgrade fill; The higher the filling height of the subgrade, the greater the deformation of the fill, and the longer the time for the fill to creep and stabilize; The Drucker-Prager plasticity and creep coupling model that comes with the Abaqus software can well reflect the changes in the deformation and time of subgrade fill under various loads, and can be used as a creep model for high fill subgrade fill.

1. 引言

随着我国“西部大开发”战略的不断推进，以及“一带一路”发展战略的实施，我国高等级公路建设逐渐由东部转向西部，由平原转入山区。公路是一个带状的线性结构物，加之西北地区地形、地质、地貌等地理条件特殊，路基两侧的山体挖方和隧道弃方较多，其大多可做高填方路基填料。由于节约土地、保护生态环境友好等特点，高填方路基在山区高速公路建设中已不可避免。与一般路基相比，高填方路基具有以下特点：第一，由于高填方路基填方量大、高度高，所以填筑时需采用分层填筑、分层压实的方法，且保证每层填土的压实质量 [1]。第二，由于高填方路基填料大多就地取材，从而填料性质复杂、级配难以控制、干湿程度不同，填筑过程中易产生不均匀沉降 [2]。第三，由于高填方路基填料的蠕变作用，高填方路基工后沉降量达到稳定需要很长时间 [3]，因而为保证高速公路的正常完工及使用，必须进行工后沉降预测和计算。高填方路基工程的沉降和稳定性问题是历来是工程领域最关注的焦点问题。路基的沉降变形是一个与荷载、时间有关的过程。土体变形的时效特性会使路基产生不可忽视的工后沉降。尤其对高路基而言，其路基底部土体在长期高应力作用下将产生过度蠕变，从而引起大量沉降并导致路基稳定性降低。

土的蠕变包括压缩蠕变、剪切蠕变、扭转蠕变、弯曲蠕变等 [4]。目前，土体蠕变模型大致分为元件蠕变模型、屈服面蠕变模型、经验蠕变模型、内时蠕变模型这4种。近年来，通过理论研究、室内试验、数值模拟等各种手段对高填方路基填土的蠕变特性开展了大量的研究。王金明 [5] 对比分析了高填方路基填料类型对不同时期沉降规律的影响。曹文贵等 [6] 基于工程监测数据，提出了高填方路基工后沉降蠕变变形的双曲线型三参数蠕变本构模型，依据有限元分析理论建立了蠕变模型参数的反演分析方法。刘宏 [7] [8] 等分别通过压缩蠕变试验和土工离心模型试验，研究了高填方路基填筑体的沉降变形。张先伟 [9] 通过直接剪切蠕变试验研究了黄石地区淤泥质土的蠕变特性。肖宏彬 [10] 等对比预压过和未预压的膨胀土的一维压缩蠕变试验结果，发现在膨胀土最优含水率附近时，预压试样的流变性状较明显，其非线性变化随着应力和时间的增长而增强。王松鹤和骆亚生 [11] 开展了杨凌地区不同干密度条件下黄土的三轴蠕变试验，建立了一种双曲线型经验蠕变模型。吴福宝 [12] 依托厦沙高速公路某高填方路堤，监测路堤工后240天的沉降量，结合有限元软件，计算出高路堤工后沉降量。Jia Liang [13] 为研究高填方路基在重力应力、车辆荷载作用下的工后沉降，对兰州至永京高速公路进行了现场监测，分析了沉降随时间和空间的演化规律。

综上所述，本文在现有文献的基础上，针对定西至临洮高速公路某段高填方路基工程路基填土进行一维固结蠕变试验，采用分别加载方式，研究相同压实度、不同含水率条件下路基填土的压缩变形与时间的变化规律。拟合一维固结蠕变试验数据，反求Abaqus软件自带的Drucker-Prager塑性和蠕变耦合模型的蠕变参数，再运用数值软件计算该段高填方路基的沉降。

2. 一维固结蠕变试验

2.1. 土样物理力学性质

土样来源于定西至临洮高速公路某段高填方路基工程路基填土，土样颜色呈黄褐色，无特殊气味。按照《公路土工试验规程》(JTG 3430-2020)，对路基填土进行了土样矿物成分分析试验、界限含水率试验、击实试验、三轴压缩试验等土工试验，获得了填土的物理力学参数，见表1。

Table 1. Physical and mechanical properties of soil samples

表1. 土样物理力学性质

2.2. 试样制备

① 风干过筛：将土样碾散，测定碾散土样的含水率，将其风干后过2 mm筛。

② 计算：测定风干含水率，按照试验方案要求计算不同含水率试样的加水量。

③ 配土：将风干称量好的土样放置在不吸水的容器中，用喷壶均匀喷洒计算好的加水量并搅拌均匀，将湿土装入塑料袋密封，标以标签，放入保湿容器内静置24 h备用，使试样水分均匀分布。

④ 取土：测定配置好的湿土的含水率，按照单个试样所需湿土质量取土；

⑤ 制作试样：环刀尺寸为f = 61.2 mm，h = 20 mm，制样仪器采用环刀制样器，根据高速公路路基的压实度控制压实标椎，此次试验试样的压实度94%。将湿土均匀分成三份，分层压实，之后将试样两端用刮土刀刮平。试样制好后，用保鲜膜包裹(保持含水率不变)，标以标签，再将包裹好的试样放入保湿容器内，试样制备完成。

2.3. 试验方法

本试验采用Ｇ型单杠杆轻便固结仪，可以同时对6个试样进行试验，试验数据人工采集。每台固结仪包括：固结装置、加压装置(可施加12.5~1600 kPa垂直压力)、变形量测装置(电子百分表，量程20 mm，最小刻度0.01 mm)；还包括环刀制样器、电子秤、刮土刀、凡士林、滤纸等其他试验用品。

本文研究含水率对路基填土蠕变特性的影响，试样压实度k = 94%，含水率w = 8%，11%，14%，17%，20%。采用分别加载的加载方式，荷载依次为100 kPa、200 kPa、400 kPa、600 kPa、800 kPa、1000 kPa。开展对相同压实度、不同含水率的试样分别施加不同荷载，记录数据，处理分析。当测得试样数据连续48 h总变形量小于0.01 mm或加载后每级恒定荷载持荷14 d时视为稳定，为防止试验过程中，试样含水率变化，在固结装置上方用保鲜膜包裹。

2.4. 试验结果分析

2.4.1. 应变–时间关系曲线

对相同压实度k = 94%，不同含水率的路基填土进行不同竖向荷载作用下的分别固结蠕变试验，得到不同含水率时试样的竖向应变与时间的关系曲线，见图1。

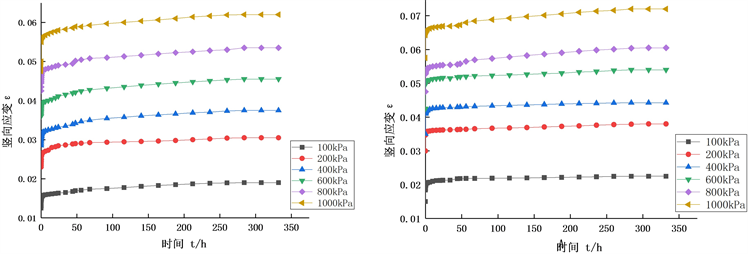(a) w = 8% (b) w = 11% 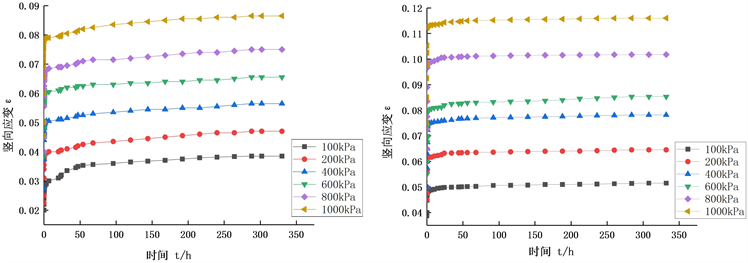(c) w = 14% (d) w = 17% 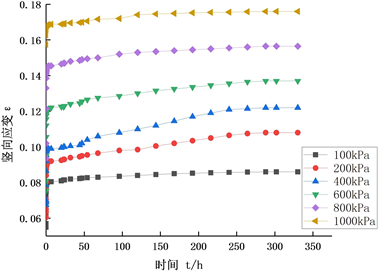(e) w = 20%

Figure 1. Strain-time curve of fills with different water content

图1. 不同含水率填土的应变-时间关系曲线

由图2可知，含水率对路基填土的蠕变变形影响较大，在相同压实度的情况下，在一定含水率范围内，当含水率越大，竖向应变越大，且竖向应变增量也越大，路基填土的蠕变变形随着含水率的增加也在增大。主要因为含水率较大时，土颗粒间距相对较大，颗粒间自由水含量较多，更容易发生相对位移，蠕变效应也更加明显。在实际高填方路基施工过程中，含水率对路基的影响较大，为减少含水率对路基沉降和稳定性的影响，应严格控制路基填土的含水率。

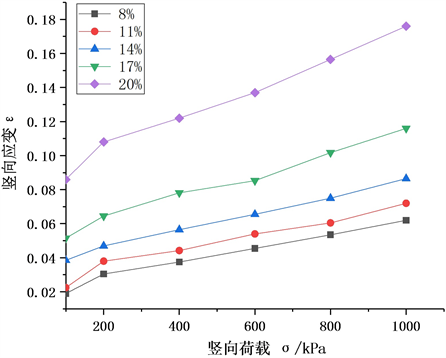
Figure2. Strain-pressure relationship curve of subgrade fill under different water content

图2. 不同含水率下路基填土应变–压力关系曲线

2.4.2. 等时曲线

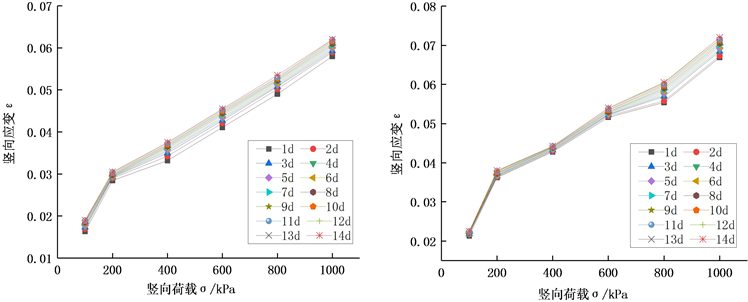
通过一维固结蠕变试验数据，可以得到不同含水率条件下试样的应力应变等时曲线，见图3。对不同含水率的试样，在不同时刻的应力应变等时曲线近似为一簇折线或者曲线，说明路基填土的蠕变变形是非线性的。含水率越高，路基填土的蠕变变形越显著。

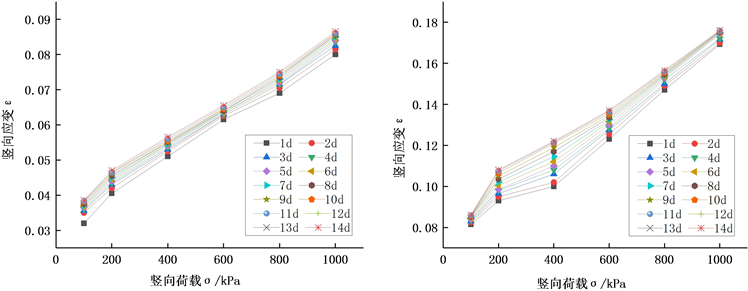(a) w = 8% (b) w = 11% (c) w = 14% (d) 10 w = 20%

Figure 3. Stress-strain isochronous curves of fills with different water content

图3. 不同含水率填土的应力-应变等时曲线

3. 蠕变模型及参数求取

3.1. 蠕变模型1) 屈服面

${\bar{\sigma }}^{cr}=\frac{q-p\tan \beta }{1-\frac{1}{3}\tan \beta }$ (1)

2) 塑性势面

$G^{cr}=\sqrt{{\left(\epsilon \bar{\sigma }{丨}_0\tan \psi \right)}^2+q^2}-p\tan \psi$ (2)

式中， $G^{\text{cr}}$ 为蠕应变率，ε为离心率参数， $\psi$ 为剪胀角， $\bar{\sigma }{丨}_0$ 为初始屈服应力。

3) 硬化规律

${\bar{\epsilon }}^{cr}=A{\left({\bar{\sigma }}^{cr}\right)}^n{t}^m$ (3)

式中， ${\bar{\epsilon }}^{\text{cr}}$ 为等效蠕变应变速率；t为荷载加载时间，A、m、n为蠕变参数。

4) 蠕变本构方程

${\bar{\epsilon }}^{\text{cr}}\text{=}\frac{A}{\text{m}+1}（{\bar{\sigma }}^{\text{cr}}{）}^{\text{n}}{\text{t}}^{\text{m+1}}$ (4)

3.2. 蠕变参数求取

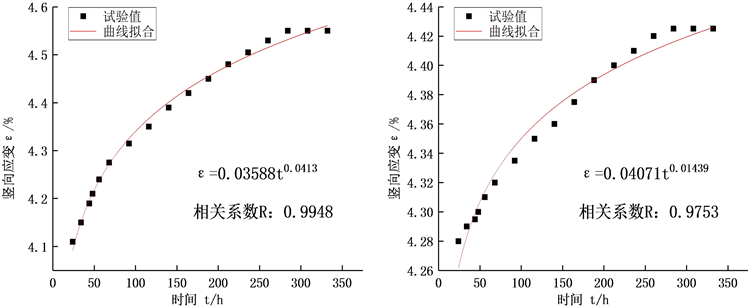
1) 蠕变参数m

由公式4可知，当加载应力一定，竖向应变和时间呈幂指数关系，拟合次固结阶段ε-t曲线，确定参数m。数据较多，在论文中只呈现部分图片，由于见图4 。

2) 蠕变参数n

由公式4可知，当加载时间一定，竖向应变和应力呈幂指数关系，拟合次固结阶段ε-σ曲线，确定参数n。数据较多，在论文中只呈现部分图片，见图5。

(a) w = 8%，竖向荷载σ = 600 kPa (b) w = 11%，竖向荷载σ = 400 kPa 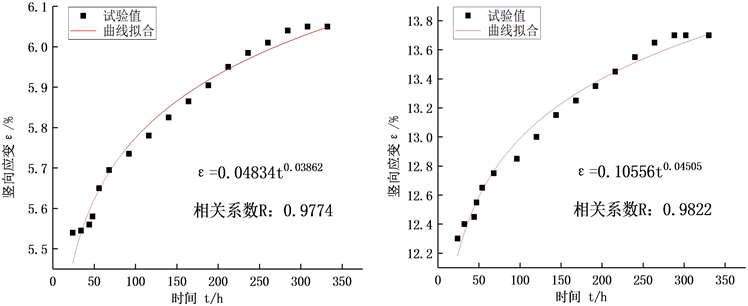(c) w = 11%，竖向荷载σ = 800 kPa (d) w = 20%，竖向荷载σ = 600 kPa

Figure 4. One-dimensional consolidation creep test fitting creep parameter m

图4. 一维固结蠕变试验拟合蠕变参数m

(a) w = 11%，加载时间为68 h (b) w = 11%，加载时间为212 h(c) w = 14%，加载时间为68 h (d) w = 14%，加载时间为212 h

Figure 5. One-dimensional consolidation creep test fitting creep parameter n

图5. 一维固结蠕变试验拟合蠕变参数n

3) 蠕变参数A

由式4可知，A的计算公式如下：

$A=a\left(m+1\right)/{\left({\bar{\sigma }}^{cr}\right)}^n$ (5)

4) 参数A、m、n计算结果见表2。

Table 2. Calculation parameters of high-fill roadbed model

表2. 高填方路基模型计算参数

由图4、图5可知，运用此蠕变模型，对不同荷载作用下路基填土的ε-t、ε-σ曲线进行拟合，精确度较高，相关系数均可达到0.95以上。这表明，此模型可以很好地描述不同荷载作用下路基填土的变形时间效应。

4. 高填方路基数值模拟

针对定西至临洮高速公路某段高填方路基工程，简化路基模型，利用Abaqus数值分析软件，结合Drucker-Prager塑性和蠕变耦合模型对高填方路基填筑体的沉降进行模拟分析。

4.1. 模型

图6为模型网格划分图，数值模型计算参数见表3，蠕变参数A、m、n见表2。路基高度为40 m，分4层，每层10 m。

Figure 6. Model meshing

图6. 模型网格划分

Table 3. Numerical model calculation parameters

表3. 数值模型计算参数

4.2. 计算结果分析

4.2.1 . 各填土层的沉降

图7为填筑土体最优含水率w = 11%时，相同断面、不同深度处沉降随时间的变化。可以看出，同断面中填方地基中心处沉降最大，随着中心线至路基两侧沉降逐渐减小。从填方第一层至第四层，路基填土沉降逐渐增大，各填土层沉降规律相同，前期直线增加，随之缓慢增长，最后趋于平稳。路基底层自重应力较小，蠕变效应也较小，单位沉降量也较小；相反，路基底层自重应力较大，随之蠕变效应较大，单位沉降量也较大，因而路基底层沉降比顶部沉降大很多。在高填方路基工程中随着路基填筑高度的增加，填筑体的沉降随之增大。

由图7可知，在填筑体最优含水率时填筑土体，路基最大沉降可以达到110.42 cm，占填方高度2.75%。填筑体顶面沉降大约需要2年才可以稳定，填筑体底面大约1.5年，沉降主要集中在填筑完工后一年。

4.2.2 . 含水率对高填方路基沉降的影响

由图8可知，高填方路基沉降先迅速增大，然后缓慢增大，最后趋于稳定。由图中可以看出，路基填土含水率不同，对应路基沉降也不同，随着含水率增大，路基沉降逐渐增大。含水率从8%变化至20%，路基沉降从迅速增长过渡至缓慢增大的时间点不同，随含水量的增大，拐点出现的时间增长，说明，路基填土含水率越大，蠕变加速阶段作用时间越长，和一维固结蠕变试验所得结论相同。含水率为8%时，沉降稳定时间为1.4年；含水率为20%时，沉降稳定时间为2.5年。分析可知，在高填方路基工程中合理控制填土含水率，一方面可以有效减小高填方路基沉降，另一方面可以缩短高填方路基工程工后沉降稳定时间。

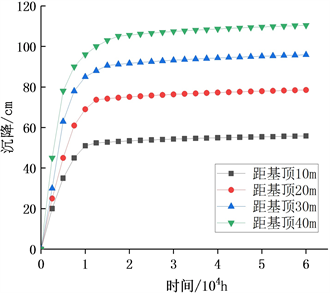
Figure 7. Settlement curves of different fill Layers of high fill roadbed

图7. 高填方路基填土不同填土层的沉降曲线

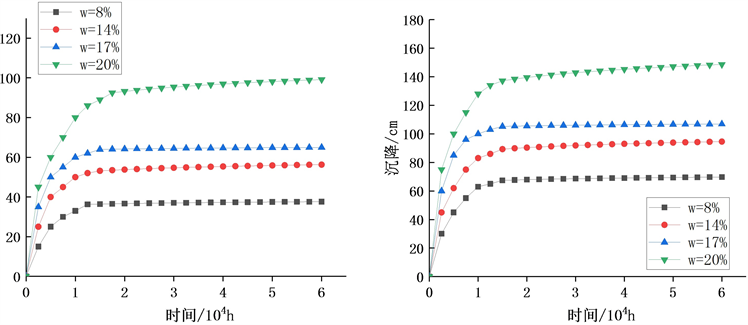(a) 距基顶10 m (b) 距基顶40 m

Figure 8. Post-construction settlement curve of high-filled roadbed under different water content

图8. 不同含水率下高填方路基工后沉降曲线

由图8中(a)可知，路基顶面含水率为8%时，工后沉降为37.64 cm；含水率为20%时，工后沉降为99.12 cm，含水率增加了12%，工后沉降增加了61.48 cm；由(b)可知，路基顶面含水率为8%时，工后沉降为69.75 cm；含水率为20%时，工后沉降为118.63 cm，含水率增加了12%，工后沉降增加了48.88 cm；不同含水率对应的路基填土工后沉降差距较大，可见含水率对路基沉降的影响至关重要。

这是由于，路基填土从8%到11%，达到最优含水率时，土颗粒间距增大，颗粒表面结合水膜变厚，颗粒间斥力增加，引力减小，压实功可以克服粒间引力，使土粒发生相对位移，趋向密实，路基压实效果较好。当填土中含水率继续增大时，虽然粒间引力减小，但土中产生了大量自由水，随着水的体积增大，颗粒所占体积就越小，在压实过程中，土孔隙里的水分大多以封闭气泡的形式存，气体不易排出，阻碍土粒移动，此时压实只能使土粒定向排列，土体体积变化微小，压实效果变差。因而，在路基填筑压实时，一定要严格控制路基填土的含水率，使其达到最佳。

5. 结论

1) 路基填土含水率对土体蠕变特性影响较大。在相同压实度、相同荷载条件下，随着含水率的增大，填土蠕变变形随之增加。说明，在高填方路基工程中严格控制填土的含水率，可以有效减小路基沉降及工后沉降，提高路基稳定性。

2) 在一维固结蠕变试验中，荷载越大，填土变形越大，蠕变稳定时间越长；含水率越大，填土变形越大，蠕变稳定时间也增大。说明随着路基填筑高度的增加，填筑体稳定所需的时间越长。

3) Abaqus软件中的Drucker-Prager塑性和蠕变耦合模型可以很好地描述此高填方路基工程中路基填土的ε-t曲线，适合作为此填筑体的蠕变模型。

参考文献